Three rods of equal length of same mentioned are joined to form an equ

Three rods of equal length of same material are joined to form an equilateral triangle ABC as shown in figure. Area of cross-section of rod AB is S, of rod BC is 2S and that of AC is S. Then match the following.
ocr_image

View Solution

Three rods of equal length of same material are joined to form an equivalent triangle $A B C$ as shown figure. Area of cross-section of rod $A B$ is $S$ of rod $B C$ is $2 S$ and that of $A C$ is $S$ , then
ocr_image
$\begin{matrix} Column-I & Column-II (A) & Temperature of junction B & (p) & Greater than 50^{\circ} C (B) & Heat current in A B & (q) & Less than 50^{\circ} C (C) & Heat current in BC & (r) & Is equal to current in BC (s) & Is \frac{2}{3} times heat current in AC (t) & None \end{matrix}$

View Solution

Match the following columns,
$\begin{matrix} Column1 & Column2 a Thermal resitance & p [MT^(-3)K^(-4)] b Stefan's constant & q [M^(-1)L^(-2)T^(3)K] c Wien's constant & r [ML^(2)T^(-3)] d Heat current & s [LK] \end{matrix}$

View Solution

Three rods of equal of length are joined to from an equilateral triangle ABC. $D$ is the midpoint of AB. The coefficient of linear expansion is $α_{1}$ for AB and $α_{2}$ for $A C$ and $B C$ . If the distance $D C$ remains constant for small changes in temperature,
ocr_image

View Solution

on heating a cylindrical metallic rod, its length increases by $2 %$ . Then area of cross section of rod will

View Solution

Three rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
ocr_image
There is no heat loss through lateral surface of the rods and temperature of ends are $T_{A} = 100^{\circ} C, T_{B} = 70^{\circ} C$ and $T_{C} = 50^{\circ} C$ . Find the temperature of junction.

View Solution

In the diagram shown in figure mass of both the balls in same. Match the following columns.
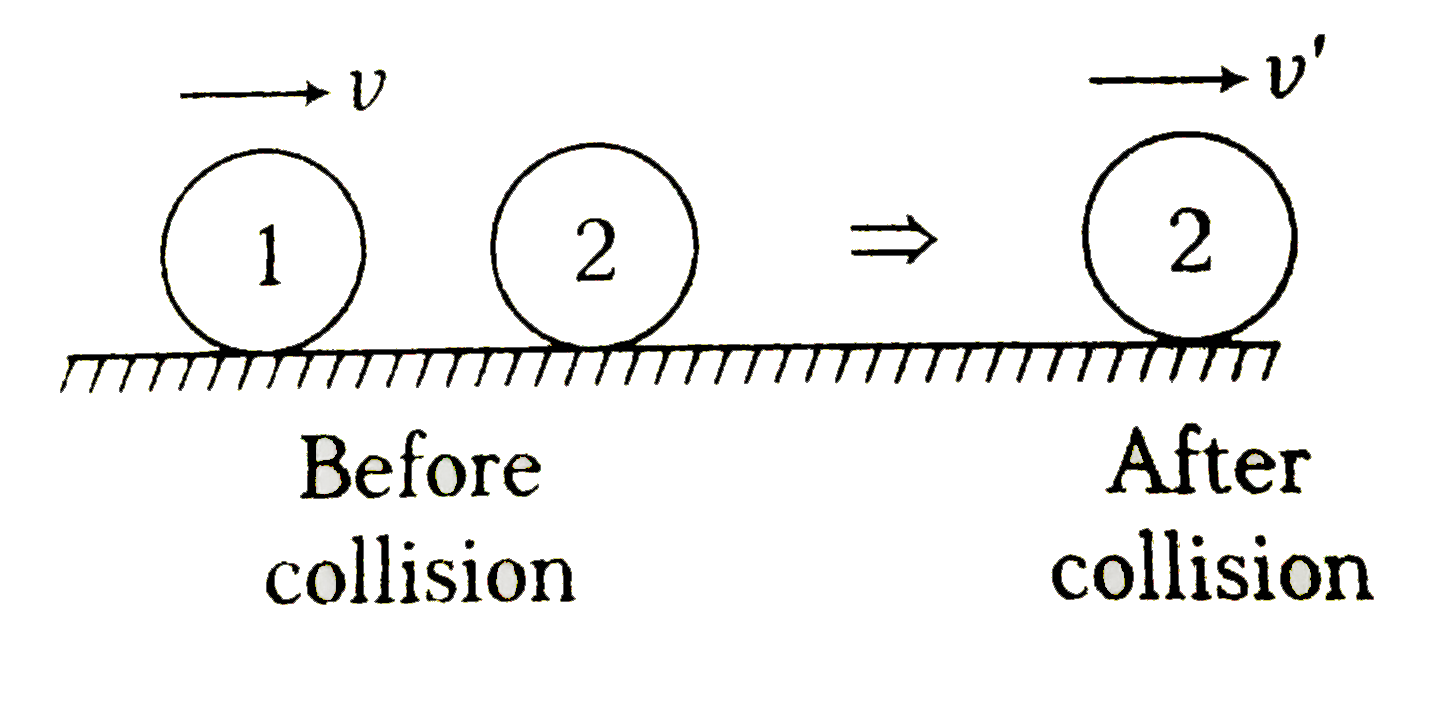
ocr_image
$\begin{matrix} Column1 & Column2 A For v^{'} = v & P e=0 B For v^{'} = v / 2 & Q e=1 C For v^{'} = 3 / 4 v & R e=1/2 - & (S data is insufficient \end{matrix}$

View Solution

Four rods of equal length $l$ and mass m each forms a square as shown in figure
Moment of inertia about three axes 1,2 and 3 are say $I_{1}, I_{2} and I_{3}$ . Then, match the following columns
ocr_image
$\begin{matrix} Column-I & Column-II (A) & I_{1} & (p) & \frac{4}{3} m l^{2} (B) & I_{2} & (q) & \frac{2}{3} m l^{2} (C) & I_{3} & (r) & \frac{1}{2} m l^{2} (s) & None \end{matrix}$

View Solution

Four rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
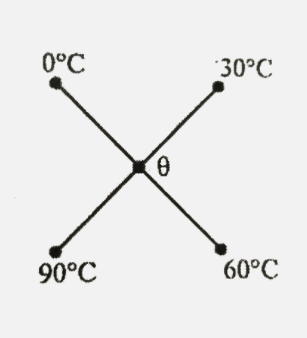
ocr_image

View Solution

Two concentric spherical shells are as shown in figure. Match the following columns
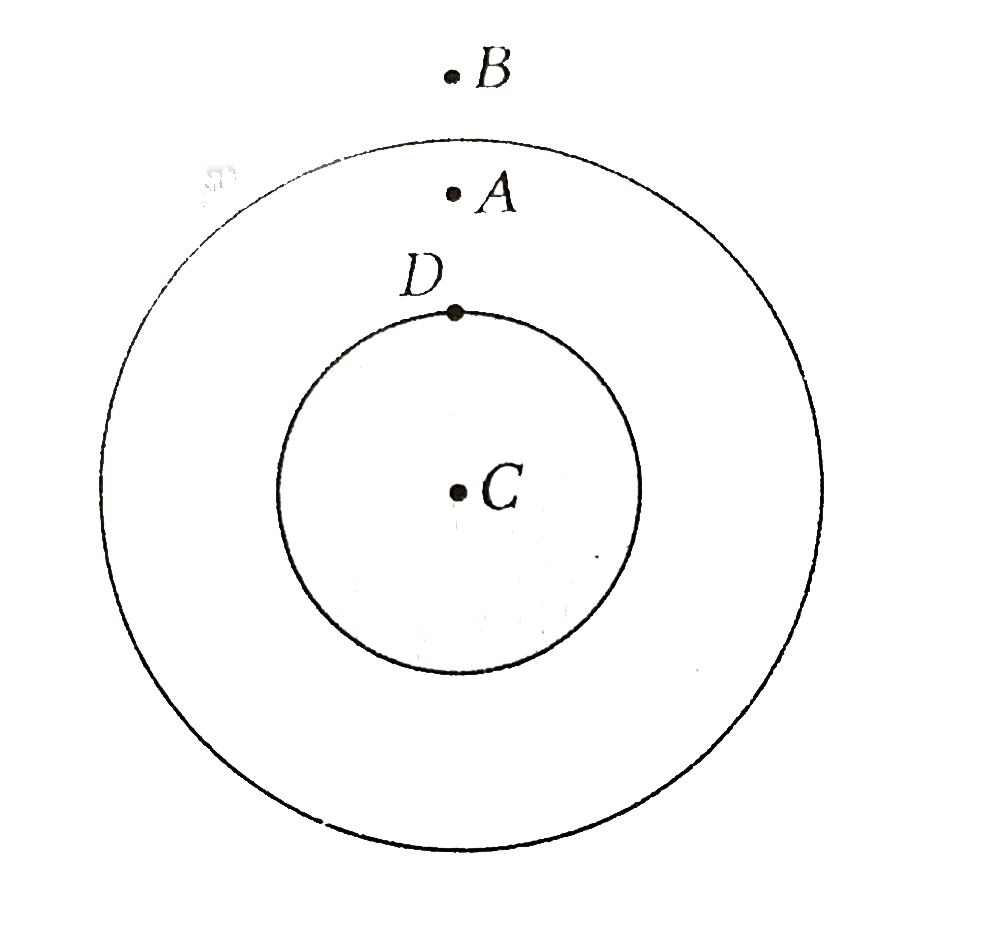
ocr_image
$\begin{matrix} Column-I & Column-II (A) & Potential at A & (p) & greater than B (B) & Gravitational field at A & (q) & less than B (C) & As one moves from C to D & (r) & Potential remains constant (D) & As one moves from D to A & (s) & Gravitational field decreases (t) & None \end{matrix}$

View Solution

Let $R_{B C} = R$ then $R_{A B} = R_{A C} = 2 R$ as $R = \frac{l}{k A}$
$\frac{100 - T_{B}}{2 R} = \frac{T_{B} - 0}{R} \Rightarrow T_{B} = {67.7}^{\circ} C$
${(\frac{Δ Q}{Δ t})}_{A B} = {(\frac{Δ Q}{Δ t})}_{B C}$ and ${(\frac{Δ Q}{Δ t})}_{A B} = \frac{2}{3} {(\frac{Δ Q}{Δ t})}_{A C}$

Topper's Solved these Questions

Similar Questions

ALLEN-GEOMETRICAL OPTICS-EXERCISE -03

Let RBC=R then RAB=RAC=2R as R=lkA 100−TB2R=TB−0R⇒TB=67.7∘C (ΔQΔt)AB=(ΔQΔt)BC and (ΔQΔt)AB=23(ΔQΔt)AC

Topper's Solved these Questions

Similar Questions

ALLEN-GEOMETRICAL OPTICS-EXERCISE -03

Let $R_{B C} = R$ then $R_{A B} = R_{A C} = 2 R$ as $R = \frac{l}{k A}$
$\frac{100 - T_{B}}{2 R} = \frac{T_{B} - 0}{R} \Rightarrow T_{B} = {67.7}^{\circ} C$
${(\frac{Δ Q}{Δ t})}_{A B} = {(\frac{Δ Q}{Δ t})}_{B C}$ and ${(\frac{Δ Q}{Δ t})}_{A B} = \frac{2}{3} {(\frac{Δ Q}{Δ t})}_{A C}$