Passage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
Now the value of k, the force constant is increased, then the maximum amplitude calcualted in above question will
remain same
increase
decrease
data in insufficient
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the force constant k and the maximum amplitude A in a simple harmonic motion (SHM) system, particularly in the context of a spring-block system on a rough surface.
1. Understanding the System:
- We have a spring with a force constant k and a mass m resting on a rough surface. The frictional force is given by Ffriction=μN, where N is the normal force.
2. Equilibrium Condition:
- At equilibrium, the spring force Fspring=kΔx (where Δx is the displacement from the equilibrium position) is balanced by the maximum frictional force. Thus, we have:
kΔx=μN
3. Effect of Increasing k:
- If the force constant k is increased, the spring force Fspring for a given displacement Δx will also increase. This means that the system can exert a greater force for the same displacement.
4. Acceleration in SHM:
- The maximum acceleration amax in SHM is given by:
amax=ω2A
- Where ω=√km. If k increases, ω increases, leading to an increase in maximum acceleration.
5. Relation to Amplitude:
- Since the net force acting on the block increases with an increase in k, the block will be displaced further from its mean position when pulled. This means that the maximum amplitude A will also increase.
6. Conclusion:
- Therefore, if the value of k (the force constant) is increased, the maximum amplitude A will also increase.
Final Answer:
If the value of k is increased, then the maximum amplitude calculated will increase.
- We have a spring with a force constant k and a mass m resting on a rough surface. The frictional force is given by Ffriction=μN, where N is the normal force.
- At equilibrium, the spring force Fspring=kΔx (where Δx is the displacement from the equilibrium position) is balanced by the maximum frictional force. Thus, we have:
kΔx=μN
- If the force constant k is increased, the spring force Fspring for a given displacement Δx will also increase. This means that the system can exert a greater force for the same displacement.
- The maximum acceleration amax in SHM is given by:
amax=ω2A
- Where ω=√km. If k increases, ω increases, leading to an increase in maximum acceleration.
- Since the net force acting on the block increases with an increase in k, the block will be displaced further from its mean position when pulled. This means that the maximum amplitude A will also increase.
- Therefore, if the value of k (the force constant) is increased, the maximum amplitude A will also increase.
If the value of k is increased, then the maximum amplitude calculated will increase.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (2)
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (3)
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Asseration & Reason
7 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Passage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
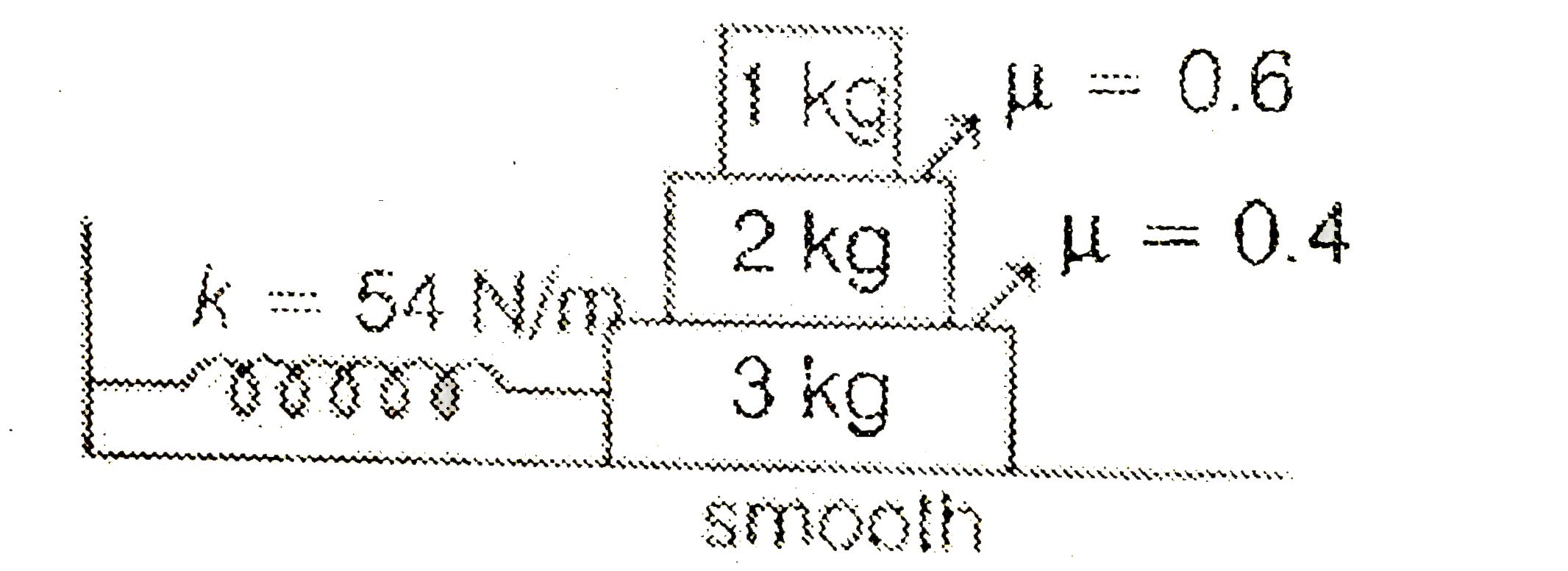
In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks?
View SolutionTwo particles are in SHM with the same amplitude and frequency along the same line and about the same point. If the maximum separation between them is √3 times their amplitude, the phase difference between them is 2πn. Find value of n
View SolutionA horizontal force applied on a body on a rough horizontal surface produces an acceleration 'a'. If coefficient of friction between the body & surface which is m is reduced to m/3, the accele-ration increases by 2 units. The value of m is
View SolutionA particle of mass 2 kg executing SHM has amplitude 10 cm and time period is 1 s.Find (i) the angular frequency (ii) the maximum speed (ii) the maximum acceleration (iv) the maximum restoring force (v) the speed when the displacement from the mean position is 8 cm (vi) the speed after 112 s the particle was at the extreme position (vii) the time taken by the particle to go directly from its mean position to half the amplitude (viii) the time taken by the particle to go directly from its exterme position to half the amplitude.
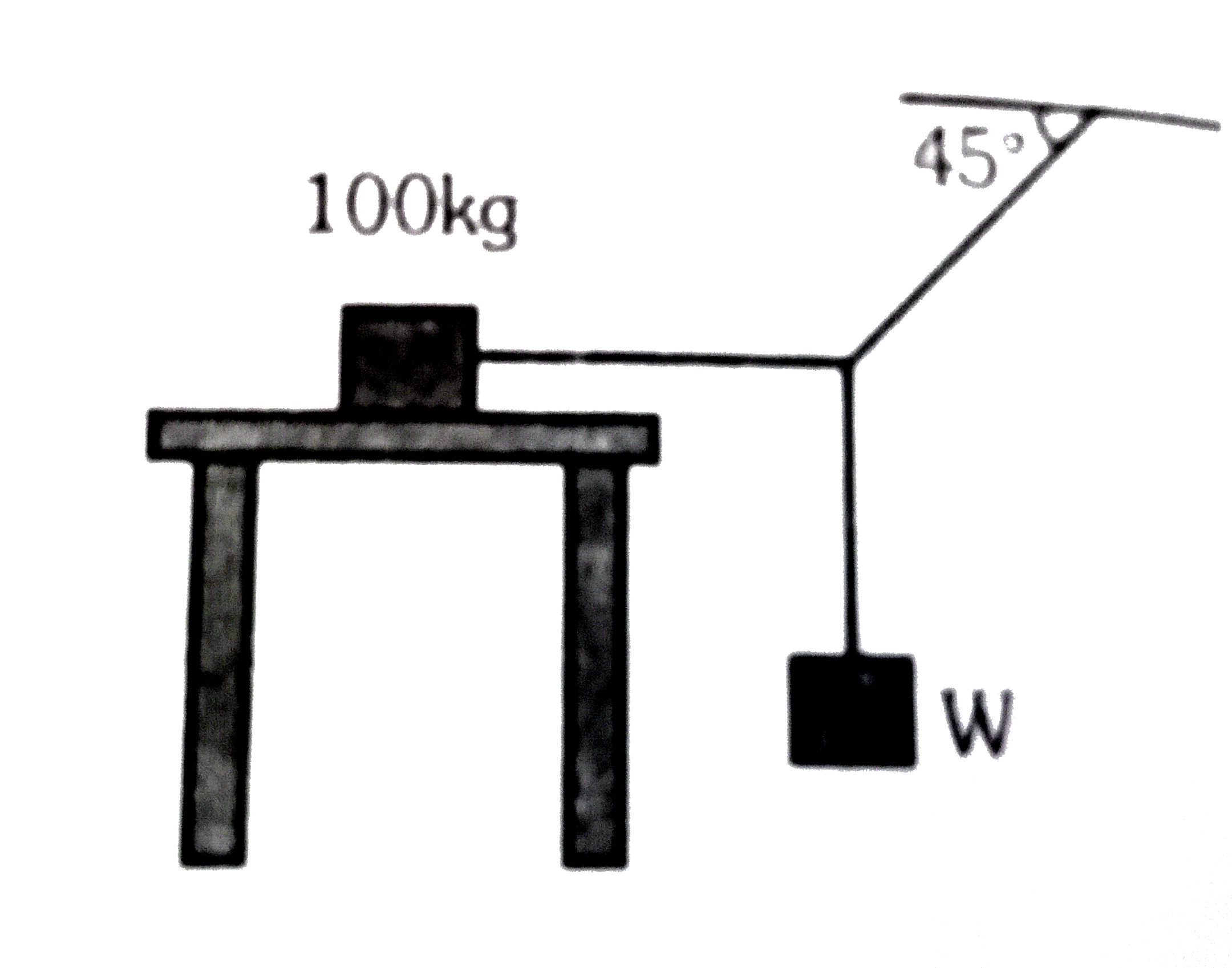
View SolutionThe system shown in the figure is in equilibrium The maximum value of W, so that the maximum value of static frictional force on 100kg. body is 450N, will be:
View SolutionThe angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
View SolutionPassage V) In SHM displacement, velocity and acceleration all oscillate simple harmonically with same angular frequency ω. Phase difference between any two is π2 except that between displacement and acceleration which is π.
v-t graph of a particle is SHM is as shown in figure Choose the wrong option.

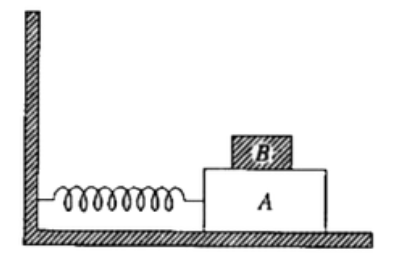
View SolutionIn Fig. A is a large block which executes shm by sliding across a frictionless surface with a frequency n. The block B is at rest on the surface of the block μs The coefficient of static friction between the two is H. Find the maximum amplitude of oscillation of the system so that the block B does not slip.
View SolutionA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the fractional loss in kinetic energy. i.e. △K/Ki
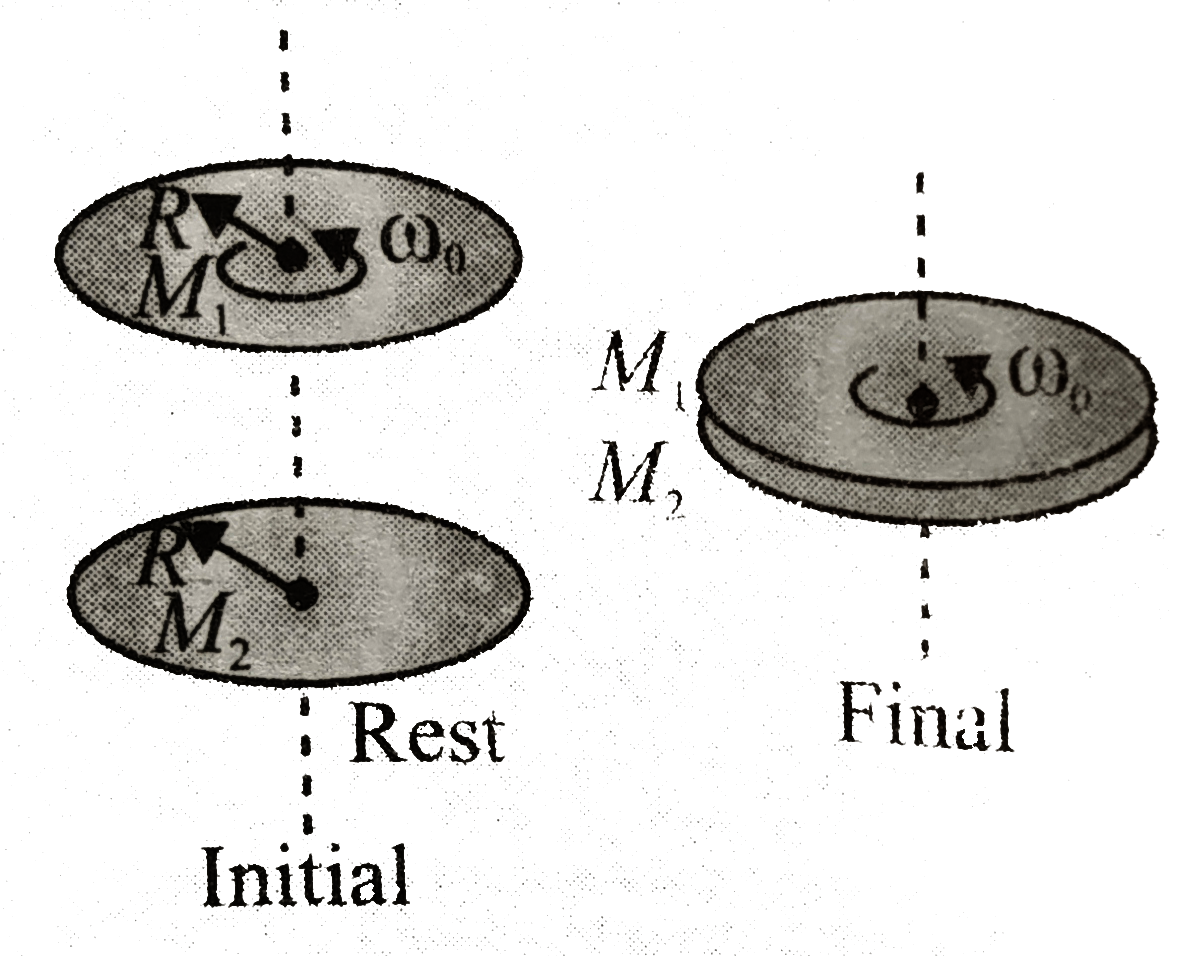
View Solution
Now when the surface is smooth , the toy car travels larger distance.
It is found that friction is caused by interlocking of irregularities on the two surfaces in contact .
Irregularities between two surfaces in contact.
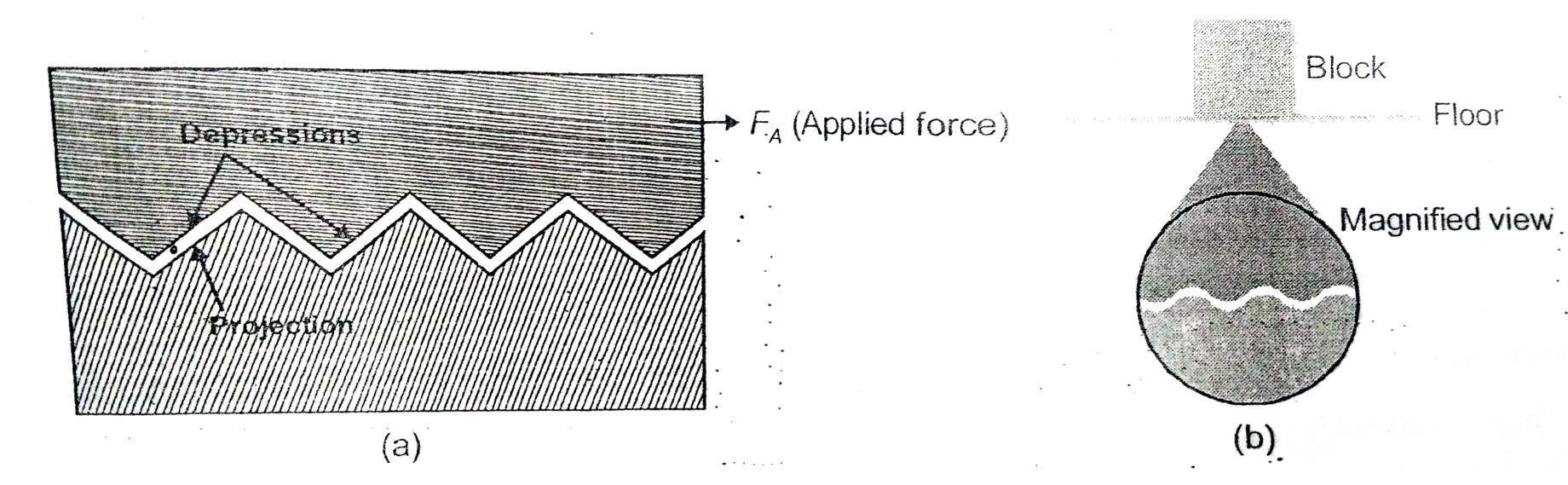
The above figure shows minute irregularities on two surfaces which are locked into one another . If we want to move any surface , some part of the external force applied is used to overcome this interlocking want to maove any surface , some part of the external force applied is used to overcome this interlocking .
A rough surface has a large number of irregularities , so the force of friction is greater .
A smooth surface has small number of irregularities , so the force of friction is less.
2. Normal reaction : The force of friction depends on the normal reaction also. As the normal reaction increases , the interlocking between two surfaces in contact increases as they press harder against each other and hence friction increases .
View Solution
