A horizontal force applied on a body on a rough horizontal surface produces an acceleration 'a'. If coefficient of friction between the body & surface which is m is reduced to m/3, the accele-ration increases by 2 units. The value of m is
2/3kg
3/2kg
3/g
1/g
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the body and use Newton's second law of motion.
Step 1: Understand the forces acting on the body
When a horizontal force F is applied to a body on a rough surface, the frictional force f opposes the motion. The frictional force can be expressed as:
f=μN
where μ is the coefficient of friction and N is the normal force. For a horizontal surface, N=mg, where m is the mass of the body and g is the acceleration due to gravity.
Step 2: Set up the equations for the two cases
1. Case 1: When the coefficient of friction is μ=m, the acceleration a is given by:
F−f=ma
Substituting for f:
F−μmg=ma(1)
2. Case 2: When the coefficient of friction is reduced to μ=m3, the new acceleration becomes a+2:
F−f′=m(a+2)
where f′=m3mg:
F−m3mg=m(a+2)(2)
Step 3: Rearranging the equations
From equation (1):
F=ma+μmg
From equation (2):
F=m(a+2)+m3mg
Step 4: Equate the two expressions for F
Setting the two expressions for F equal to each other:
ma+μmg=m(a+2)+m3mg
Step 5: Substitute μ and simplify
Substituting μ=m:
ma+m⋅mg=m(a+2)+m3mg
This simplifies to:
ma+m2g=ma+2m+m3g
Cancelling ma from both sides:
m2g=2m+m3g
Step 6: Combine like terms
Rearranging gives:
m2g−m3g=2m
Factoring out g:
g(m2−m3)=2m
Step 7: Solve for m
Dividing through by m (assuming m≠0):
g(m−13)=2
Rearranging gives:
m−13=2g
Thus:
m=2g+13
Step 8: Find a common denominator and simplify
To combine the fractions:
m=63g+13=6+1g3g
Thus:
m=6+g3g
Final Answer
To find the specific value of m, we can substitute g with 9.8m/s2 or leave it in terms of g for a general solution.
When a horizontal force F is applied to a body on a rough surface, the frictional force f opposes the motion. The frictional force can be expressed as:
f=μN
where μ is the coefficient of friction and N is the normal force. For a horizontal surface, N=mg, where m is the mass of the body and g is the acceleration due to gravity.
1. Case 1: When the coefficient of friction is μ=m, the acceleration a is given by:
F−f=ma
Substituting for f:
F−μmg=ma(1)
F−f′=m(a+2)
where f′=m3mg:
F−m3mg=m(a+2)(2)
From equation (1):
F=ma+μmg
From equation (2):
F=m(a+2)+m3mg
Setting the two expressions for F equal to each other:
ma+μmg=m(a+2)+m3mg
Substituting μ=m:
ma+m⋅mg=m(a+2)+m3mg
This simplifies to:
ma+m2g=ma+2m+m3g
Cancelling ma from both sides:
m2g=2m+m3g
Rearranging gives:
m2g−m3g=2m
Factoring out g:
g(m2−m3)=2m
Dividing through by m (assuming m≠0):
g(m−13)=2
Rearranging gives:
m−13=2g
Thus:
m=2g+13
To combine the fractions:
m=63g+13=6+1g3g
Thus:
m=6+g3g
To find the specific value of m, we can substitute g with 9.8m/s2 or leave it in terms of g for a general solution.
Similar Questions
A block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View Solution
Knowledge Check
Two blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
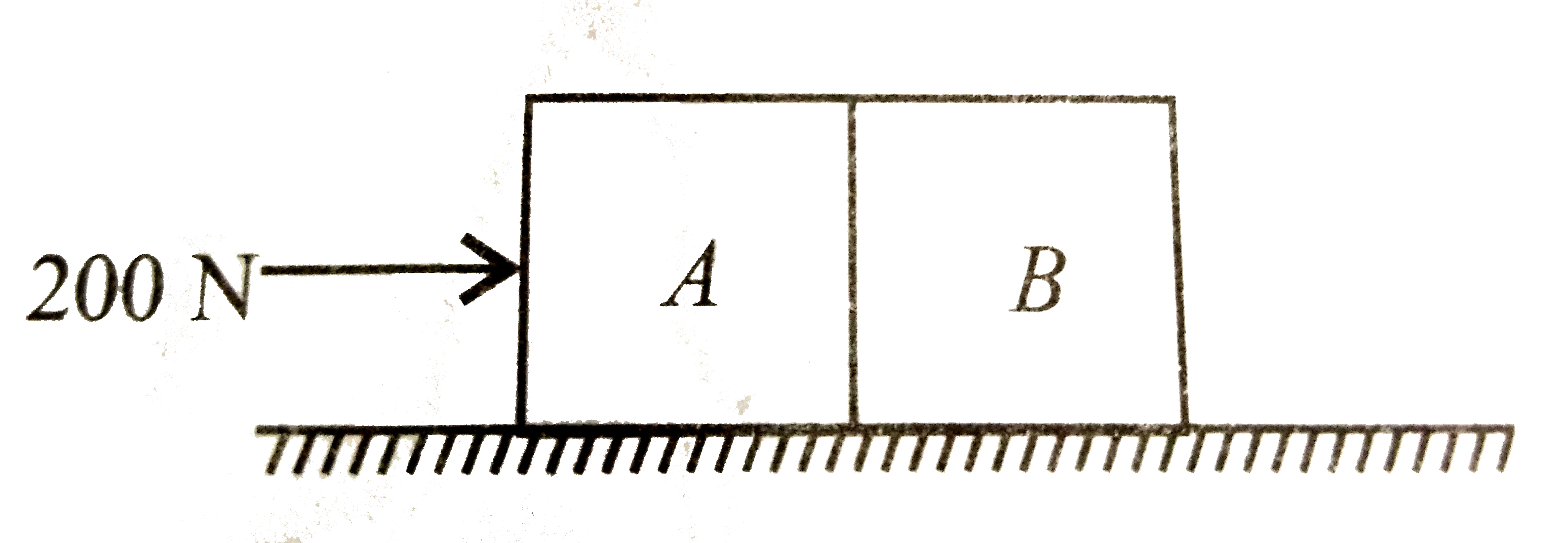 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
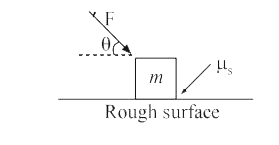
What is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
View SolutionIf a body has kinetic energy. T, moving on a rough horizontal surface stops at distance y. The frictional force exerted on the body is
View SolutionA body of mass 5kg is under the action of 50N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 3 s is
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
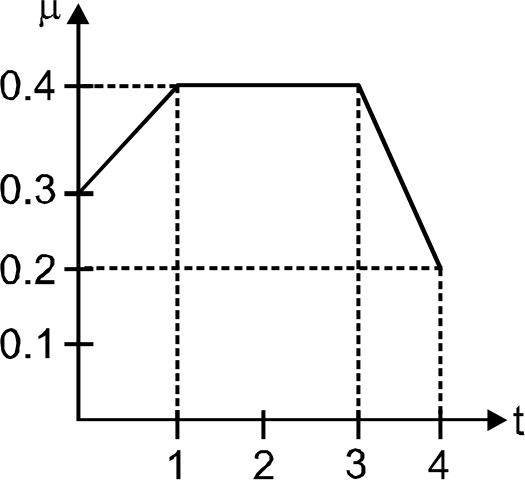
View SolutionA small body is projected with a velocity of 20.5ms−1 along rough horizontal surface. The coefficient of friction (μ) between the body and surface changes with time t (in s) as the the body moves along the surface. Find the velocity at the end of 4s in m/s
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
View Solution
