Calculate the time period of a uniform square plate of side 'a' if it is suspended through a corner.
The correct Answer is:A, B, C
To calculate the time period of a uniform square plate of side 'a' suspended through a corner, we can follow these steps:
Step 1: Determine the Moment of Inertia
The moment of inertia (I) of a square plate about its center of mass (CM) is given by the formula:
ICM=ma26
where m is the mass of the plate and a is the side length.
Since the plate is suspended from a corner, we need to use the parallel axis theorem to find the moment of inertia about the corner. The distance from the center of mass to the corner is a√2.
Using the parallel axis theorem:
I=ICM+md2
where d=a√2.
Substituting the values:
I=ma26+m(a√2)2
I=ma26+ma22
I=ma26+3ma26
I=4ma26=2ma23
Step 2: Calculate the Torque
When the plate is displaced by an angle θ, the torque (τ) due to gravity acting on the center of mass is given by:
τ=mg⋅(perpendicular distance)
The perpendicular distance from the line of action of the weight to the pivot point (corner) is:
Perpendicular distance=a√2⋅θ
Thus, the torque can be expressed as:
τ=mg⋅(a√2⋅θ)
Step 3: Relate Torque to Angular Acceleration
According to Newton's second law for rotation:
τ=Iα
where α is the angular acceleration. Since α=d2θdt2, we can write:
mg⋅(a√2⋅θ)=Id2θdt2
Step 4: Substitute Moment of Inertia
Substituting the moment of inertia we found earlier:
mg⋅(a√2⋅θ)=2ma23d2θdt2
Step 5: Rearranging the Equation
Rearranging gives:
d2θdt2+3g2aθ=0
This is a simple harmonic motion equation of the form:
d2θdt2+ω2θ=0
where ω2=3g2a.
Step 6: Calculate the Time Period
The angular frequency ω is related to the time period T by:
T=2π√Iτ
Substituting ω:
T=2π√2a3g
Final Result
Thus, the time period T of the uniform square plate suspended through a corner is:
T=2π√2a3g
---
The moment of inertia (I) of a square plate about its center of mass (CM) is given by the formula:
ICM=ma26
where m is the mass of the plate and a is the side length.
I=ICM+md2
where d=a√2.
I=ma26+m(a√2)2
I=ma26+ma22
I=ma26+3ma26
I=4ma26=2ma23
When the plate is displaced by an angle θ, the torque (τ) due to gravity acting on the center of mass is given by:
τ=mg⋅(perpendicular distance)
The perpendicular distance from the line of action of the weight to the pivot point (corner) is:
Perpendicular distance=a√2⋅θ
τ=mg⋅(a√2⋅θ)
According to Newton's second law for rotation:
τ=Iα
where α is the angular acceleration. Since α=d2θdt2, we can write:
mg⋅(a√2⋅θ)=Id2θdt2
Substituting the moment of inertia we found earlier:
mg⋅(a√2⋅θ)=2ma23d2θdt2
Rearranging gives:
d2θdt2+3g2aθ=0
d2θdt2+ω2θ=0
where ω2=3g2a.
The angular frequency ω is related to the time period T by:
T=2π√Iτ
Substituting ω:
T=2π√2a3g
Thus, the time period T of the uniform square plate suspended through a corner is:
T=2π√2a3g
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [B]105videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
Let l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
View SolutionLet l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
View Solution
Knowledge Check
- Question 1 - Select One
Ler l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
AIBIsin2θCIcos2θDIcos2(θ2).
Find the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.
 View Solution
View SolutionThe radius of gyration of a uniform square plate of mass M and sida about its diagonal is
View SolutionIn the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
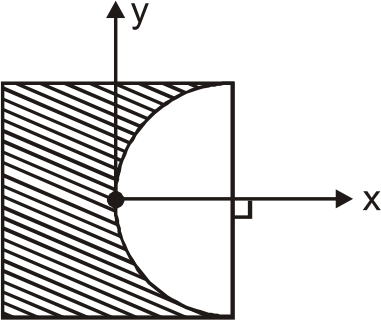 View Solution
View SolutionA square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :
 View Solution
View SolutionFind time period of uniform disc of mass m and radius r suspended through point r/2 away from centre, oscillating in a plane parallel to its plane.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View Solution

