Two springs of force constants and are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both and are made four times their original values, the frequency of oscillation becomes :Two springs of force constants and are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes :
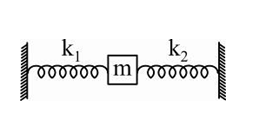
f/2
f/4
4f
2f
The correct Answer is:D
_E01_384_S01.png)
The orginal frequency of osillation
f=12π√k1+k2m
On increasing the k1 and k2 by 4 times, then f
f'=12π√(4k1k2m)=2f
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [B]
Explore 12 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:MCQ s one or more than one correct answers
Explore 5 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-04 [B]
Explore 105 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
Two springs of force constants k1 and k2, are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png)
View SolutionFrom the given figure find the frequency of oscillation of the mass m

View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
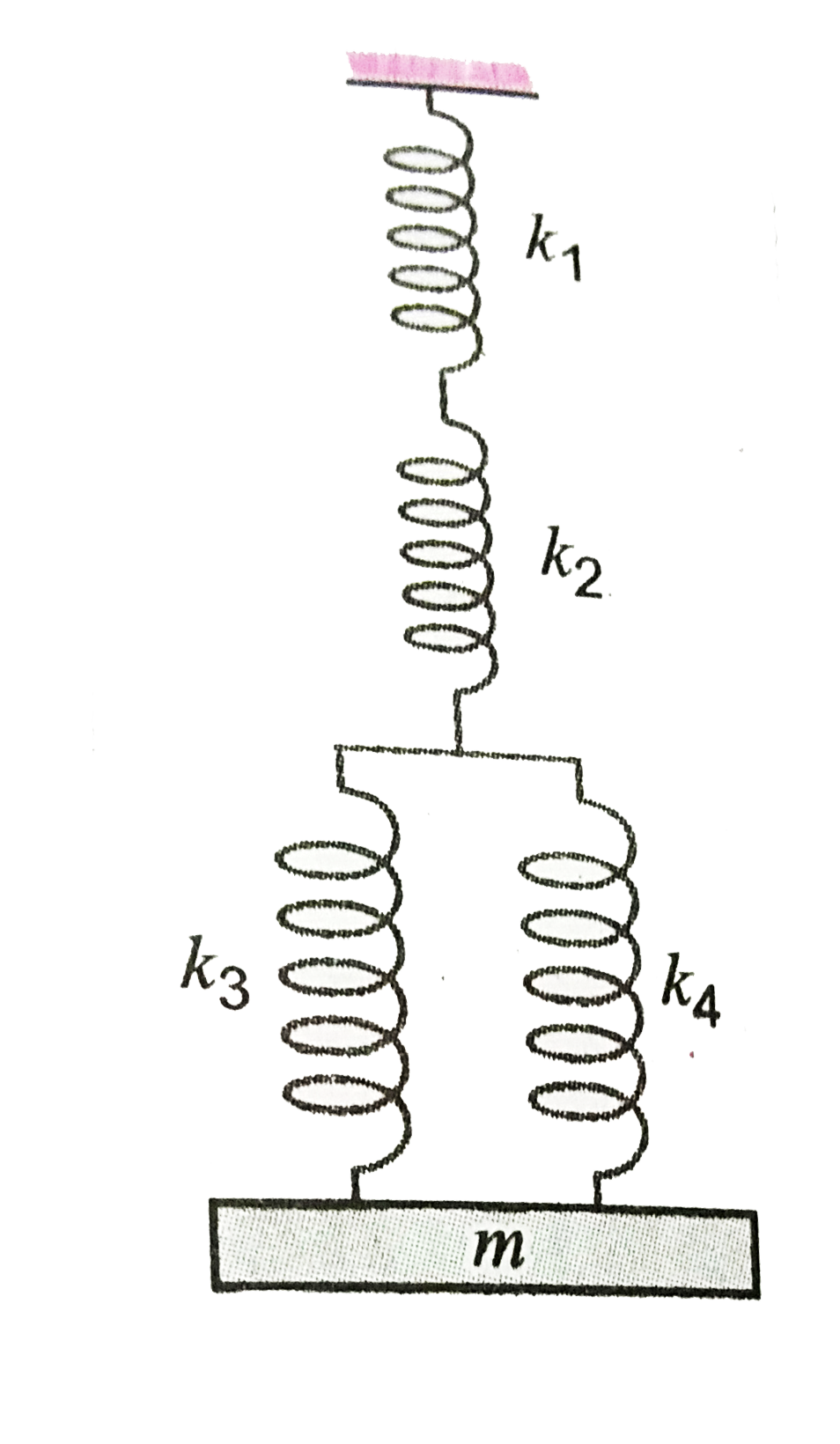 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
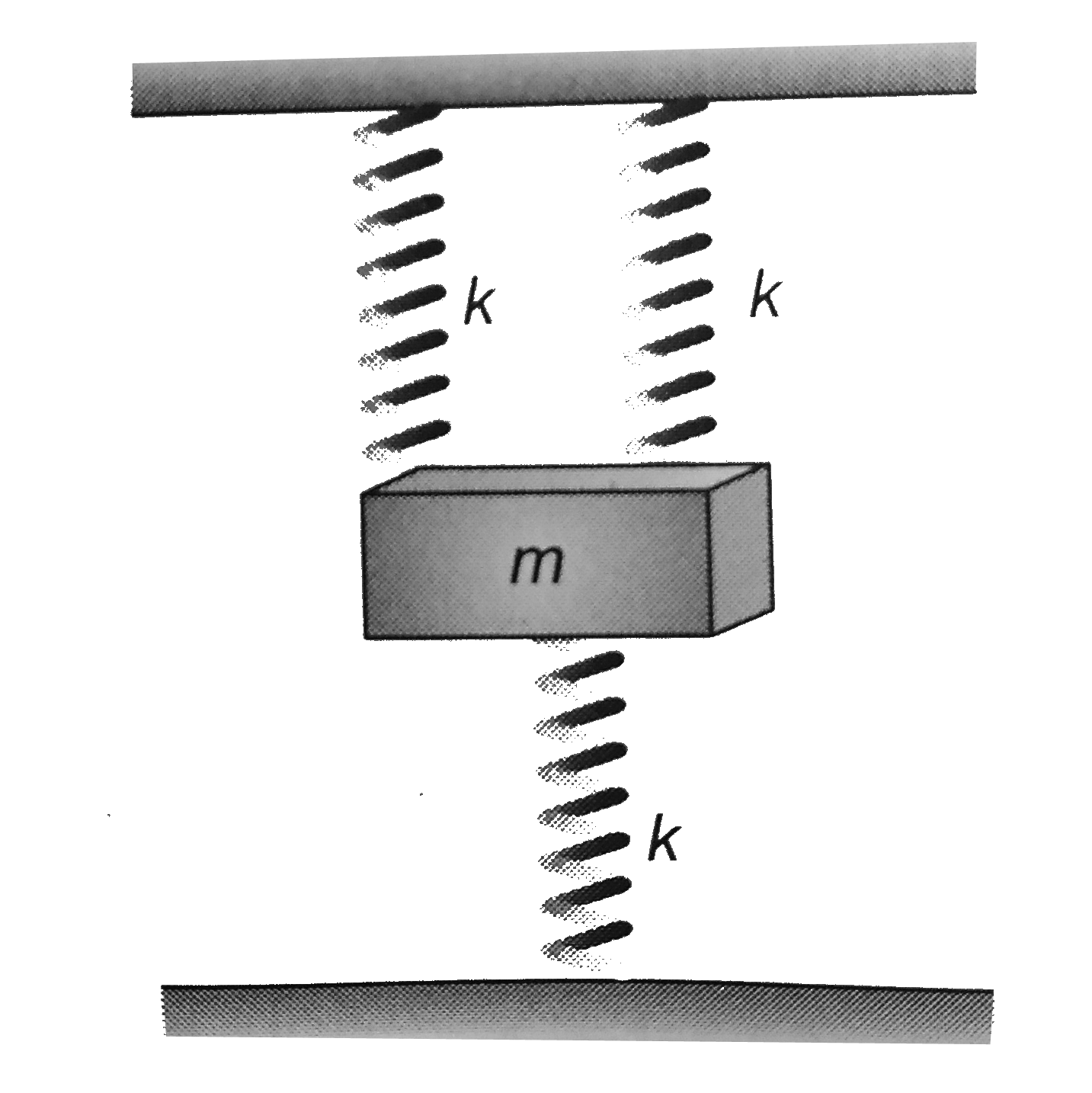
In the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionTwo springs of force constants 7Nm−1and9Nm−1 are connected in parallel and is fixed to body of mass 100 g. Find the period of oscillation.
View SolutionIf two springs of force constants 7Nm−1and9Nm−1 are connected in series and is fixed to a body of mass 100 g. Find the period of oscillation.
View SolutionA spring mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will
View SolutionFour spring connect with mass as shown in figure. Find frequency of S.H.M.

View Solution
