A bird moves from point (1,−2) to (4,2) . If the speed of the bird is 10m/sec, then find the velocity vector of the bird ?
5(ˆi−2ˆj)
5(4ˆi+2ˆj)
0.6ˆi+0.8ˆj
6ˆi+8ˆj
The correct Answer is:D
To find the velocity vector of the bird moving from point (1,−2) to (4,2) with a speed of 10m/s, we can follow these steps:
Step 1: Identify the Points
Let point A be (1,−2) and point B be (4,2).
Step 2: Calculate the Displacement Vector
The displacement vector →AB can be calculated using the formula:
→AB=(x2−x1)^i+(y2−y1)^j
where (x1,y1)=(1,−2) and (x2,y2)=(4,2).
Calculating the components:
- x2−x1=4−1=3
- y2−y1=2−(−2)=2+2=4
Thus, the displacement vector is:
→AB=3^i+4^j
Step 3: Calculate the Magnitude of the Displacement Vector
The magnitude of the displacement vector |→AB| is given by:
|→AB|=√(3)2+(4)2=√9+16=√25=5
Step 4: Calculate the Unit Vector in the Direction of Displacement
The unit vector ^AB in the direction of the displacement vector is:
^AB=→AB|→AB|=3^i+4^j5=35^i+45^j
Step 5: Calculate the Velocity Vector
The velocity vector →V is given by the product of the speed and the unit vector:
→V=speed×^AB=10×(35^i+45^j)
Calculating this gives:
→V=10×35^i+10×45^j=6^i+8^j
Final Answer
Thus, the velocity vector of the bird is:
→V=6^i+8^j
---
Let point A be (1,−2) and point B be (4,2).
The displacement vector →AB can be calculated using the formula:
→AB=(x2−x1)^i+(y2−y1)^j
where (x1,y1)=(1,−2) and (x2,y2)=(4,2).
- x2−x1=4−1=3
- y2−y1=2−(−2)=2+2=4
→AB=3^i+4^j
The magnitude of the displacement vector |→AB| is given by:
|→AB|=√(3)2+(4)2=√9+16=√25=5
The unit vector ^AB in the direction of the displacement vector is:
^AB=→AB|→AB|=3^i+4^j5=35^i+45^j
The velocity vector →V is given by the product of the speed and the unit vector:
→V=speed×^AB=10×(35^i+45^j)
Calculating this gives:
→V=10×35^i+10×45^j=6^i+8^j
Thus, the velocity vector of the bird is:
→V=6^i+8^j
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Multiple Correct Type Questions.
3 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) ComprehensionType Questions.
3 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
A bird moves from point (1m,−2m,3m) to (4m,2m,3m). If the speed of the bird is 10m/s, then the velocity vector of the bird in m/s is:
View SolutionA bird flies to and fro between two cars wich move with velocities v1 and v2, If the speed of the bird is v3 and the initial distance ofseparation between then is d, find the total distance covered bythe bird till the cars meet.
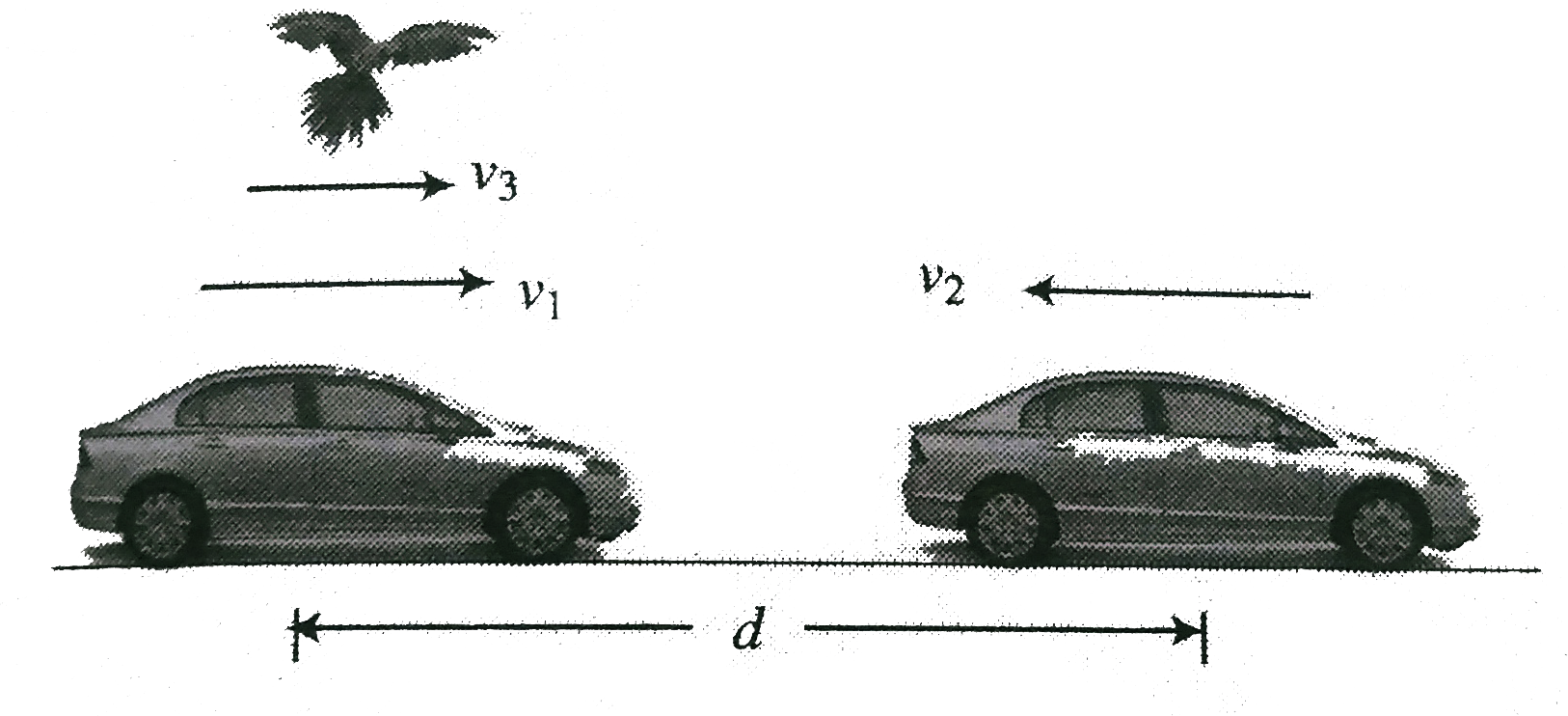 .
.
View Solution
Knowledge Check
A bird flies from (-3m, 4m, -3 m) to (7m, -2m, -3m) in the xyz-coordinates. The bird's displacement vector is given by
A(4ˆi+2ˆj−6ˆk)B(10ˆi−6ˆj)C(4ˆi−2ˆj)D(10ˆi+6ˆj−6ˆk)
A fish rising vertically to the surface of water in a lake uniformly at the rate of 3ms−1 observes a bird diving vertically towards the water at a rate of 9ms−1 vertically above it. If the refractive index of water is 4/3 the actual velocity of the dive of the bird is (in ms−1)
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionA point sourcs S is moving with a speed of 10m/s in x−y plane as shown in the figure. The radius of curvature of the concave mirror is 4m. Determine the velocity vector of the image formed by paraxial rays.
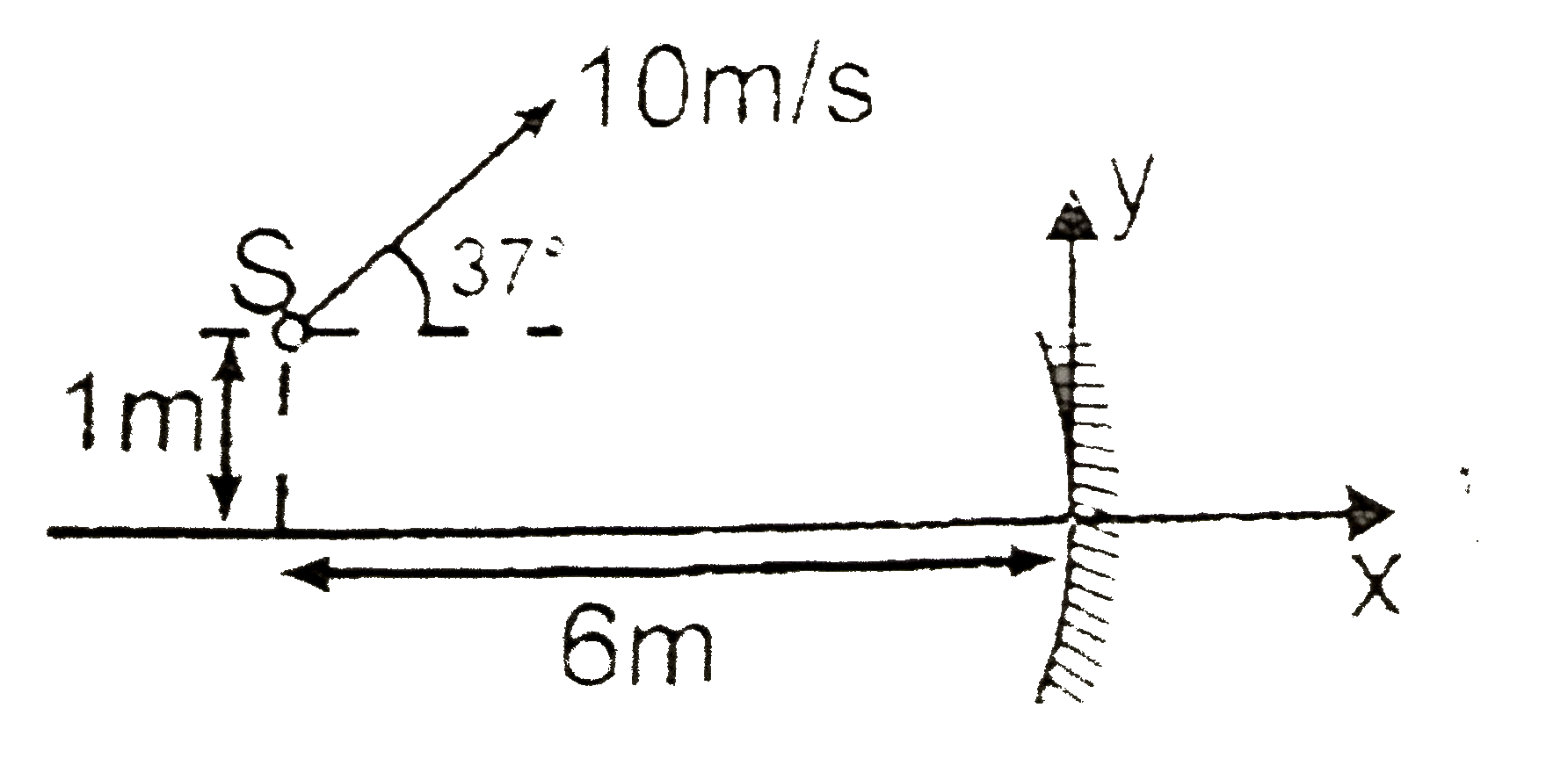
View SolutionThe escape velocity at the surface of Earth is approximately 8 km/s. What is the escape velocity for a planet whose radius is 4 times and whose mass is 100 times that of Earth?
View SolutionIf velocity of fish in upward direction is 4 m/s with respect to surface and velocity of bird in downward direction with respect to surface is 3 m/s. Then find the velocity of fish with respect to bird (Given that .aμw=43)
View SolutionOn a horizontal flat ground, a person is standing at a point A. At this point, he installs a 5m long pole vertically. Now , he moves 5m towards east and then 2m towards north and reaches at a point B. There he installs another 3m long vertical pole . A bird flies from the top of the first pole to the top of the swecond pole. Find the displacement and magnitude of the displacement of the bird.
View SolutionA car is moving in direction →r=−4ˆi+3ˆj with a speed of 10ms−1. Write the velocity vector of car in unit vector notation.
View Solution