A body placed in free space, is simultaneously acted upon by three forces −→F1,−→F2 and −→F3. The body is in equilibrium and the forces −→F1 and −→F2 are known ot be 36 N due north and 27 N due east respectively. Which of the following best describes the force −→F3?
36N due south
53N due 60∘ south of east
45N due 53∘ south of west
45N due 37∘ north of west.
The correct Answer is:C
To solve the problem, we need to find the force →F3 acting on a body that is in equilibrium, given two other forces →F1 and →F2.
1. Identify the Forces:
- →F1=36N (due North)
- →F2=27N (due East)
2. Equilibrium Condition:
- For the body to be in equilibrium, the vector sum of all forces acting on it must be zero:
→F1+→F2+→F3=0
- Rearranging gives:
→F3=−(→F1+→F2)
3. Calculate the Resultant of →F1 and →F2:
- The resultant force →R can be calculated using the Pythagorean theorem since →F1 and →F2 are perpendicular to each other:
R=√F21+F22=√(36N)2+(27N)2
- Calculating the squares:
R=√1296+729=√2025=45N
4. Direction of →F3:
- The direction of →F3 is opposite to that of the resultant →R.
- To find the angle θ that →R makes with the east direction, we use:
tan(θ)=F1F2=3627=43
- Therefore, θ=tan−1(43)≈53∘.
5. Determine the Direction of →F3:
- Since →F1 is directed north and →F2 is directed east, the resultant →R will be directed northeast at an angle of 53∘ from the east.
- Thus, →F3 will be directed opposite to this, which is 53∘ south of west.
6. Final Result:
- Therefore, the force →F3 can be described as:
→F3=45N due 53∘ south of west
Conclusion:
The force →F3 is 45N directed 53∘ south of west.
---
- →F1=36N (due North)
- →F2=27N (due East)
- For the body to be in equilibrium, the vector sum of all forces acting on it must be zero:
→F1+→F2+→F3=0
- Rearranging gives:
→F3=−(→F1+→F2)
- The resultant force →R can be calculated using the Pythagorean theorem since →F1 and →F2 are perpendicular to each other:
R=√F21+F22=√(36N)2+(27N)2
- Calculating the squares:
R=√1296+729=√2025=45N
- The direction of →F3 is opposite to that of the resultant →R.
- To find the angle θ that →R makes with the east direction, we use:
tan(θ)=F1F2=3627=43
- Therefore, θ=tan−1(43)≈53∘.
- Since →F1 is directed north and →F2 is directed east, the resultant →R will be directed northeast at an angle of 53∘ from the east.
- Thus, →F3 will be directed opposite to this, which is 53∘ south of west.
- Therefore, the force →F3 can be described as:
→F3=45N due 53∘ south of west
The force →F3 is 45N directed 53∘ south of west.
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Multiple Correct Type Questions.
3 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) ComprehensionType Questions.
3 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
A body is at rest under the action of three forces, two of which are →F1=4ˆi,→F2=6ˆj, the third force is
View SolutionA moving perticle of mass m is acted upon by five forces →F1,→F2,→F3,→F4 and →F5. Forces →F2 and →F3 are conservative and their potential energy funcations are U and W respectively. Speed of the particle changes from Va to Vb when it moves from position a to b. Choose the correct option :
View Solution
Knowledge Check
A body is moving under the action of two force −−−−−−−−−−→F1=2ˆi−5ˆj , −−−−−−−−−−→F2=3ˆi−4ˆj . Its velocity will become uniform under a third force −→F3 given by.
A5ˆi−9ˆjB−5ˆi−9ˆjC5ˆi+9ˆjD−5ˆi+9ˆjA body is moving under the action of two force −−−−−−−−−−→F1=2ˆi−5ˆj , −−−−−−−−−−→F2=3ˆi−4ˆj . Its velocity will become uniform under a third force −→F3 given by.
A5ˆi−ˆjB−5ˆi−ˆjC5ˆi+ˆjD−5ˆi+9ˆj
Two forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
View SolutionABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

View SolutionThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
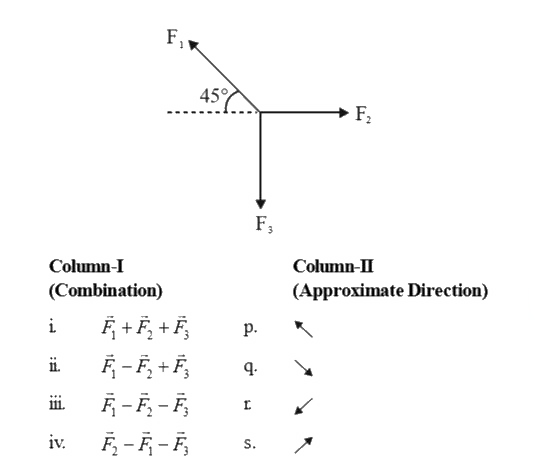
Now match the given columns and select the correct option from the codes given below.
View SolutionAn object is acted upon by the forces →F1=4ˆiN and →F2=(ˆi−ˆj)N. If the displacement of the object is D=(ˆi+6ˆj−ˆk)m, the kinetic energy of the object
View SolutionA particle of m=5kg is momentarily at rest at x=att=. It is acted upon by two forces →F1 and →F2. Vec(F)1=70ˆj N. The direction and manitude of →F2 are unknown. The particle experiences a constant acceleration, →a,in the direction as shown in (figure) Neglect gravity.
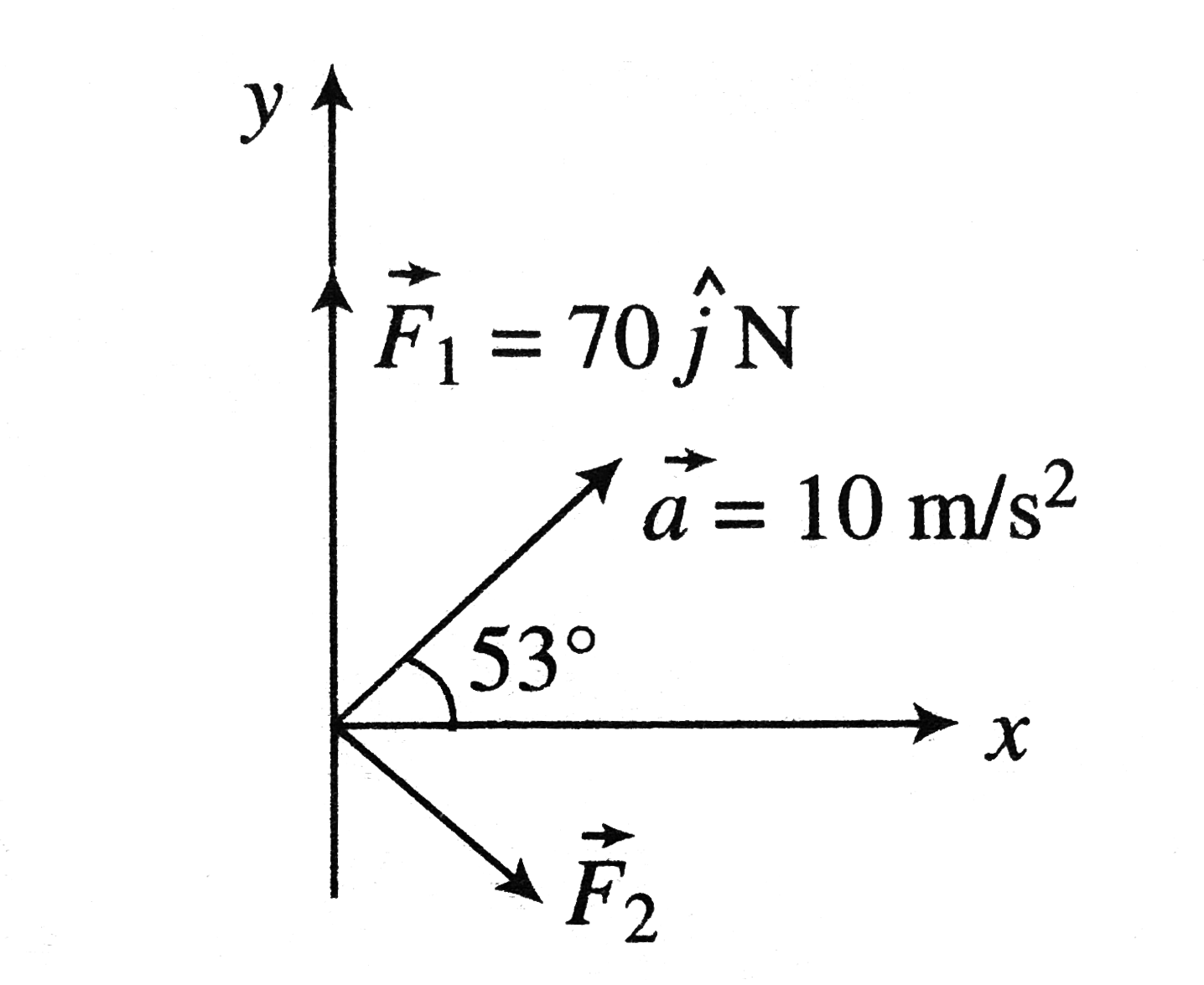
a.Find the missing force →F2.
b. What is the velocity vector of the particle at t=10s?
c. What third force, →F3 is required to make the acceleration of the particle zero? Either give magnitude and direction of →F3 or its components.
View SolutionA moving particle is acted upon by several forces F1,F2,F3….etc. One of the force is chosen sat F2 the which of the following statement about F2 will be true.
View Solution
