Just after firing, a bullet is found to move at an angle of 37∘ to the horizontal. Its acceleration is 10m/s2 downwards. Find the component of its acceleration in the direction of its velocity.
−6m/s2
−4m/s2
−8m/s2
−5m/s2
The correct Answer is:A
To find the component of the bullet's acceleration in the direction of its velocity, we can follow these steps:
Step 1: Understand the Problem
The bullet moves at an angle of 37∘ to the horizontal, and the acceleration due to gravity is 10m/s2 acting downwards. We need to find the component of this acceleration in the direction of the bullet's velocity.
Step 2: Draw a Diagram
- Draw a horizontal line to represent the ground.
- Draw a line at an angle of 37∘ above the horizontal to represent the direction of the bullet's velocity.
- Draw a vertical line downwards to represent the acceleration due to gravity.
Step 3: Identify Angles
- The angle between the acceleration vector (downward) and the velocity vector (at 37∘ to the horizontal) is 53∘ (since 90∘−37∘=53∘).
Step 4: Calculate the Component of Acceleration
To find the component of the acceleration vector in the direction of the velocity vector, we use the cosine of the angle between them. The formula for the component of acceleration a in the direction of velocity is:
acomponent=a⋅cos(θ)
where:
- a=10m/s2 (the magnitude of acceleration),
- θ=53∘ (the angle between the acceleration and the direction of velocity).
Step 5: Substitute Values
Now, substituting the values into the formula:
acomponent=10⋅cos(53∘)
Step 6: Calculate cos(53∘)
Using the cosine value:
cos(53∘)=35
Thus,
acomponent=10⋅35=6m/s2
Step 7: Determine the Direction
Since the acceleration is acting downward and the velocity is directed upwards at 37∘, the component of acceleration in the direction of the velocity is negative:
acomponent=−6m/s2
Final Answer
The component of the bullet's acceleration in the direction of its velocity is:
−6m/s2
The bullet moves at an angle of 37∘ to the horizontal, and the acceleration due to gravity is 10m/s2 acting downwards. We need to find the component of this acceleration in the direction of the bullet's velocity.
- Draw a horizontal line to represent the ground.
- Draw a line at an angle of 37∘ above the horizontal to represent the direction of the bullet's velocity.
- Draw a vertical line downwards to represent the acceleration due to gravity.
- The angle between the acceleration vector (downward) and the velocity vector (at 37∘ to the horizontal) is 53∘ (since 90∘−37∘=53∘).
To find the component of the acceleration vector in the direction of the velocity vector, we use the cosine of the angle between them. The formula for the component of acceleration a in the direction of velocity is:
acomponent=a⋅cos(θ)
where:
- a=10m/s2 (the magnitude of acceleration),
- θ=53∘ (the angle between the acceleration and the direction of velocity).
Now, substituting the values into the formula:
acomponent=10⋅cos(53∘)
Using the cosine value:
cos(53∘)=35
Thus,
acomponent=10⋅35=6m/s2
Since the acceleration is acting downward and the velocity is directed upwards at 37∘, the component of acceleration in the direction of the velocity is negative:
acomponent=−6m/s2
The component of the bullet's acceleration in the direction of its velocity is:
−6m/s2
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Multiple Correct Type Questions.
3 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) ComprehensionType Questions.
3 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
An aeroplane takes off at an angle of 60∘ to the horizontal.If the velocity of the plane is 200kmh−1,calculate its horizontal and vertical component of its velocity.
View SolutionIf acceleration of block B is 4m/s2 upward & that of C is 6m/s2 downward. Find acceleration of A :−
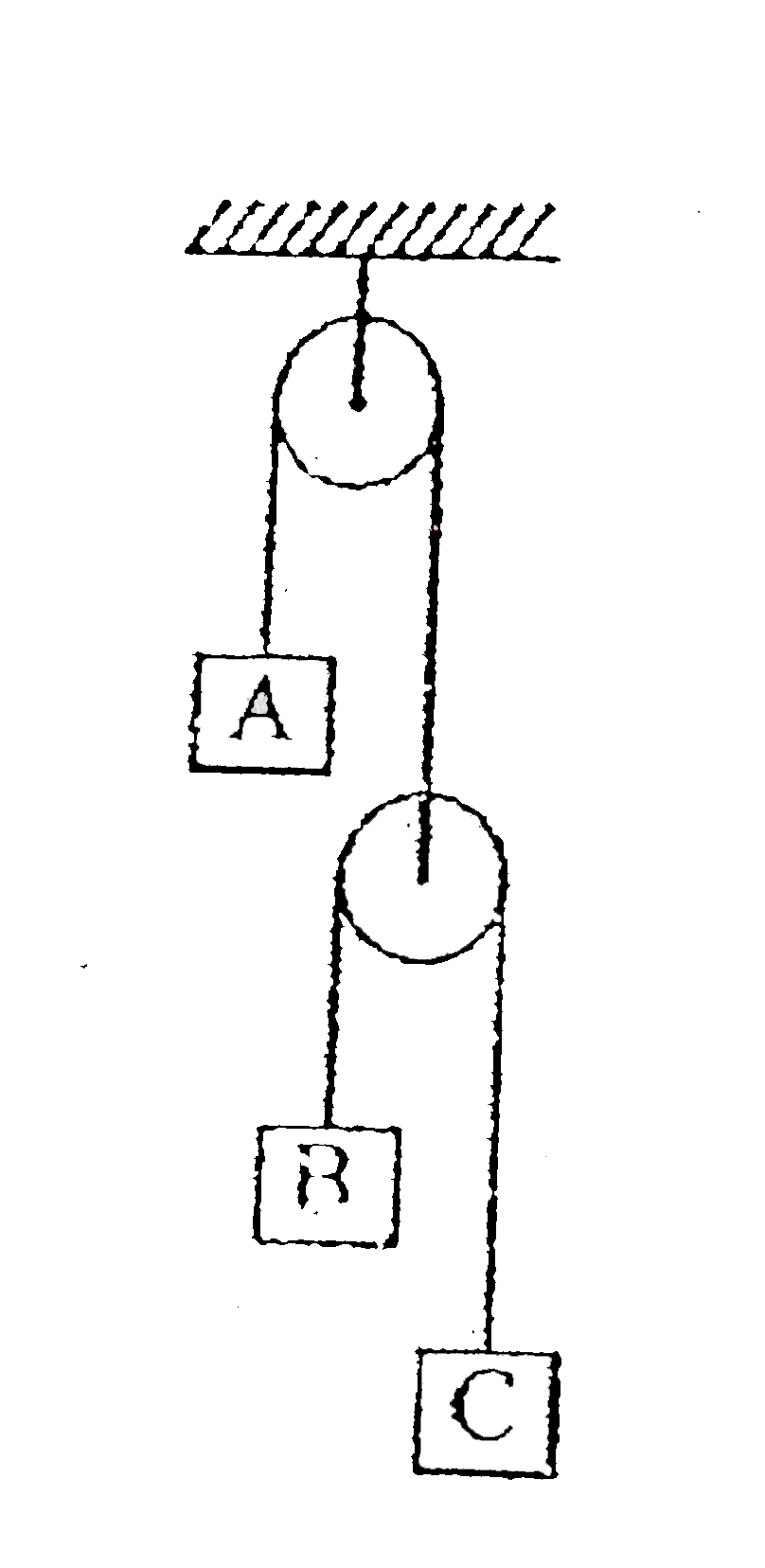
View SolutionFor any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
→a=10ˆi+15ˆj+20ˆk
Find the tangential acceleration of the particle at the given instant :-
View SolutionFor any particle moving with some velocity (→v) & acceleration (→a), tangential acceleration & normal acceleration are defined as follows.
Tangential acceleration - The component of acceleration in the direction of velocity.
Normal acceleration - The component of acceleration in the direction perpendicular to velocity.
If at a given instant, velocity & acceleration of a particle are given by .
→c=4ˆi+3ˆj
→a=10ˆi+15ˆj+20ˆk
Find the normal acceleration of the particles at the given instant :-
View SolutionA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
View SolutionA projectile is fired at an angle of 30∘ to the horizontal such that the vertical component of its initial velocity is 80m/s. Its time of fight is T. Its velocity at t=T/4 has a magnitude of nearly.
View SolutionA particle is moving with velocity v=100ms−1. If one of the rectangular components of a velocity is 50ms−1. Find the other component of velocity and its angle with the given component of velocity.
View SolutionA car accelerates at a rate of 5m s−2. Find the increase in its velocity in 2 s.
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
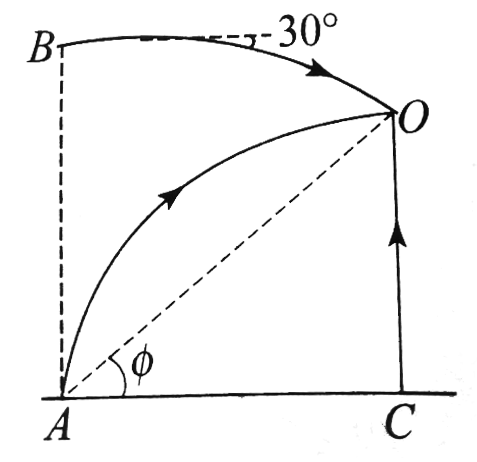
Find the velocity of bullet at A:
View SolutionAn object is projected from ground with speed 20 m/s at angle 30∘ with horizontal. Its centripetal acceleration one second after the projection is
[ Take g = 10 m/s2 ]
View Solution
