The kinetic energy of a particle of mass m moving with speed v is given by K=12mv2. If the kinetic energy of a particle moving along x-axis varies with x as K(x)=9−x2, then The region in which particle lies is :
x≥9
−3≤x≤3
0≤x≤9
−∞<x<∞
The correct Answer is:2
To solve the problem, we need to analyze the given kinetic energy function and determine the region in which the particle can move based on its kinetic energy being non-negative.
1. Understand the Kinetic Energy Function:
The kinetic energy K of a particle is given by the equation:
K=12mv2
We are also given that the kinetic energy varies with position x as:
K(x)=9−x2
2. Set Up the Condition for Kinetic Energy:
Since kinetic energy cannot be negative, we set up the inequality:
K(x)≥0
Substituting the expression for K(x):
9−x2≥0
3. Rearrange the Inequality:
Rearranging the inequality gives:
x2≤9
4. Solve for x:
Taking the square root of both sides, we find:
−3≤x≤3
This means that x can take any value between -3 and 3, inclusive.
5. Conclusion:
Therefore, the region in which the particle lies is:
x∈(−3,3)
Final Answer:
The particle lies in the region x∈(−3,3).
---
The kinetic energy K of a particle is given by the equation:
K=12mv2
We are also given that the kinetic energy varies with position x as:
K(x)=9−x2
Since kinetic energy cannot be negative, we set up the inequality:
K(x)≥0
Substituting the expression for K(x):
9−x2≥0
Rearranging the inequality gives:
x2≤9
Taking the square root of both sides, we find:
−3≤x≤3
This means that x can take any value between -3 and 3, inclusive.
Therefore, the region in which the particle lies is:
x∈(−3,3)
The particle lies in the region x∈(−3,3).
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-II AIPMT/NEET & AIIMS (2006- 2018)6videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
Similar Questions
Kinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionThe kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure
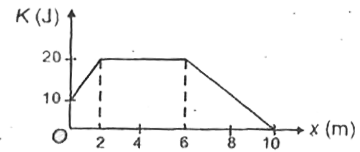
The magnitude of force acting on particle at x = 9 misView SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionThe potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View SolutionThe potential energy of a particle of mass m is given by U=12kx2 for x<0 and U = 0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
View SolutionA particle of mass m has half the kinetic energy of another particle of mass m2. If the speed of the heavier particle is increased by 2ms−1 its new kinetic energy becomes equal to t he original kinetic energy of the lighter particle. The ratio of the orighinal speeds of the lighter and heavier particle is
View Solution

