Find the values of the following :-
The correct Answer is:(a)
(b)
(c )
(d)
To solve the given question, we need to find the values of the trigonometric functions for the specified angles. Let's break it down step by step.
Step 1: Find sin(−30∘)
Using the property of sine, we know that:
sin(−θ)=−sin(θ)
Thus,
sin(−30∘)=−sin(30∘)
From trigonometric tables, we know:
sin(30∘)=12
Therefore,
sin(−30∘)=−12
Step 2: Find cos(−45∘)
Using the property of cosine, we know that:
cos(−θ)=cos(θ)
Thus,
cos(−45∘)=cos(45∘)
From trigonometric tables, we know:
cos(45∘)=1√2
Therefore,
cos(−45∘)=1√2
Step 3: Find sin(−60∘)
Using the property of sine again:
sin(−θ)=−sin(θ)
Thus,
sin(−60∘)=−sin(60∘)
From trigonometric tables, we know:
sin(60∘)=√32
Therefore,
sin(−60∘)=−√32
Step 4: Find tan(−45∘)
Using the property of tangent, we know that:
tan(−θ)=−tan(θ)
Thus,
tan(−45∘)=−tan(45∘)
From trigonometric tables, we know:
tan(45∘)=1
Therefore,
tan(−45∘)=−1
Final Answers
Now, we can summarize the answers:
- sin(−30∘)=−12
- cos(−45∘)=1√2
- sin(−60∘)=−√32
- tan(−45∘)=−1
Using the property of sine, we know that:
sin(−θ)=−sin(θ)
Thus,
sin(−30∘)=−sin(30∘)
From trigonometric tables, we know:
sin(30∘)=12
Therefore,
sin(−30∘)=−12
Using the property of cosine, we know that:
cos(−θ)=cos(θ)
Thus,
cos(−45∘)=cos(45∘)
From trigonometric tables, we know:
cos(45∘)=1√2
Therefore,
cos(−45∘)=1√2
Using the property of sine again:
sin(−θ)=−sin(θ)
Thus,
sin(−60∘)=−sin(60∘)
From trigonometric tables, we know:
sin(60∘)=√32
Therefore,
sin(−60∘)=−√32
Using the property of tangent, we know that:
tan(−θ)=−tan(θ)
Thus,
tan(−45∘)=−tan(45∘)
From trigonometric tables, we know:
tan(45∘)=1
Therefore,
tan(−45∘)=−1
Now, we can summarize the answers:
- sin(−30∘)=−12
- cos(−45∘)=1√2
- sin(−60∘)=−√32
- tan(−45∘)=−1
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Differentiation)
38 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - PHYSICS
13 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find the value of the following logcot30∘tan45∘
View SolutionFind the values of the following trignometric ratios:
(a) cos480∘
(b) sin1125∘
( c)tan(−480∘)
( d) cosec(−1200∘)
View SolutionABC is an isosceles right-angled triangle. Assuming AB = BC = x, find the value of each of the following trigonometric ratios :
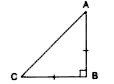
(i) sin45∘
(ii) cos45∘
(iii) tan45∘
View SolutionFind the value of sin30∘cos245∘−tan260∘+3cos90∘+sin0∘.
View SolutionFind the value of x in the following :
cos2x=cos60cos30 + sin60sin30
View SolutionFind the value of :
3sin230∘+2tan260∘−5cos245∘
View SolutionFind the value of :
3sin230∘+2tan260∘−5cos245∘
View SolutionFind the value of :
tan45∘cosec30∘+sec60∘cot45∘−5sin90∘2cos0∘
View SolutionFind the value of :
sin30∘−sin90∘+2cos0∘tan30∘×tan60∘
View Solutionusing trigonometric tables evaluate the following :
cot30∘sec30∘+cosec 30∘tan45∘−2cos0∘sin30∘+cos245∘
View Solution
