Calculate the value of following :-
cos75∘
The correct Answer is:(a) cos75∘=√3−12√2 (b) sin 15∘=√3−12√2
(c ) sin75∘=√3+12√2
(d)cos105∘=−(√3−12√2) or 1−√32√2
To calculate the value of cos75∘, we can use the cosine addition formula. Here’s how to do it step-by-step:
Step 1: Rewrite cos75∘
We can express 75∘ as the sum of two angles:
75∘=45∘+30∘
Thus, we can write:
cos75∘=cos(45∘+30∘)
Step 2: Apply the Cosine Addition Formula
The cosine addition formula states:
cos(a+b)=cosacosb−sinasinb
Using this formula, we can write:
cos75∘=cos45∘cos30∘−sin45∘sin30∘
Step 3: Substitute Known Values
We know the following trigonometric values:
- cos45∘=1√2
- cos30∘=√32
- sin45∘=1√2
- sin30∘=12
Substituting these values into the equation gives:
cos75∘=(1√2)(√32)−(1√2)(12)
Step 4: Simplify the Expression
Now, we simplify the expression:
cos75∘=√32√2−12√2
Combining the two fractions:
cos75∘=√3−12√2
Final Result
Thus, the value of cos75∘ is:
cos75∘=√3−12√2
---
We can express 75∘ as the sum of two angles:
75∘=45∘+30∘
Thus, we can write:
cos75∘=cos(45∘+30∘)
The cosine addition formula states:
cos(a+b)=cosacosb−sinasinb
Using this formula, we can write:
cos75∘=cos45∘cos30∘−sin45∘sin30∘
We know the following trigonometric values:
- cos45∘=1√2
- cos30∘=√32
- sin45∘=1√2
- sin30∘=12
cos75∘=(1√2)(√32)−(1√2)(12)
Now, we simplify the expression:
cos75∘=√32√2−12√2
Combining the two fractions:
cos75∘=√3−12√2
Thus, the value of cos75∘ is:
cos75∘=√3−12√2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Differentiation)38videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Integration)12videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - PHYSICS13videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
Calculate the value of x in the following figure :
 View Solution
View SolutionCalculate the value of x in the following figure :
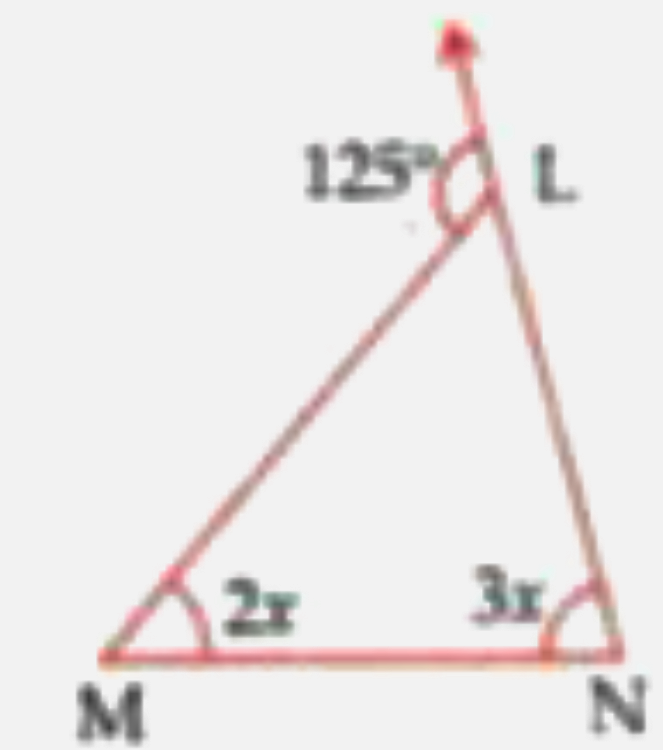 View Solution
View SolutionCalculate the value of x in the following figure :
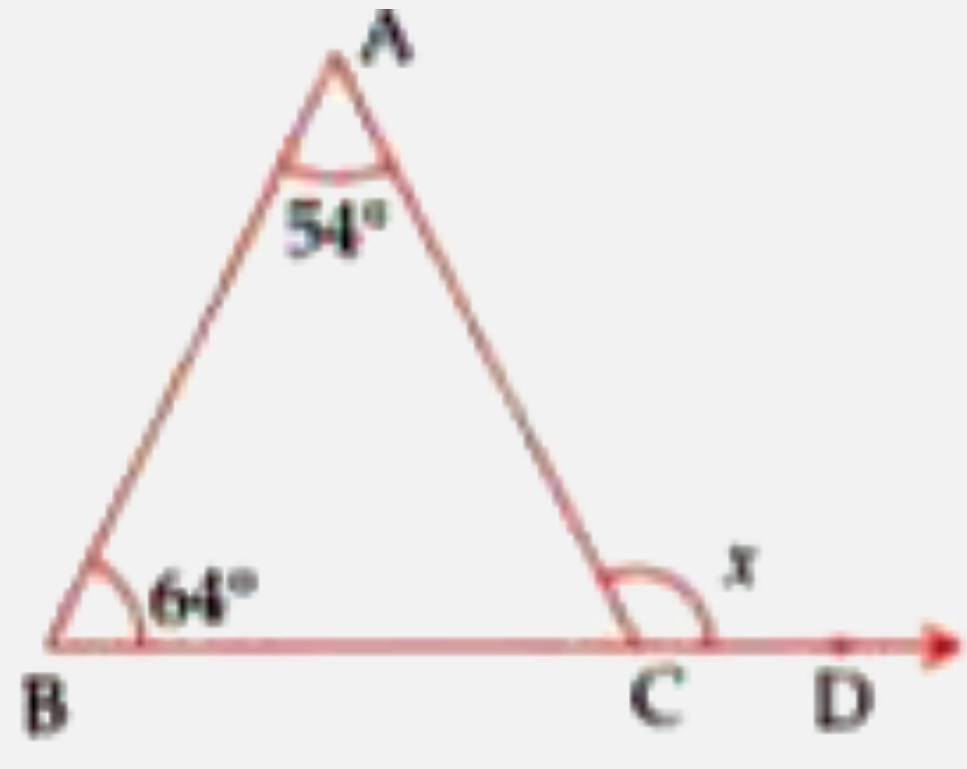 View Solution
View SolutionCalculate the pH value of the following
0.001 M HCIView SolutionThe value of tan75
View SolutionCalculate the pH value of the following
0.01 M NaOH.View SolutionCalculate the value of A, if :
cos3A.(2sin2A−1)=0View SolutionCalculate the value of A, if :
cos3A.(2sin2A−1)=0View SolutionCalculate the value of x in each of the following sketches:
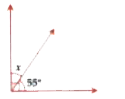 View Solution
View SolutionCalculate the value of x in each of the following sketches:
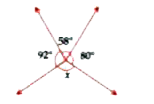 View Solution
View Solution

