Statement 1 : For very small angle θ, we may use approximation sinθ≈θ≈tanθ.
and
Statement 2 : For very small angle θ, the hypotenuse and the base become approximately of the same length.
(1) Statement-1 is True, Statement-2 is True,
Statement-2 is a correct explanation for
Statement-1.
(2)Statement-1 is True, Statement-2 is True,
Statemen-2 is not a correct explanation for
Statement-1
(3)Statement-1 is True, Statement-2 is False.
(4)Statemen-1 is False, Statement-2 is True.
The correct Answer is:A
To analyze the statements provided in the question, we will break down each statement and understand their implications step by step.
Step 1: Understanding Statement 1
Statement 1: For very small angle θ, we may use the approximation sinθ≈θ≈tanθ.
- For small angles (in radians), the values of sinθ and tanθ can be approximated by the angle itself. This is derived from the Taylor series expansions of sine and tangent functions.
- As θ approaches 0, both sinθ and tanθ approach θ.
Step 2: Understanding Statement 2
Statement 2: For very small angle θ, the hypotenuse and the base become approximately of the same length.
- In a right triangle, if we denote the opposite side as a, the base as b, and the hypotenuse as c, we can analyze the relationships.
- As θ becomes very small, the height a (opposite side) becomes very small compared to the base b (adjacent side) and the hypotenuse c.
- In this case, the base b and the hypotenuse c can be considered approximately equal because the angle θ is small, leading to a very flat triangle.
Step 3: Conclusion
- Since both statements are true, we can conclude that Statement 1 is correct, and Statement 2 provides a correct explanation for Statement 1.
Final Answer
Both statements are true, and Statement 2 is a correct explanation of Statement 1.
---
Statement 1: For very small angle θ, we may use the approximation sinθ≈θ≈tanθ.
- As θ approaches 0, both sinθ and tanθ approach θ.
Statement 2: For very small angle θ, the hypotenuse and the base become approximately of the same length.
- As θ becomes very small, the height a (opposite side) becomes very small compared to the base b (adjacent side) and the hypotenuse c.
- In this case, the base b and the hypotenuse c can be considered approximately equal because the angle θ is small, leading to a very flat triangle.
- Since both statements are true, we can conclude that Statement 1 is correct, and Statement 2 provides a correct explanation for Statement 1.
Both statements are true, and Statement 2 is a correct explanation of Statement 1.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Differentiation)
38 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - PHYSICS
13 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Assertion:− For a very small ∠θ ,sinθ≈θ.
Reason :−At very small angle, arc, subtends a right angle at the centre of arc.
View SolutionStatement 1 : (acos2θ,2acosθ) is the parametric point of parabola y2=4ax. Statement 2: For all value of θ,−1≤cosθ≤1
View SolutionStatement-1: f(θ)=sin2θ+cos2θ
then f(θ)=1 for every real values of θ.
Statement:2: g(θ)=sec2θ−tan2θ.
then g(θ)=1 for every real value of θ.
Statement-3: f(θ)=g(θ) for every real value of θ.
View SolutionIf the angle between the vectors a and b be θanda⋅b=cosθ then the true statement is
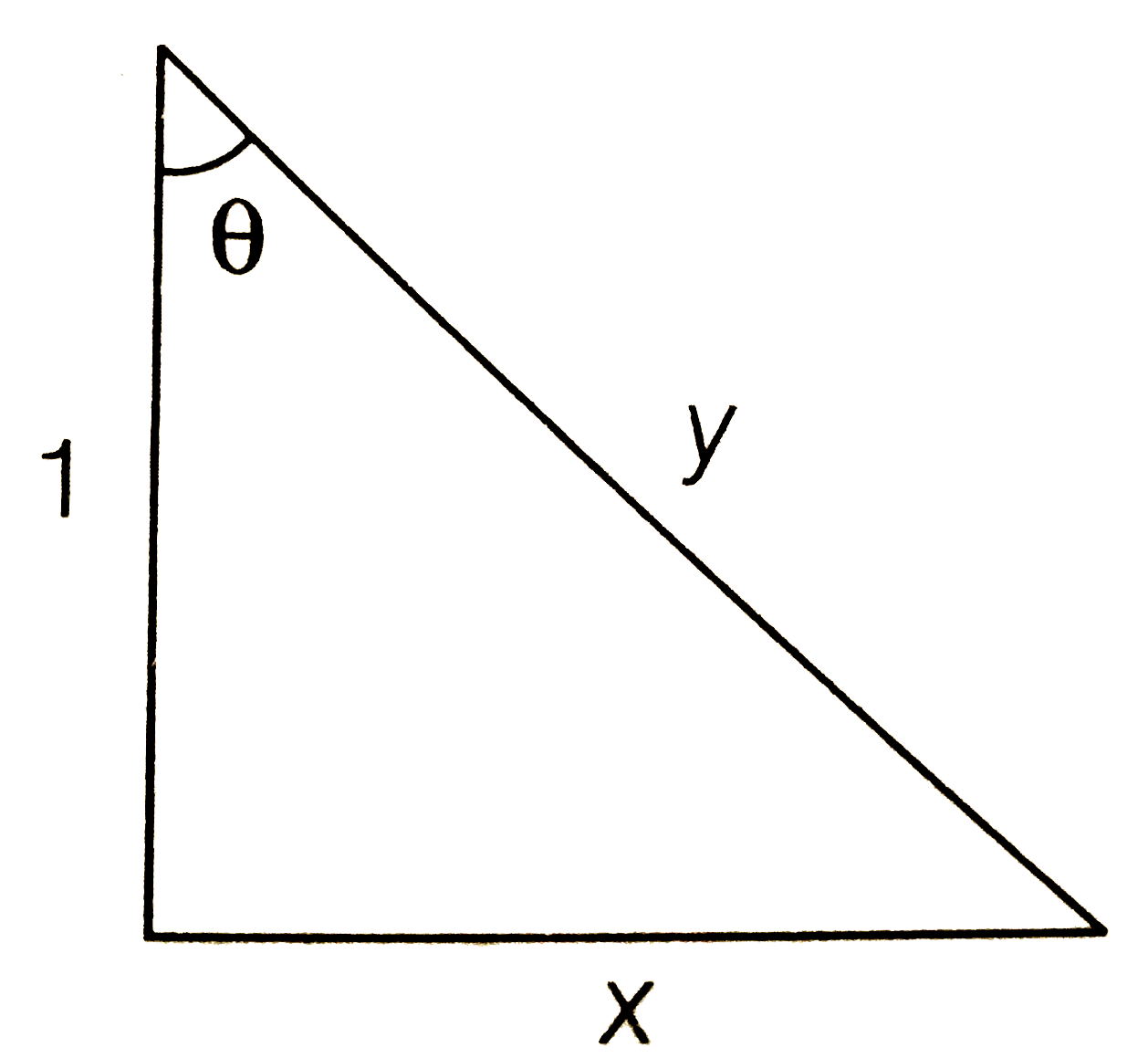
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as

View SolutionStatement I The maximum value of sinθ+cosθ is 2.
Statement II The maximum value of sinθ is 1 and that of cosθ is also 1.
View SolutionA vector →a is turned without a change in its length through a small angle dθ. Find the value of |Δ→a|
View SolutionStatement I If 2cosθ+sinθ=1(θ≠π2) then the value of 7cosθ+6sinθ is 2.
Statement II If cos2θ−sinθ=12,0<θ<π2, then sinθ+cos6θ=0.
View SolutionProve that :sinθ+sin2θ1+cosθ+cos2θ=tanθ
View SolutionThe range of a projectile when launched at angle θ is same as when launched at angle 2θ. What is the value of θ ?
View Solution
