In the figure chords AE and BC intersect each other at point D
(i) If ∠CDE=90∘
AB=5cm
BD=4cm and CD=9 cm
find DE
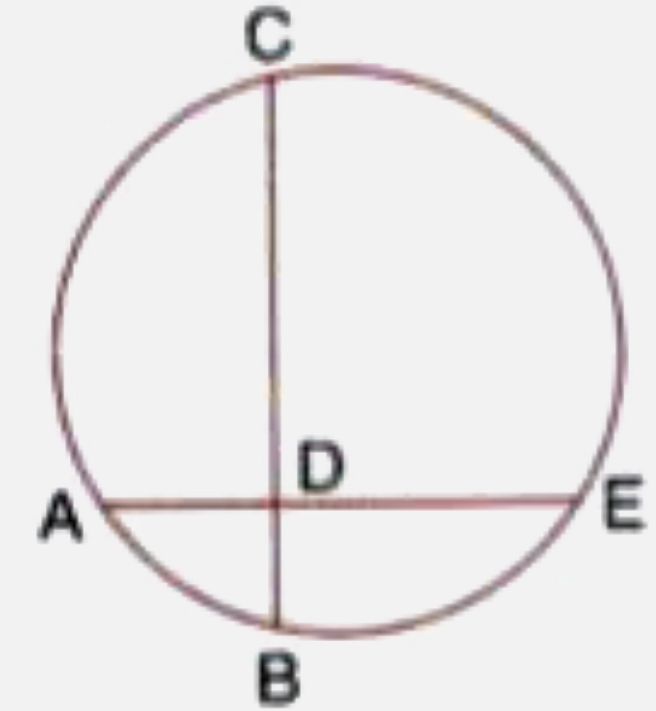
(ii) If AD=BD, show that AE=BC
The correct Answer is:(i) DE=12cm
Step by step video & image solution for In the figure chords AE and BC intersect each other at point D (i) If /_CDE=90^(@) AB=5cm BD=4cm and CD=9 cm find DE (ii) If AD=BD, show that AE=BC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (C)
Explore 42 Videos
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18(A)
Explore 24 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)Book:ICSEChapter:SPECIMEN QUESTION PAPER (MATHEMATICS)Exercise:Section C
Explore 12 Videos
- TRIGONOMETRICAL IDENTITIESBook:ICSEChapter:TRIGONOMETRICAL IDENTITIESExercise:QUESTIONS
Explore 22 Videos
Similar Questions
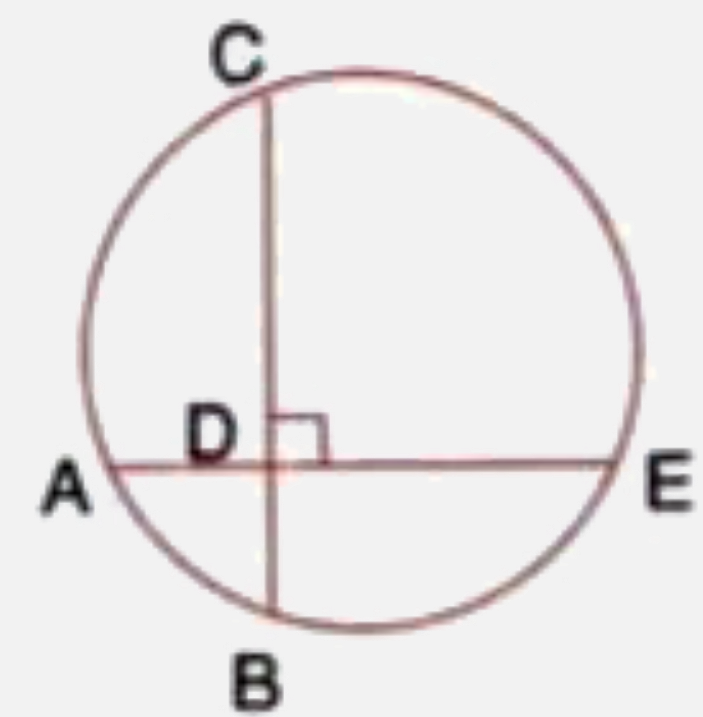
In the given figure, AE and BC intersect each other at point D.
If ∠CDE=90∘,AB=5cm,BD=4 and CD=9 find AE
View SolutionIn the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
View SolutionIn the given figure, AB and DE are perpendicular to BC.

(iI) If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
View Solutionin a figure DE||BC AD=3cm, BD =4cm and BC=14cm, then DE equals
View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.

If BD = 18 cm and CD = 8 cm, find AD.
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
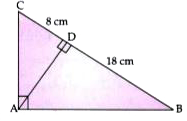
If BD = 18 cm, CD = 8 cm find AD.
View SolutionIn given figure, check whether AD is the bisector of ∠ A of △ ABC in each of the following: (i) AB = 5 cm, AC = 10 cm, BD = 1.5 cm and CD = 3.5 cm (ii) AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm (iii) AB = 8 cm, AC = 24 cm, BD = 6 cm and BC = 24 cm (iv) AB = 6 cm, AC = 8 cm, BD = 1.5 cm and CD = 2 cm (v) AB = 5 cm, AC = 12 cm, BD = 2.5 cm and BC = 9 cm
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

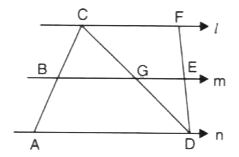
View SolutionIn the following figure, straight lines . m and n are parallel to each other and is the mid-point of CD. Find
(1) BG, if AD = 12 cm
(ii) CF, if GE = 4.6 cm
(iii) AB, if BC = 4.8 cm
(iv) ED, if FD = 8.8 cm
View Solutionin the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.

View Solution
