A particle with a mass of a velocity of is having in -direction at . Forces and , act on the particle whose magnitudes are changing with time according to the variation shown in Fig. The magnitude of the velocity of the particle at (neglect gravity effect) is found to be Find the value of
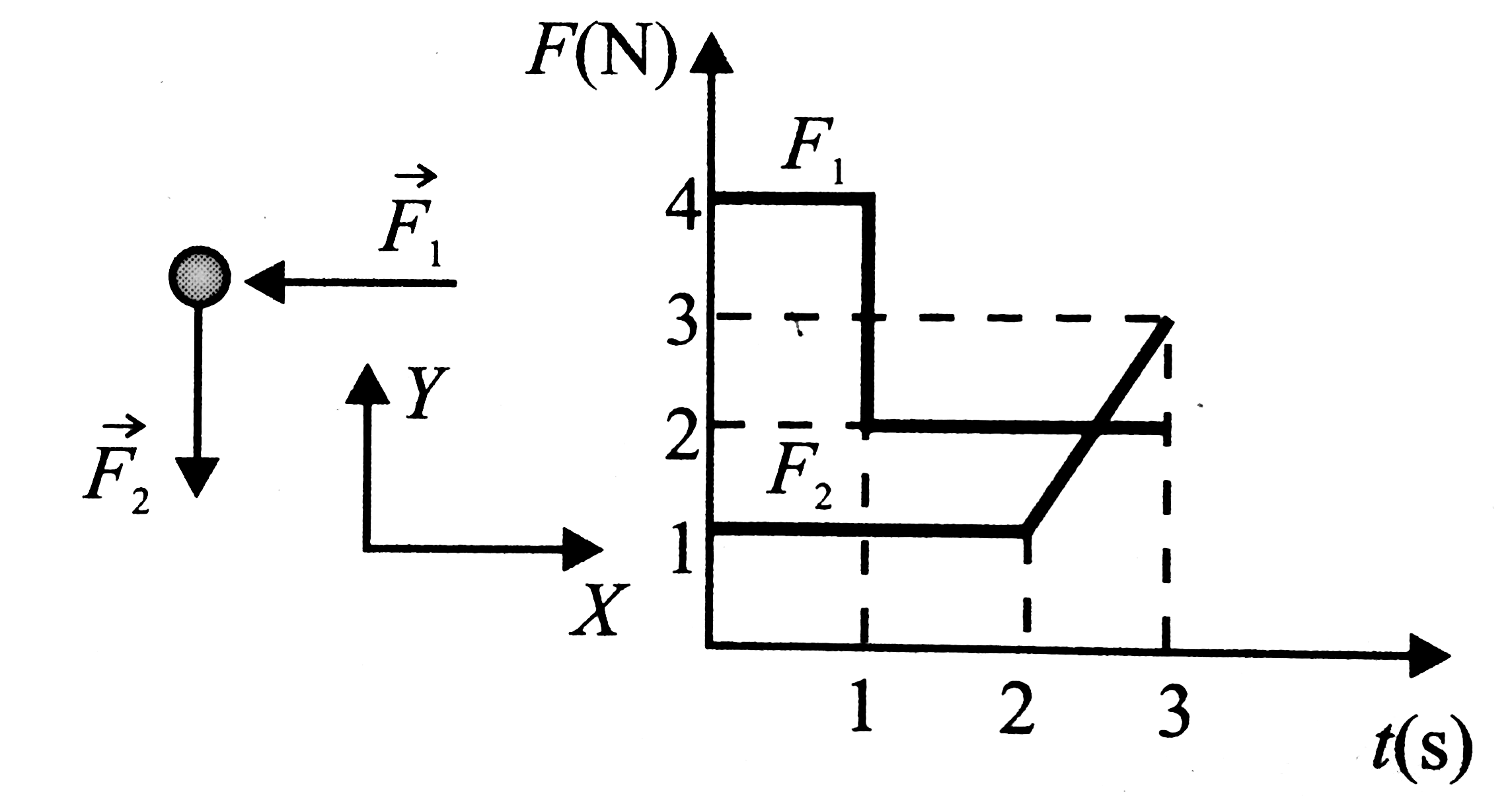
The correct Answer is:2
Initial velocity of the particle is
From impulse momentum theorem,
(where is the required velocity)
or
or
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A particle executes SHM according to equation x=10(cm)cos[2πt+π2], where t is in seconds. The magnitude of the velocity of the particle at t=16s will be :-
View SolutionA particle of mass 2kg is initially at rest. A force starts acting on it in one direction whose magnitude changes with time. The force time graph is shown in figure. Find the velocity of the particle at the end of 10s.
 View Solution
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
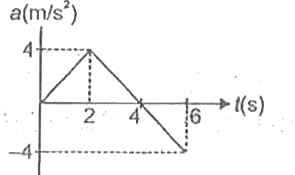 View Solution
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
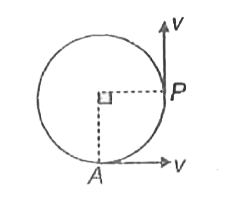 View Solution
View SolutionTwo particles are shown in figure. At t=0 a constant force F=6N starts acting on 3kg. Find the velocity of circle of mass of these particle at t=5s.
 .View Solution
.View SolutionA particle of mass 1 g moves on a straight line. The variation of its velocity with time is shown in fig. Find the force acting on the particle att = 1 s,4s and 7 s.
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be
 View Solution
View SolutionA particle of mass m is acted on by two forces of equal magnitude F maintaining their orientation relative to the velocity v as shown in Fig. The momentum of the particle
 View Solution
View SolutionThe force(F) acting on a particle of mass m changing with time(t) is as shown in (F−t) graph. The change in linear momentum from t=0 to t=6 s (in kN s) is
 View Solution
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View Solution

