Rank the launch angles for the five path in the figure below with respect to time of flight, from the shortest time of fight the longest :-
15∘,30∘,45∘,60∘,75∘
75∘,60∘,45∘,30∘,15∘
15∘,75∘,30∘,60∘,45∘
30∘,60∘,15∘,45∘,75∘
The correct Answer is:A
To solve the problem of ranking the launch angles with respect to time of flight from shortest to longest, we can follow these steps:
Step 1: Understand the formula for time of flight
The time of flight T for a projectile launched at an angle θ is given by the formula:
T=2asinθg
where:
- a is the initial velocity,
- g is the acceleration due to gravity,
- θ is the launch angle.
Step 2: Analyze the sine function
The sine function sinθ varies with the angle θ:
- sin0∘=0
- sin15∘
- sin30∘=12
- sin45∘=√22
- sin60∘=√32
- sin75∘
As the angle increases from 0∘ to 90∘, the value of sinθ increases. Therefore, the time of flight T will also increase with increasing θ.
Step 3: List the angles and their sine values
- 15∘ → sin15∘
- 30∘ → sin30∘=0.5
- 45∘ → sin45∘=√22≈0.707
- 60∘ → sin60∘=√32≈0.866
- 75∘ → sin75∘
Step 4: Rank the angles based on sine values
Since T is directly proportional to sinθ, we can rank the angles based on the sine values:
- The smallest sine value corresponds to the smallest angle, which will have the shortest time of flight.
- The largest sine value corresponds to the largest angle, which will have the longest time of flight.
Step 5: Determine the order
From the sine values, we can determine the order:
1. 15∘ (smallest)
2. 30∘
3. 45∘
4. 60∘
5. 75∘ (largest)
Final Ranking
Thus, the ranking of the launch angles from the shortest time of flight to the longest is:
1. 15∘
2. 30∘
3. 45∘
4. 60∘
5. 75∘
Conclusion
The correct answer is that the launch angles ranked from shortest to longest time of flight are:
- 15∘,30∘,45∘,60∘,75∘
The time of flight T for a projectile launched at an angle θ is given by the formula:
T=2asinθg
where:
- a is the initial velocity,
- g is the acceleration due to gravity,
- θ is the launch angle.
The sine function sinθ varies with the angle θ:
- sin0∘=0
- sin15∘
- sin30∘=12
- sin45∘=√22
- sin60∘=√32
- sin75∘
- 15∘ → sin15∘
- 30∘ → sin30∘=0.5
- 45∘ → sin45∘=√22≈0.707
- 60∘ → sin60∘=√32≈0.866
- 75∘ → sin75∘
Since T is directly proportional to sinθ, we can rank the angles based on the sine values:
- The smallest sine value corresponds to the smallest angle, which will have the shortest time of flight.
- The largest sine value corresponds to the largest angle, which will have the longest time of flight.
From the sine values, we can determine the order:
1. 15∘ (smallest)
2. 30∘
3. 45∘
4. 60∘
5. 75∘ (largest)
Thus, the ranking of the launch angles from the shortest time of flight to the longest is:
1. 15∘
2. 30∘
3. 45∘
4. 60∘
5. 75∘
The correct answer is that the launch angles ranked from shortest to longest time of flight are:
- 15∘,30∘,45∘,60∘,75∘
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (NEWTONS LAWS OF MOTION)46videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)14videos
RACE
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)30videos
RACE
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
For the given circuit shown in figure below, time constant is
 View Solution
View SolutionIn the figure shown, find.
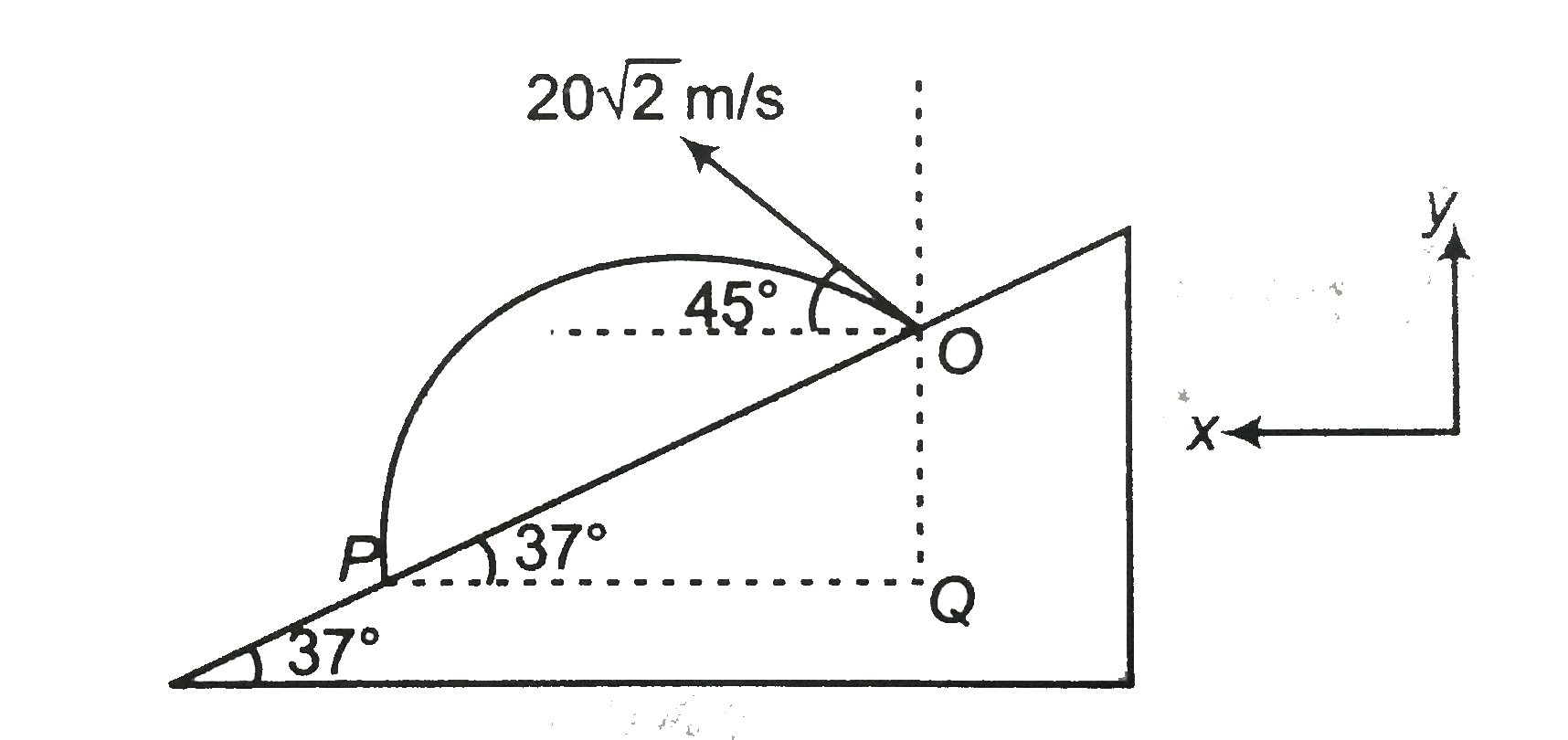
(a) time of flight of the projectile along the inclined plane.
(b) range OP.View SolutionIn the figure shown, find
 .
.
(a) the time of flight of the projectile over the inciled plane.
(b) range OP.View SolutionIn the figure shown, find.
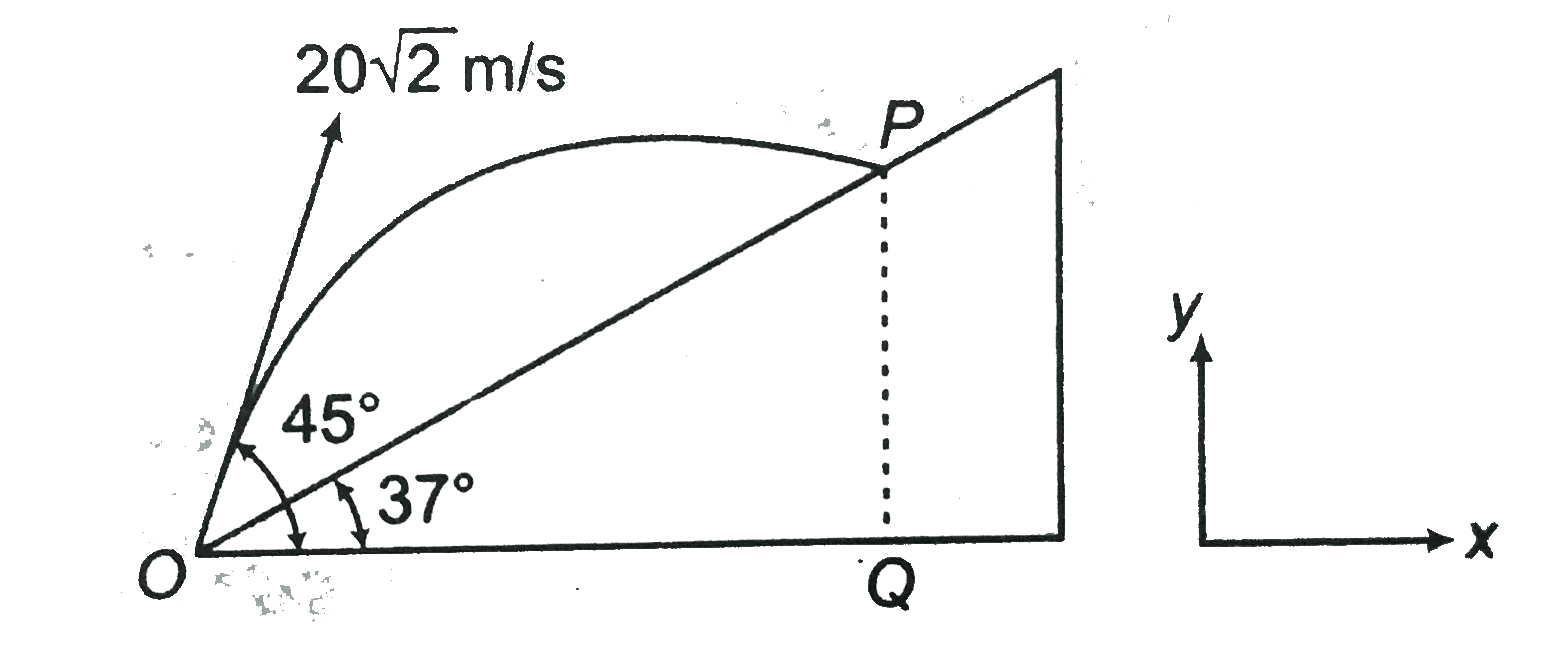
(a) time of flight of the projectile along the inclined plane.
(b) range OP.View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
 View Solution
View SolutionIn the circuit shown in figure switch S is closed at time t=0

Current I from the battery at time t is given byView SolutionRank the value of ∮→B→dl for the closed paths shown in figure from the smallest to largest.
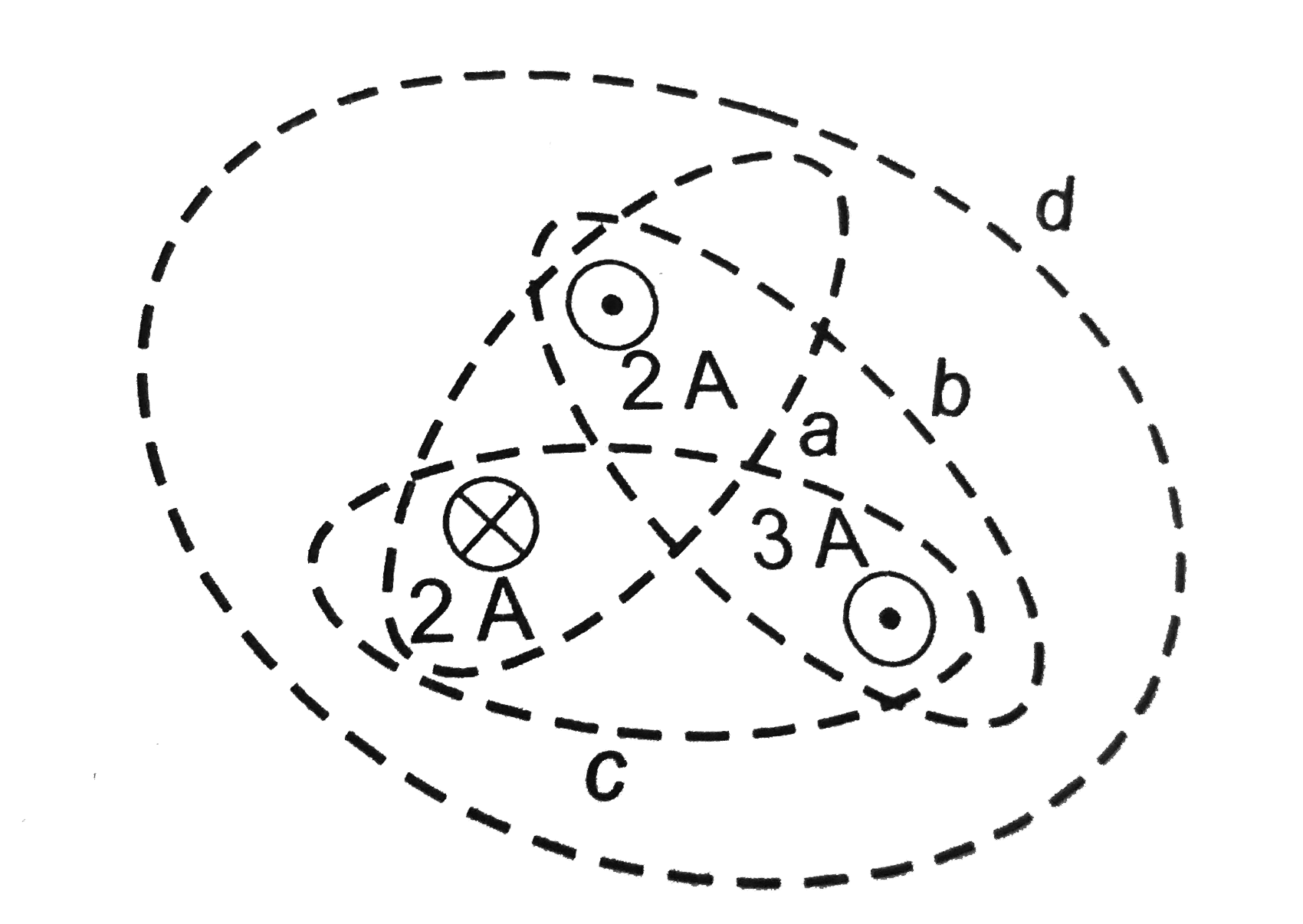 View Solution
View SolutionRank the value of ∮→B→dl for the closed paths shown in figure from the smallest to largest.
 View Solution
View SolutionA projectile can have same range R for two angles of projection. It t1andt2 are the times of flight in the two cases, then what is the product of two times of flight ?
View SolutionTo cross the river in shortest distance, a swimmer should swimming an angle θ with the upsteram. What is the ratio of the time taken to swim across in the shortest time to that in swimming across over shortest distance. [Asume that the speed of swimmer in still water is greater than the speed of river flow]
View Solution

