The diameter of the top of a firebrigade pump is 5 cm. Water is thrown by this pump at a horizontal speed of 18 m/s on a wall. If water rebounds back from the wall, then the force exerted by water on wall will be :-
2.35×105 dyne
5.76×106 dyne
6.36×107 dyne
12.72×107 dyne
The correct Answer is:D
To solve the problem of finding the force exerted by water on the wall when it rebounds, we can follow these steps:
Step 1: Calculate the area of the fire brigade pump
The diameter of the pump is given as 5 cm, so the radius r is:
r=5 cm2=2.5 cm=0.025 m
The area A of the top of the pump can be calculated using the formula for the area of a circle:
A=πr2=π(0.025)2=π(0.000625)≈0.0019635 m2
Step 2: Calculate the volume flow rate
The volume flow rate Q can be calculated using the formula:
Q=A⋅v
where v is the velocity of the water, given as 18 m/s. Thus,
Q=0.0019635 m2⋅18 m/s≈0.0353 m3/s
Step 3: Calculate the mass flow rate
The mass flow rate ˙m can be calculated using the density of water ρ (approximately 1000 kg/m³):
˙m=ρ⋅Q=1000 kg/m3⋅0.0353 m3/s≈35.3 kg/s
Step 4: Calculate the change in momentum
When the water hits the wall, it has an initial momentum pi=˙m⋅v and after rebounding, it has a final momentum pf=−˙m⋅v. Therefore, the change in momentum Δp is:
Δp=pf−pi=−˙m⋅v−˙m⋅v=−2˙m⋅v
Substituting the values:
Δp=−2⋅35.3 kg/s⋅18 m/s≈−1272 kg m/s
Step 5: Calculate the force exerted on the wall
The force F exerted by the water on the wall is given by the rate of change of momentum:
F=ΔpΔt=Δp (since we are considering per second)
Thus,
F=1272 N
Final Result
The force exerted by the water on the wall is approximately:
F≈1272 N
The diameter of the pump is given as 5 cm, so the radius r is:
r=5 cm2=2.5 cm=0.025 m
The area A of the top of the pump can be calculated using the formula for the area of a circle:
A=πr2=π(0.025)2=π(0.000625)≈0.0019635 m2
The volume flow rate Q can be calculated using the formula:
Q=A⋅v
where v is the velocity of the water, given as 18 m/s. Thus,
Q=0.0019635 m2⋅18 m/s≈0.0353 m3/s
The mass flow rate ˙m can be calculated using the density of water ρ (approximately 1000 kg/m³):
˙m=ρ⋅Q=1000 kg/m3⋅0.0353 m3/s≈35.3 kg/s
When the water hits the wall, it has an initial momentum pi=˙m⋅v and after rebounding, it has a final momentum pf=−˙m⋅v. Therefore, the change in momentum Δp is:
Δp=pf−pi=−˙m⋅v−˙m⋅v=−2˙m⋅v
Substituting the values:
Δp=−2⋅35.3 kg/s⋅18 m/s≈−1272 kg m/s
The force F exerted by the water on the wall is given by the rate of change of momentum:
F=ΔpΔt=Δp (since we are considering per second)
Thus,
F=1272 N
The force exerted by the water on the wall is approximately:
F≈1272 N
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
n bullet strikes per second elastically on wall and rebound then what will be the force exerted on the wall by bullets if mass of each bullet is m:-
View SolutionA horizontal jet of water coming out of a pipe of area of cross - section 20 cm2 hits a vertical wall with a velocity of 10 ms−1 and rebounds with the same speed. The force exerted by water on the wall is,
View SolutionThe height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is

View SolutionA ball hits a vertical wall horizontal at 10 m/s bounces back at 10 m/s
View SolutionWater from a hosepipe of radius 5 cm strikes a wall at a speed of 5ms−1 normally and stops. The force exerted on the wall in newton is
View SolutionA body of mass 2kg collides with a wall with speed 100 m/s and rebounds with same speed. If the time of contact was 1/50 second, the force exerted on the wall is
View SolutionA stream of water of density ρ, cross sectional area A, and speed u strikes a wall that is perpendicular to the direction of the stream, as shown in the figure below. The water then flows sideways across the wall. The force exerted by the stream on the wall is
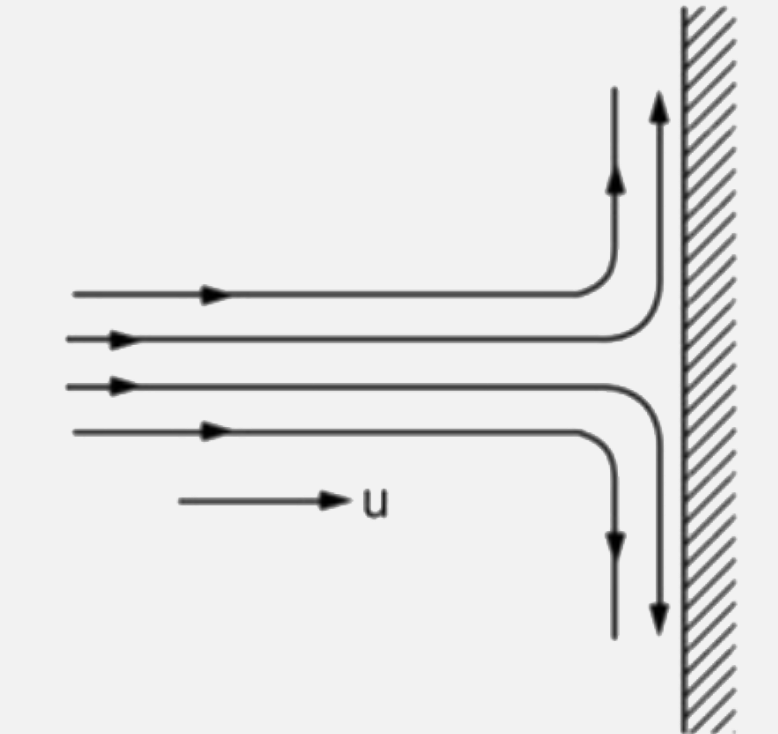
View SolutionA water pipe has an internal diameter of 10 cm. Water flows through it at the rate of 20 m/sec. The water jet strikes normally on a wall and falls dead. Find the force on the wall.
View SolutionA stream of a liquid of density p flowin horizontally with speed v rushes out of a tube of radius r and hits a verticla wall nearly normally. Assumi g that the liquid does not rebound from the wall, the force exerted o the wall by the impact of the liquid is given by
View SolutionA ball is thrown from the ground to clear a wall 3 m high at a distance of 6 m and falls 18 m away from the wall. Find the angle of projection of ball.
View Solution
