Fot the given momentume-time (P-t) graphs find the ratio of force on particles A & B.
The correct Answer is:FAFB=tan30∘tan45∘=1√3
To solve the problem of finding the ratio of forces on particles A and B from the given momentum-time (P-t) graphs, we can follow these steps:
Step 1: Understand the relationship between force and momentum
The force acting on an object is defined as the rate of change of momentum. Mathematically, this is expressed as:
F=dpdt
where F is the force, p is the momentum, and t is time.
Step 2: Identify the slopes of the P-t graphs
The slope of the momentum-time graph (P-t graph) represents the force. Therefore, we need to determine the slopes of the lines representing forces A and B on the graph.
Step 3: Determine the angles of the lines
From the problem, we know that:
- The angle of line A (force A) is 30∘.
- The angle of line B (force B) is 45∘.
Step 4: Calculate the slopes using the tangent of the angles
The slope of a line in a graph can be calculated using the tangent of the angle it makes with the horizontal axis:
slope=tan(θ)
Thus, we can write:
- Slope of line A:
slopeA=tan(30∘)
- Slope of line B:
slopeB=tan(45∘)
Step 5: Find the values of the tangents
Using known values:
- tan(30∘)=1√3
- tan(45∘)=1
Step 6: Set up the ratio of forces
Since the force is proportional to the slope, we can express the ratio of forces FA and FB as:
FAFB=tan(30∘)tan(45∘)
Step 7: Substitute the values of the tangents
Substituting the values we found:
FAFB=1√31=1√3
Step 8: Express the ratio in a simpler form
This can also be expressed as:
FA:FB=1:√3
Final Answer
Thus, the ratio of the forces on particles A and B is:
FA:FB=1:√3
---
The force acting on an object is defined as the rate of change of momentum. Mathematically, this is expressed as:
F=dpdt
where F is the force, p is the momentum, and t is time.
The slope of the momentum-time graph (P-t graph) represents the force. Therefore, we need to determine the slopes of the lines representing forces A and B on the graph.
From the problem, we know that:
- The angle of line A (force A) is 30∘.
- The angle of line B (force B) is 45∘.
The slope of a line in a graph can be calculated using the tangent of the angle it makes with the horizontal axis:
slope=tan(θ)
Thus, we can write:
- Slope of line A:
slopeA=tan(30∘)
- Slope of line B:
slopeB=tan(45∘)
Using known values:
- tan(30∘)=1√3
- tan(45∘)=1
Since the force is proportional to the slope, we can express the ratio of forces FA and FB as:
FAFB=tan(30∘)tan(45∘)
Substituting the values we found:
FAFB=1√31=1√3
This can also be expressed as:
FA:FB=1:√3
Thus, the ratio of the forces on particles A and B is:
FA:FB=1:√3
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
From the given graph , find time period and frequency for A and B.
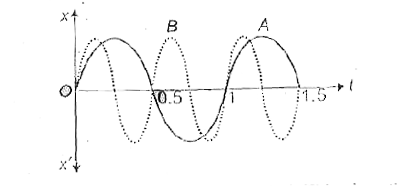
View SolutionA particle of mass 2kg is initially at rest. A force starts acting on it in one direction whose magnitude changes with time. The force time graph is shown in figure. Find the velocity of the particle at the end of 10s.

View SolutionThe velocity-time graph is given below
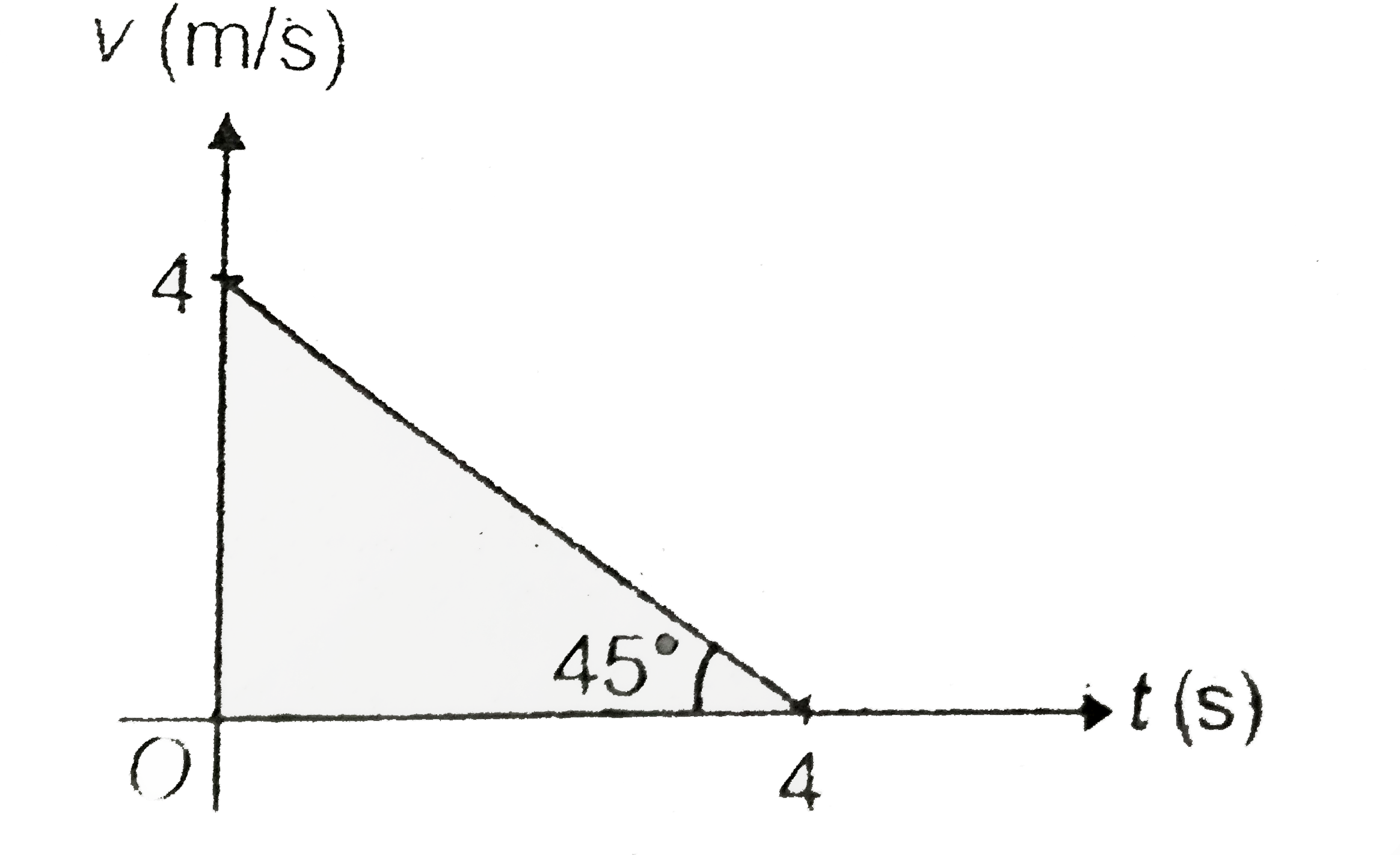
Draw the acceleration-time graph and position-time graph, given that at t = 0, particle is at origin.
View SolutionFigure a represents the speed-time graph for a particle .Find the distance covered by the particle betweent=10 min and t= 30 min .

View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t=t1andt=t2.

View SolutionFrom the given graph , find time period and frequency for A and B.
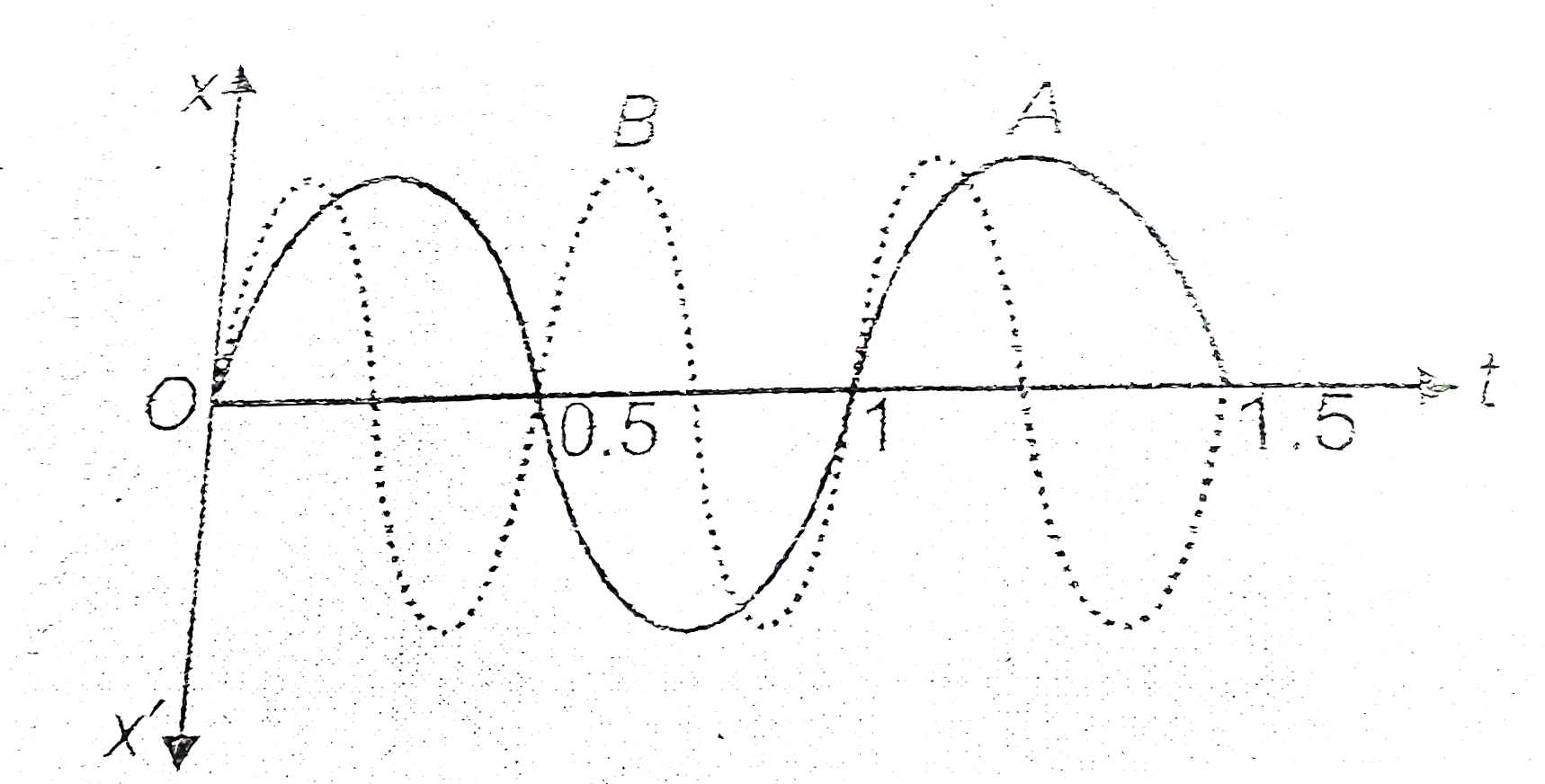
Hint : Find the time after which the motion is repeated . This gives time period T. Frequency v=1T0
View SolutionThe velocity →v of a particle of mass 'm' acted upon by a constant force is given by →v(t)=A[cos(kt)¯i−sin(kt)¯j] . Then the angle between the force and the momentum of the particle is (Here A and k are constants)
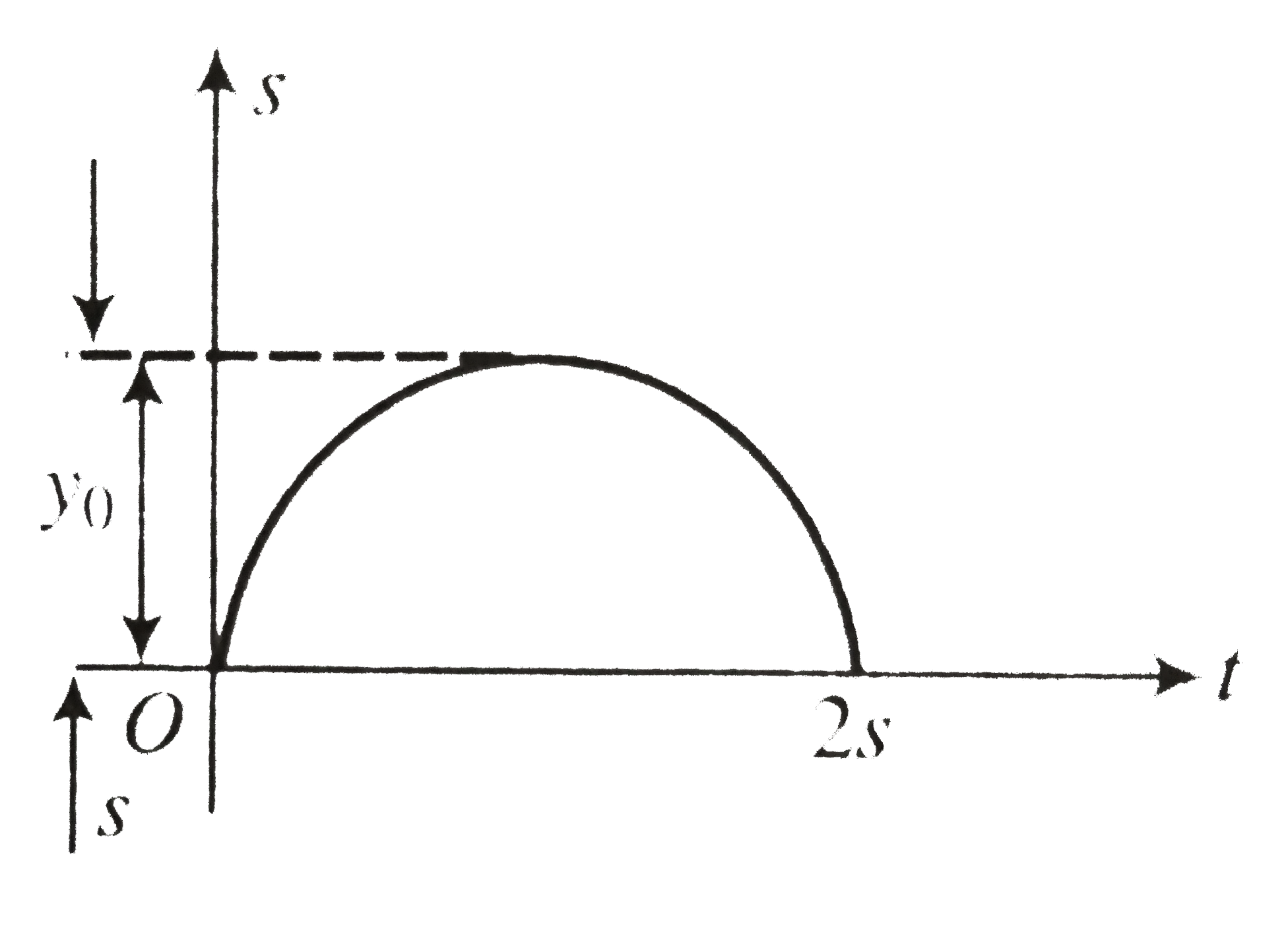
View SolutionA particle moves rectilinearly possessing a parabolic s-t graph. Find the average velocity of the particle over a time interval from t=12s→t=1.5s.
View SolutionA particle of mass is moving in a straight line with momentum p. Starting at time t= 0, a force F= kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here k is constant . The value of T is :
View SolutionThe velocity-time (v-t) graph for a particle in a straight line motion is given below The corresponding accelaration-time (a-t) graph will
View Solution
