The exhaust velocity of gases with respect to a small rocket of mass 25 kg. is 28×102m/s. At what rate the fuel must burn so that it may rise up with an acceleration of 9.8m/s2?
175 Kg
1.75 Kg/s
0.175 Kg/s
Zero
The correct Answer is:C
To solve the problem, we need to determine the rate at which the fuel must burn for the rocket to achieve the desired upward acceleration. We'll use the principles of thrust and Newton's second law of motion.
1. Identify the Given Data:
- Mass of the rocket (m) = 25 kg
- Exhaust velocity of gases (v) = 28×102 m/s = 2800 m/s
- Required acceleration (a) = 9.8 m/s²
2. Calculate the Weight of the Rocket:
- Weight (W) = mass × gravitational acceleration (g)
- Here, g=9.8m/s2
- Thus, W=m⋅g=25kg⋅9.8m/s2=245N
3. Determine the Thrust Force Required:
- According to Newton's second law, the net force acting on the rocket must equal the mass of the rocket times the acceleration.
- The thrust force (T) must overcome both the weight of the rocket and provide the necessary upward acceleration:
T=m⋅a+W
- Substituting the values:
T=25kg⋅9.8m/s2+245N=245N+245N=490N
4. Relate Thrust to Fuel Burn Rate:
- The thrust produced by the rocket can also be expressed in terms of the exhaust velocity and the rate of fuel consumption (dmdt):
T=v⋅dmdt
- Rearranging gives us the fuel burn rate:
dmdt=Tv
5. Substitute the Values:
- Now substitute the thrust (T = 490 N) and exhaust velocity (v = 2800 m/s):
dmdt=490N2800m/s=0.175kg/s
6. Conclusion:
- The rate at which the fuel must burn is 0.175kg/s.
Final Answer:
The fuel must burn at a rate of 0.175 kg/s.
- Mass of the rocket (m) = 25 kg
- Exhaust velocity of gases (v) = 28×102 m/s = 2800 m/s
- Required acceleration (a) = 9.8 m/s²
- Weight (W) = mass × gravitational acceleration (g)
- Here, g=9.8m/s2
- Thus, W=m⋅g=25kg⋅9.8m/s2=245N
- According to Newton's second law, the net force acting on the rocket must equal the mass of the rocket times the acceleration.
- The thrust force (T) must overcome both the weight of the rocket and provide the necessary upward acceleration:
T=m⋅a+W
- Substituting the values:
T=25kg⋅9.8m/s2+245N=245N+245N=490N
- The thrust produced by the rocket can also be expressed in terms of the exhaust velocity and the rate of fuel consumption (dmdt):
T=v⋅dmdt
- Rearranging gives us the fuel burn rate:
dmdt=Tv
- Now substitute the thrust (T = 490 N) and exhaust velocity (v = 2800 m/s):
dmdt=490N2800m/s=0.175kg/s
- The rate at which the fuel must burn is 0.175kg/s.
The fuel must burn at a rate of 0.175 kg/s.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
For a Rocket propulsion velocity of exhaust gases relative to rocket is 2km/s. If mass of rocket system is 1000 kg, then the rate of fuel consumption for a rockt to rise up with acceleration 4.9m/s2 will be:-
View SolutionA rocket of mass 1000 kg is to be projected vertically upwards. The gases are exhausted vertically downwards with velocity 100m/s with respect to the rocket. (What is the minimum rate of burning fuel, so as to just lift the rocket upwards against the gravitational attraction?) (Take g=10m/s2)
View SolutionA rocket of mass 40kg has 160kg fuel. The exhaust velocity of the fuel is 2.0km/s. The rate of consumption of fuel is 4kg/s. Calculate the ultimate vertical speed gained by the rocket. (g=10m/s2)
View Solution(a) A rocket set for vertical firing weighs 50kg and contains 450kg of fuel. It can have a maximum exhaust velocity of 2km/s. What should be its minimum rate of fuel consumption
(i) to just lift off the launching pad?
(ii) to give it an initial acceleration of 20m/s2?
(b) What will be the speed of the rocket when the rate of consumption of fuel is 10kg/s after whole of the fuel is consumed? (Take g=9.8m/s2)
View SolutionA rocket of mass 4000 kg is set for vertical firing. How much gas must be ejected per second so that the rocket may have initial upwards acceleration of magnitude 19.6m/s2 ? [Exhaust speed of fuel=980m/s]
View SolutionA diwali rocket moves vertically up with a constant acceleration a1=20//3ms−2. After sometives, its fuel gers exhausted ad then if falls freely with an acceleration a2=10ms−2, If themaximum height attained by the diwalin rocket is (h), using graphicalmerhod, find its speed when the fuel is just exausted. Assume h=50m.
View SolutionA rocket of mass 20000 kg is ejecting the gases at the rate of 50 kg/sec with speed of 20 m/sec in gravity free space. Find the acceleration of rocket at 2 sec.
View SolutionA ladder is hanging from ceiling as shownin figure. Three men A, B and C of masses 40 kg, 60 kg, and 50 kg are climbing the ladder. Man A is going up with retardation 2m/s2, C is going up with an acceleration of 1m/s2 and man B is going up with a constantg speed of 0.5 m/s. Find the tension in the string supporting the ledder. [g=9.8m/s2]

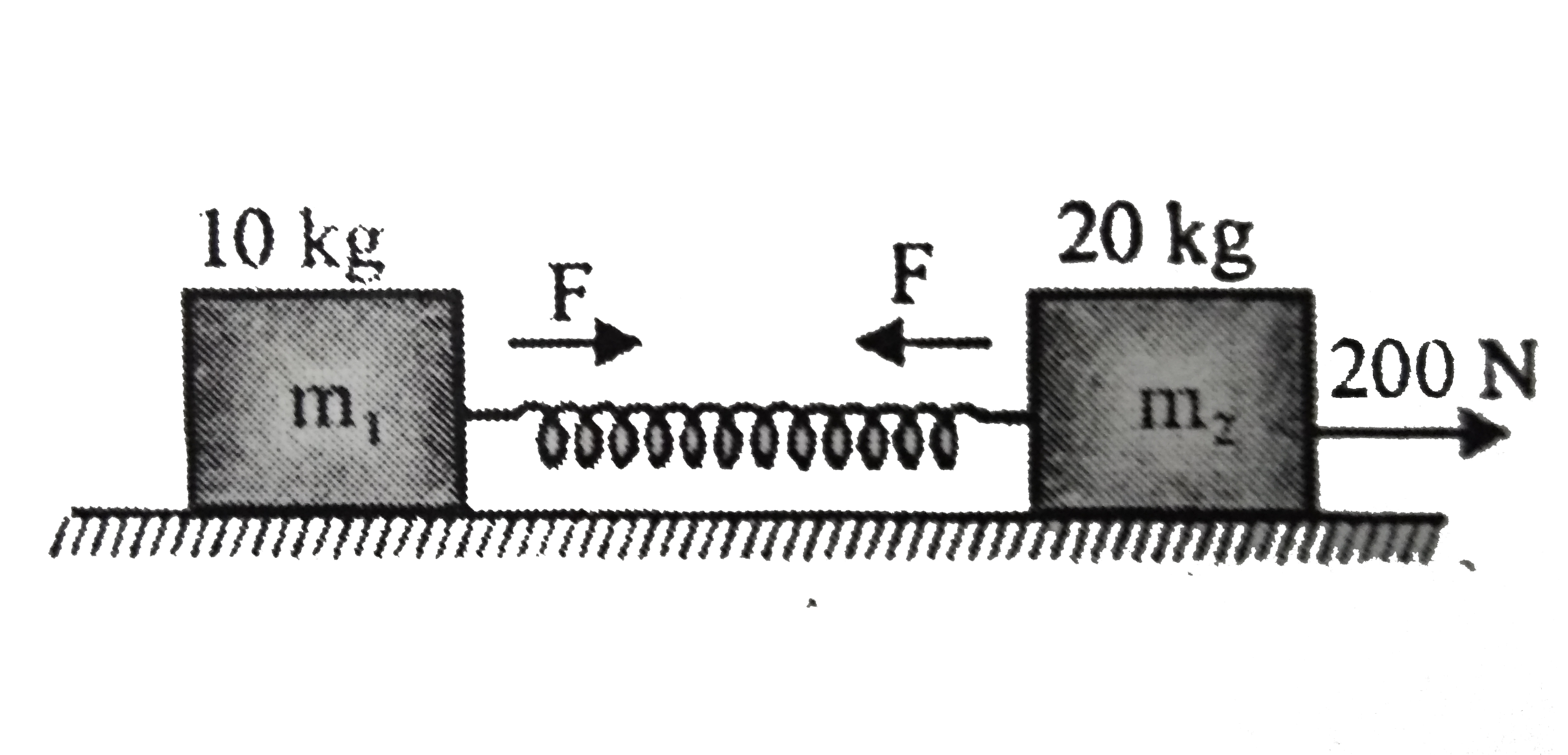
View SolutionTwo masses 10 kg and 20 kg respectively are connected by a massless spring as shown in figure force of 200 N acts on the 20 kg mass. At the instant shown is figure the 10 kg mass has acceleration of 12m/s2 what is the acceleration of 20 kg mass?
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View Solution
