The acceleration of a particle moving along x-axis is a=−100x+50. It is released from x=2. Here a and x are in S.I units. The motion of particle will be:
periodic, oscillatory but not SHM
periodic but not oscillatory
oscillatory but not periodic
simple harmonic
The correct Answer is:D
To solve the problem, we need to analyze the given acceleration equation and determine the nature of the motion of the particle.
1. Understand the Given Information:
The acceleration of the particle is given by the equation:
a=−100x+50
The particle is released from the position x=2.
2. Rearranging the Acceleration Equation:
We can rearrange the acceleration equation to isolate the terms involving x:
a−50=−100x
This can be rewritten as:
a=−100x+50
3. Analyzing the Form of the Acceleration:
The equation can be expressed as:
a=−100x+50
This indicates that the acceleration a depends linearly on the position x.
4. Identifying the Characteristics of Motion:
The acceleration is proportional to the negative of the displacement x (after rearranging), which suggests that the particle experiences a restoring force towards a fixed point. This is a characteristic of Simple Harmonic Motion (SHM).
5. Criteria for Simple Harmonic Motion:
For a motion to be classified as SHM, the following conditions must be satisfied:
- The acceleration must be directly proportional to the displacement from an equilibrium position.
- The acceleration must always act towards the equilibrium position.
6. Conclusion:
Since the acceleration a can be expressed as:
a=−100x+50
and the term −100x indicates that the acceleration is directed towards the origin (or a fixed point), we conclude that the motion of the particle is indeed Simple Harmonic Motion (SHM).
Final Answer:
The motion of the particle will be Simple Harmonic Motion (SHM).
The acceleration of the particle is given by the equation:
a=−100x+50
The particle is released from the position x=2.
We can rearrange the acceleration equation to isolate the terms involving x:
a−50=−100x
This can be rewritten as:
a=−100x+50
The equation can be expressed as:
a=−100x+50
This indicates that the acceleration a depends linearly on the position x.
The acceleration is proportional to the negative of the displacement x (after rearranging), which suggests that the particle experiences a restoring force towards a fixed point. This is a characteristic of Simple Harmonic Motion (SHM).
For a motion to be classified as SHM, the following conditions must be satisfied:
- The acceleration must be directly proportional to the displacement from an equilibrium position.
- The acceleration must always act towards the equilibrium position.
Since the acceleration a can be expressed as:
a=−100x+50
and the term −100x indicates that the acceleration is directed towards the origin (or a fixed point), we conclude that the motion of the particle is indeed Simple Harmonic Motion (SHM).
The motion of the particle will be Simple Harmonic Motion (SHM).
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Energy & spring pendulum)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Oscillations) (Simple pendulum and types of SHM)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Thermodynamic process)
20 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
The acceleration of a particle is a=−100x+50. It is released from x=2. Here, a and x are in SI units
View Solutionx-t equation of a particle moving along x-axis is given as
x=A+A(1−cosωt)
View SolutionFor a particle moving along the x-axis, mark the correct statement(s).
View SolutionThe position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionA particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
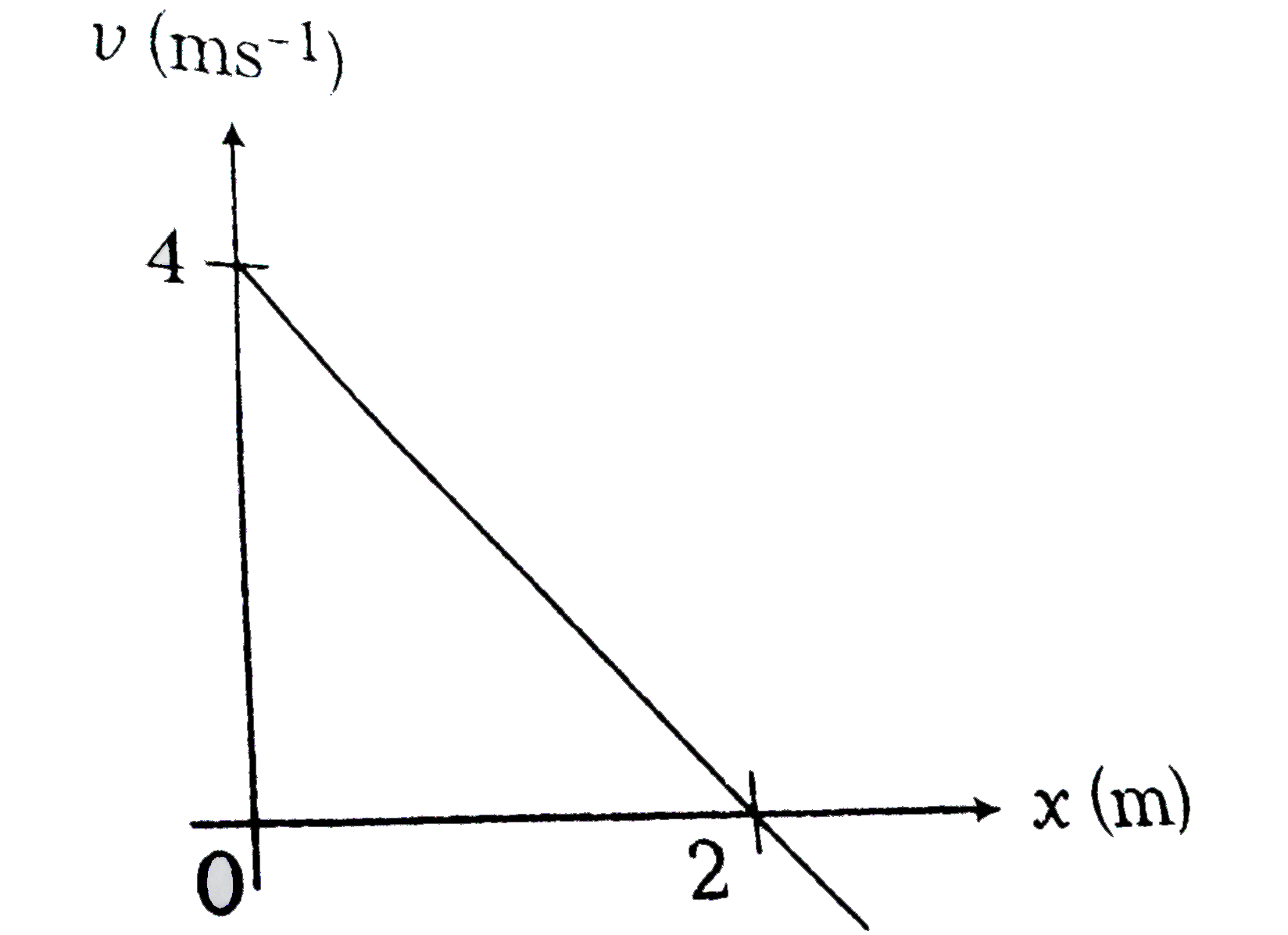
View SolutionFor a particle moving along x−axis, speed must be increasing for the following graph :
View Solutionx-coordinate of a particle moving along this axis is x=(2+t2+2t3). Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at t=2s.
View SolutionA particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View Solution
