An electric field E=(20ˆi+30ˆj) N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at (2m,2m).
To find the electric potential at the point (2 m, 2 m) given the electric field E=(20^i+30^j) N/C and the potential at the origin is zero, we can follow these steps:
1. Identify the Electric Field and the Point of Interest:
The electric field is given as:
E=20^i+30^jN/C
The point of interest is P(2m,2m).
2. Define the Position Vectors:
The position vector of the origin O is:
rO=0^i+0^j
The position vector of point P is:
rP=2^i+2^j
3. Calculate the Change in Position Vector:
The change in position vector Δr from the origin to point P is:
Δr=rP−rO=(2^i+2^j)−(0^i+0^j)=2^i+2^j
4. Use the Formula for Electric Potential Difference:
The potential difference V between two points in an electric field is given by:
V=VO−E⋅Δr
Since the potential at the origin VO=0, we have:
VP=−E⋅Δr
5. Calculate the Dot Product:
Now, we compute the dot product E⋅Δr:
E⋅Δr=(20^i+30^j)⋅(2^i+2^j)=(20×2)+(30×2)=40+60=100
6. Calculate the Potential at Point P:
Substitute the dot product back into the potential equation:
VP=−100V
Final Answer:
The potential at the point (2m,2m) is:
VP=−100V
The electric field is given as:
E=20^i+30^jN/C
The point of interest is P(2m,2m).
The position vector of the origin O is:
rO=0^i+0^j
The position vector of point P is:
rP=2^i+2^j
The change in position vector Δr from the origin to point P is:
Δr=rP−rO=(2^i+2^j)−(0^i+0^j)=2^i+2^j
The potential difference V between two points in an electric field is given by:
V=VO−E⋅Δr
Since the potential at the origin VO=0, we have:
VP=−E⋅Δr
Now, we compute the dot product E⋅Δr:
E⋅Δr=(20^i+30^j)⋅(2^i+2^j)=(20×2)+(30×2)=40+60=100
Substitute the dot product back into the potential equation:
VP=−100V
The potential at the point (2m,2m) is:
VP=−100V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An electric field E=(20ˆi+30ˆj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionAn electric field →E=−−−−−−−→i20+→j30NC−1 exists in the space. If the potential at the origin is taken to be zero find the potential at (2m, 2m).
View SolutionAn electric field →E=20yˆj exist in space . The potential at (5 m, 5 m) is taken to be zero. The potential at origin is
View SolutionAn electric field →E=→IAx exists in the space, where A=10Vm−2. Take the potential at (10m, 20m ) to be zero. Find the potential at the origin.
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
View SolutionA uniform field of 8 N/C exists in space in positive x-direction.
(a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z).
(b) At which points, the potential is 160 V ?
(c) It the potential at the origin is taken to be 80V, what will be the expression for the potential at a general point ?
(d) What will be the potential at the origin if the potential at x = infinity is taken to be zero ?
View SolutionElectrostatic field in a region is given by , vecE= (yzhati + zxhatj + xyhatk)V/m , where x,y and z are in m. If electric potential at origin is zero, then potential at (1m,1m, 1m) is
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
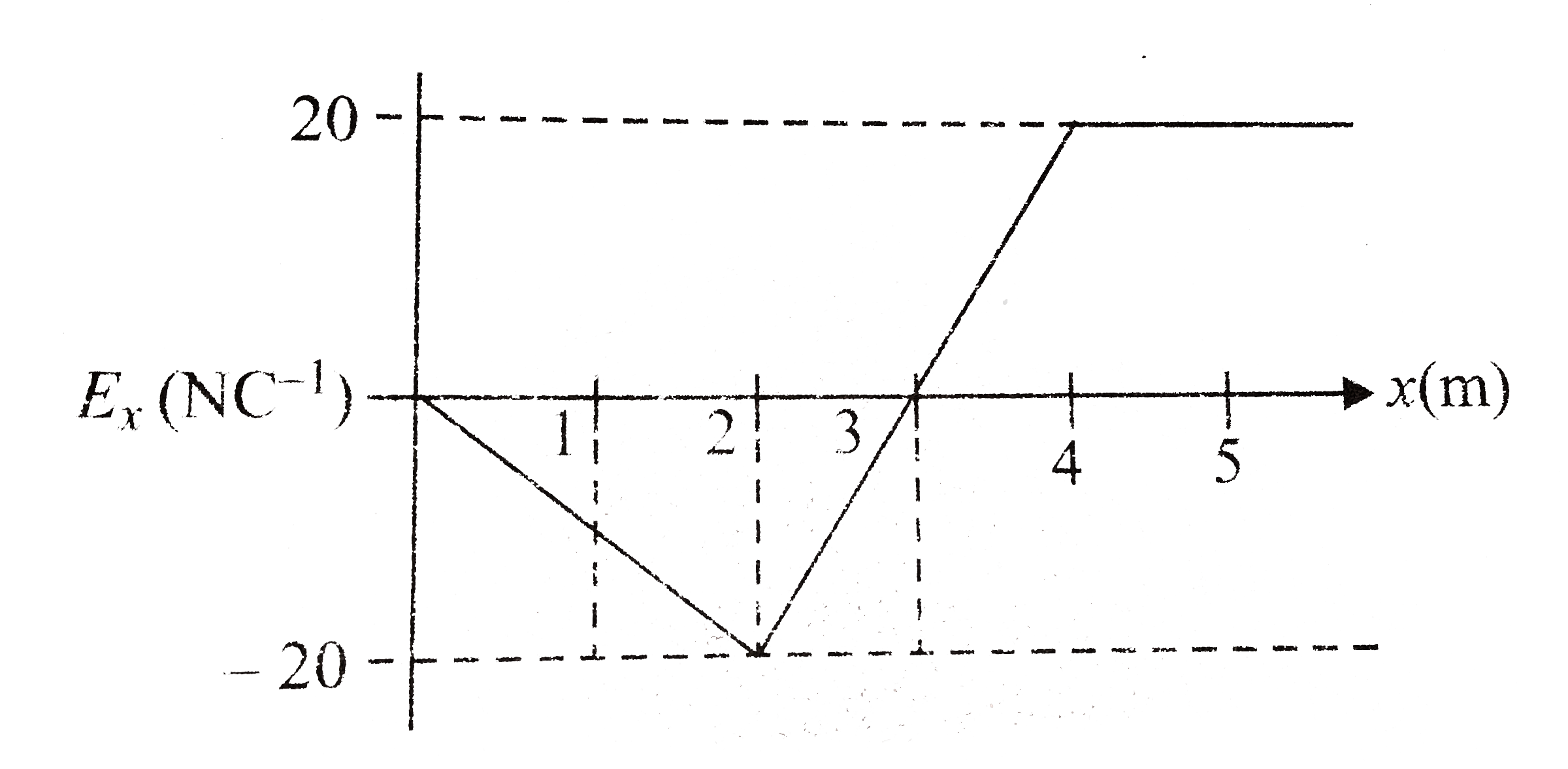
View Solution
