A light beam of wavelength incident on a silver sphere of radius r. suspended by a nonconducting thread. Find potentical aquired by sphere
None of these
To find the potential acquired by a silver sphere of radius r when a light beam of wavelength λ is incident on it, we can follow these steps:
Step 1: Understand the Photoelectric Effect
The question relates to the photoelectric effect, where incident light can cause electrons to be emitted from a material. The energy of the incident photons must be greater than the work function of the material for this to occur.
Step 2: Calculate the Energy of the Incident Photons
The energy E of a photon is given by the formula:
E=hcλ
where h is Planck's constant and c is the speed of light.
Step 3: Identify the Work Function
Let ϕ be the work function of silver. The threshold wavelength λ0 is related to the work function by:
ϕ=hcλ0
where λ0 is the threshold wavelength for the photoelectric effect.
Step 4: Determine the Maximum Kinetic Energy of Emitted Electrons
The maximum kinetic energy K.E. of the emitted electrons can be expressed as:
K.E.=E−ϕ
Substituting the expressions for E and ϕ:
K.E.=hcλ−hcλ0
Step 5: Relate Kinetic Energy to Potential
The kinetic energy of the emitted electrons can also be expressed in terms of the potential V acquired by the sphere:
K.E.=eV
where e is the charge of an electron. Thus, we can equate the two expressions for kinetic energy:
eV=hcλ−hcλ0
Step 6: Solve for the Potential V
Rearranging the equation gives:
V=hce(1λ−1λ0)
Final Result
The potential acquired by the sphere is:
V=hce(1λ−1λ0)
The question relates to the photoelectric effect, where incident light can cause electrons to be emitted from a material. The energy of the incident photons must be greater than the work function of the material for this to occur.
The energy E of a photon is given by the formula:
E=hcλ
where h is Planck's constant and c is the speed of light.
Let ϕ be the work function of silver. The threshold wavelength λ0 is related to the work function by:
ϕ=hcλ0
where λ0 is the threshold wavelength for the photoelectric effect.
The maximum kinetic energy K.E. of the emitted electrons can be expressed as:
K.E.=E−ϕ
Substituting the expressions for E and ϕ:
K.E.=hcλ−hcλ0
The kinetic energy of the emitted electrons can also be expressed in terms of the potential V acquired by the sphere:
K.E.=eV
where e is the charge of an electron. Thus, we can equate the two expressions for kinetic energy:
eV=hcλ−hcλ0
Rearranging the equation gives:
V=hce(1λ−1λ0)
The potential acquired by the sphere is:
V=hce(1λ−1λ0)
Topper's Solved these Questions
Similar Questions
A monochromatic light of wavelength λ is incident on an isolated metallic sphere of radius a. The threshold wavelength is λ0 which is larger than λ. Find the number of photoelectrons emitted before the emission of photoelectrons will stop.
View SolutionA conducting sphere of radius r has a charge . Then .
View SolutionIn the path of a uniform light beam of large cross-sectional area and intensity I. a solid sphere of redius R which is perfectly reflecting is placed . Find the force exerted on this sphere due to the light beam.
View SolutionFind the volume of the larges cylinder that can be inscribed in a sphere of radius r
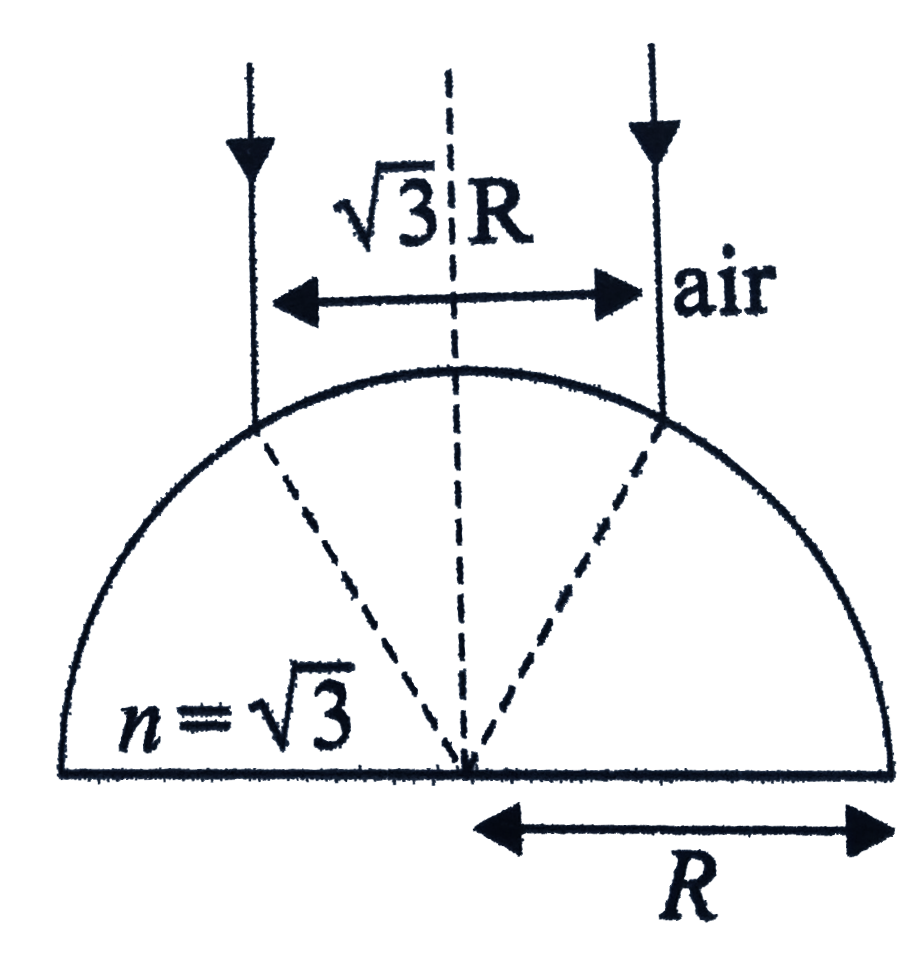
View SolutionA light beam of diameter √3R is incident symmetrically on a glass hemisphere of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemisphere.
View SolutionA charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.

View SolutionFind the number of sphere of radius r touching the coordinate axes.
View SolutionFind the number of sphere of radius r touching the coordinate axes.
View SolutionFind the volume of the largest cylinder that can be inscribed in a sphere of radius r
View SolutionWhen light of wavelength λ is incident on photosensitive surface, the stopping potential is V. When light of wavelength 3λ is incident on same surface, the stopping potential is V6 Threshold wavelength for the surface is
View Solution