A particle is movin along straight line such that dot product of its acceleration →a and velocity →v is negative. How many times particle can be found at a distance d from the origin?
One
Three
Two
Can't be determined with given data
The correct Answer is:D
To solve the problem, we need to analyze the motion of the particle given that the dot product of its acceleration →a and velocity →v is negative. This implies that the angle θ between the vectors →a and →v is greater than 90 degrees.
1. Understanding the Dot Product:
The dot product of two vectors is given by:
→a⋅→v=|→a||→v|cos(θ)
Since the dot product is negative, we have:
cos(θ)<0⟹θ>90∘
This means that the acceleration is acting in the opposite direction to the velocity.
2. Implication of Negative Dot Product:
When the acceleration is opposite to the velocity, it means that the particle is decelerating. The particle will eventually come to a stop when its velocity becomes zero.
3. Motion Analysis:
Let's denote the initial position of the particle as x0 and the distance from the origin as d. As the particle moves, it will decelerate until it stops. After reaching the maximum displacement, it will start moving back towards the origin.
4. Determining the Path:
The particle can be found at a distance d from the origin twice:
- Once while moving away from the origin (before it stops).
- Once while returning back towards the origin (after it has reversed direction).
5. Conclusion:
Since the particle can reach the distance d twice during its motion (once while moving away and once while returning), the answer to the question is:
The particle can be found at a distance d from the origin 2 times.
The dot product of two vectors is given by:
→a⋅→v=|→a||→v|cos(θ)
Since the dot product is negative, we have:
cos(θ)<0⟹θ>90∘
This means that the acceleration is acting in the opposite direction to the velocity.
When the acceleration is opposite to the velocity, it means that the particle is decelerating. The particle will eventually come to a stop when its velocity becomes zero.
Let's denote the initial position of the particle as x0 and the distance from the origin as d. As the particle moves, it will decelerate until it stops. After reaching the maximum displacement, it will start moving back towards the origin.
The particle can be found at a distance d from the origin twice:
- Once while moving away from the origin (before it stops).
- Once while returning back towards the origin (after it has reversed direction).
Since the particle can reach the distance d twice during its motion (once while moving away and once while returning), the answer to the question is:
The particle can be found at a distance d from the origin 2 times.
Similar Questions
The speed of a particle moving in a circle is increasing. The dot product of its acceleration and velocity is
View SolutionFor a particle moving in straight line with increasing speed the appropriate sign of acceleration a and velocity v can be:
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
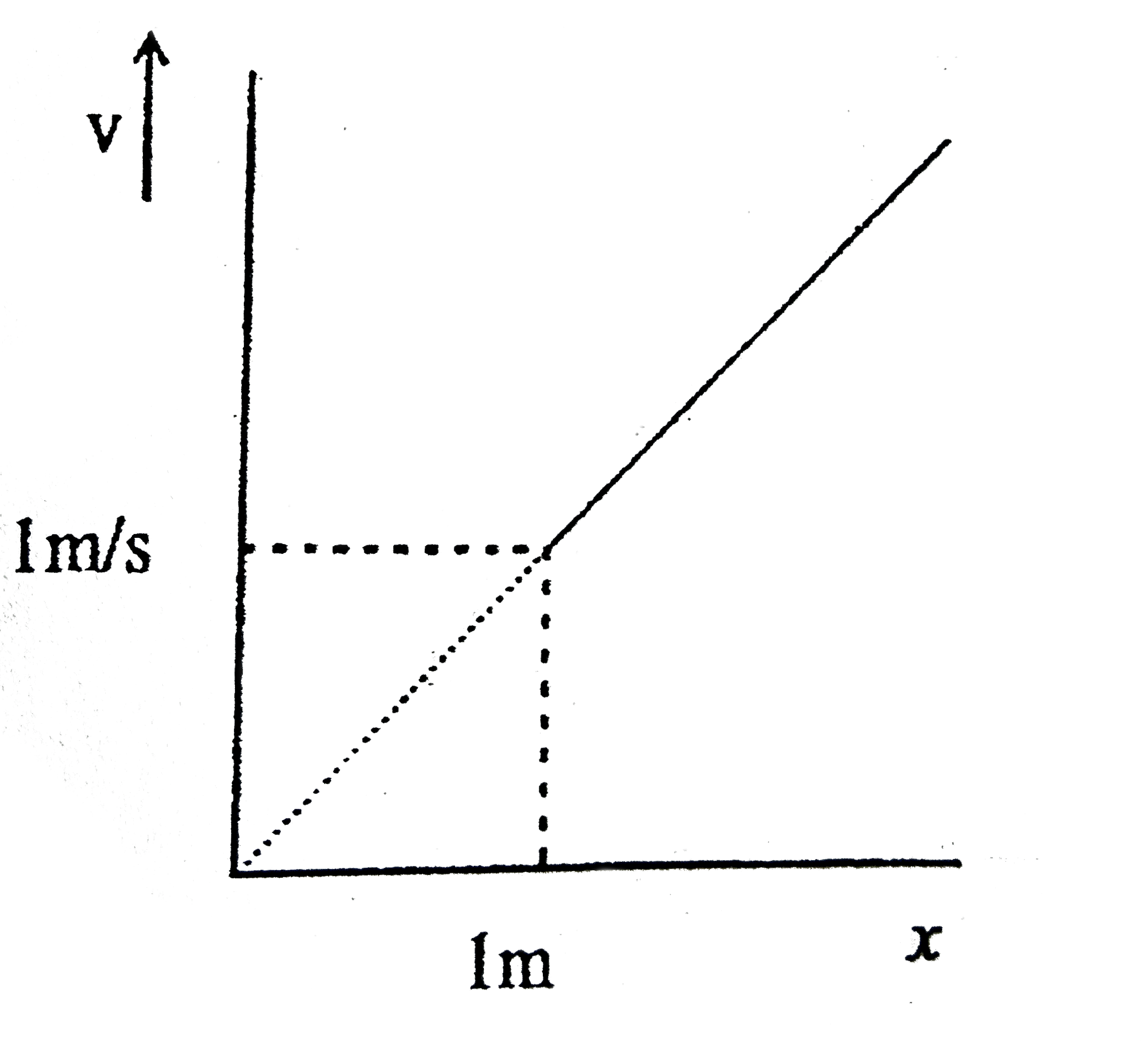
View SolutionA particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and tenth second it travels a distance od 10m. Then the acceleration of the particle will be.
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View Solution
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positive
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View SolutionA particle moving along a straight line with initial velocity u and acceleration a continues its motion for n seconds. What is the distance covered by it in the last nth second ?
View Solution
