For a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
R√5
R√2
R
R√2
To solve the problem of finding the distance h from the center of a uniformly charged ring where the electric field on its axis has the largest magnitude, we can follow these steps:
1. Understand the Electric Field of a Charged Ring:
The electric field E at a distance h along the axis of a uniformly charged ring of radius R and total charge Q is given by the formula:
E=kQh(h2+R2)3/2
where k is Coulomb's constant.
2. Differentiate the Electric Field with Respect to h:
To find the maximum electric field, we need to differentiate E with respect to h and set the derivative equal to zero:
dEdh=0
3. Apply the Quotient Rule:
Using the quotient rule for differentiation, we differentiate E:
dEdh=(h2+R2)3/2⋅kQ−kQh⋅32(h2+R2)1/2⋅2h(h2+R2)3
Simplifying this gives:
dEdh=kQ((h2+R2)3/2−3h2(h2+R2)1/2)(h2+R2)3
4. Set the Derivative Equal to Zero:
Setting the numerator equal to zero for maximization:
(h2+R2)3/2−3h2(h2+R2)1/2=0
This simplifies to:
(h2+R2)−3h2=0
which leads to:
R2−2h2=0⇒R2=2h2
5. Solve for h:
Rearranging gives:
h2=R22⇒h=R√2
6. Conclusion:
The distance h from the center of the ring where the electric field is maximized is:
h=R√2
Final Answer:
h=R√2
The electric field E at a distance h along the axis of a uniformly charged ring of radius R and total charge Q is given by the formula:
E=kQh(h2+R2)3/2
where k is Coulomb's constant.
To find the maximum electric field, we need to differentiate E with respect to h and set the derivative equal to zero:
dEdh=0
Using the quotient rule for differentiation, we differentiate E:
dEdh=(h2+R2)3/2⋅kQ−kQh⋅32(h2+R2)1/2⋅2h(h2+R2)3
Simplifying this gives:
dEdh=kQ((h2+R2)3/2−3h2(h2+R2)1/2)(h2+R2)3
Setting the numerator equal to zero for maximization:
(h2+R2)3/2−3h2(h2+R2)1/2=0
This simplifies to:
(h2+R2)−3h2=0
which leads to:
R2−2h2=0⇒R2=2h2
Rearranging gives:
h2=R22⇒h=R√2
The distance h from the center of the ring where the electric field is maximized is:
h=R√2
h=R√2
Similar Questions
In a uniformly charged sphere of total charge Q and radius R, the electric field E is plotted as function of distance from the centre, The graph which would correspond to the above will be:
View SolutionConsider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
View SolutionThe largest magnitude the electric field on the axis of a uniformly charged ring of radius 3m is at a distance h from its centre. What is the value of h? (Take 1√2=0.7)
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionAt which distance along the centre axis of a uniformaly charged plastic disc of radius R is the magnitude of the electric field equal to one-half the magnitude of the field at the centre of the surface of the disc ?
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
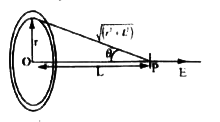
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA charged disc of radius 3 m has charge density σ. Electric field at a distance of 4 m from its centre on axis is _______
View Solution