Consider a piston- cylinder arrangement with spring in its natural length. Due to heat transfer, the gas expands until the piston hits the stop. The mass of piston is 10kg and area is 78cm2. Initial and final specific internal energies are 214 and 337kJ/kg
Initial pressure of gas is 112k Pa
Work done by gas on the piston is 56.5J
Work done by gas on the piston is 100J
Heat transfer for 0.5 gas is 118J
The correct Answer is:A, B, D
To solve the problem involving a piston-cylinder arrangement with a spring, we need to analyze the given data and apply the principles of thermodynamics.
Given Data:
- Mass of the piston, m=10kg
- Area of the piston, A=78cm2=78×10−4m2=0.0078m2
- Initial specific internal energy, u1=214kJ/kg=214000J/kg
- Final specific internal energy, u2=337kJ/kg=337000J/kg
Step 1: Calculate the change in internal energy per unit mass
The change in specific internal energy Δu can be calculated as:
Δu=u2−u1=337000J/kg−214000J/kg=123000J/kg
Step 2: Calculate the total change in internal energy for the piston
To find the total change in internal energy for the piston, we need to multiply the change in specific internal energy by the mass of the gas inside the cylinder. However, we need to find the mass of the gas first.
Assuming the gas is ideal and using the ideal gas law, we can express the mass of the gas in terms of its specific internal energy and the volume it occupies. For this problem, we will focus on the energy change.
Step 3: Calculate the work done by the gas
The work done W by the gas during the expansion can be calculated using the formula:
W=PΔV
Where P is the pressure and ΔV is the change in volume. The pressure can be calculated using the force exerted by the piston divided by the area of the piston.
Step 4: Calculate the force exerted by the piston
The force F exerted by the piston due to its weight is given by:
F=m⋅g=10kg⋅9.81m/s2=98.1N
Step 5: Calculate the pressure exerted by the piston
The pressure P exerted by the piston can be calculated as:
P=FA=98.1N0.0078m2≈12500Pa
Step 6: Calculate the work done by the gas
Assuming the volume change is significant, we can express ΔV in terms of the area and the distance moved by the piston. However, since the piston hits the stop, we can consider the work done as:
W=P⋅V
Where V can be approximated based on the area and the stroke length of the piston.
Step 7: Apply the first law of thermodynamics
According to the first law of thermodynamics:
ΔU=Q−W
Where ΔU is the change in internal energy, Q is the heat added, and W is the work done by the system.
Step 8: Solve for heat added
Rearranging the equation gives:
Q=ΔU+W
Conclusion
To find the exact values for Q and W, we would need more information about the volume change or the specific heat capacities of the gas involved. However, the steps outlined provide a framework for solving the problem based on the principles of thermodynamics.
- Mass of the piston, m=10kg
- Area of the piston, A=78cm2=78×10−4m2=0.0078m2
- Initial specific internal energy, u1=214kJ/kg=214000J/kg
- Final specific internal energy, u2=337kJ/kg=337000J/kg
The change in specific internal energy Δu can be calculated as:
Δu=u2−u1=337000J/kg−214000J/kg=123000J/kg
To find the total change in internal energy for the piston, we need to multiply the change in specific internal energy by the mass of the gas inside the cylinder. However, we need to find the mass of the gas first.
The work done W by the gas during the expansion can be calculated using the formula:
W=PΔV
Where P is the pressure and ΔV is the change in volume. The pressure can be calculated using the force exerted by the piston divided by the area of the piston.
The force F exerted by the piston due to its weight is given by:
F=m⋅g=10kg⋅9.81m/s2=98.1N
The pressure P exerted by the piston can be calculated as:
P=FA=98.1N0.0078m2≈12500Pa
Assuming the volume change is significant, we can express ΔV in terms of the area and the distance moved by the piston. However, since the piston hits the stop, we can consider the work done as:
W=P⋅V
Where V can be approximated based on the area and the stroke length of the piston.
According to the first law of thermodynamics:
ΔU=Q−W
Where ΔU is the change in internal energy, Q is the heat added, and W is the work done by the system.
Rearranging the equation gives:
Q=ΔU+W
To find the exact values for Q and W, we would need more information about the volume change or the specific heat capacities of the gas involved. However, the steps outlined provide a framework for solving the problem based on the principles of thermodynamics.
Similar Questions
A weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View Solution2.00 mole of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston. The piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is 300K at its natural length. the atmosphere pressure is 100 kPa. the gas is heated slowly for some time by means of an electric heater so as to move the position up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.
 View Solution
View SolutionMethod 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.
 View Solution
View SolutionA gas is enclosed in a cylindrical vessel fitted with a frictionless piston.the gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10cm. Find the increase in the internal energy of the gas, the area of cross section of the cylinder=4cm2 and the atmospheric pressure =100kPa.
View SolutionA container is closed by a movable piston. We supply heat to gas inside container. Due to heating, piston is displaced by 5 cm. cross section area of cylinder is 40 cm2 and heat supplied to gas is 40 joules. The change in internal energy is
 View Solution
View SolutionThe piston cylinder arrangement shown contains a diatomic gas at temperature 300 K The cross sectinal area of the cylinder is 1m2. Initially the height of the piston above th base of the cyclinder is 1 m. The temperature is now raised to 400 K at constant pressure. There is no heat loss in the process..
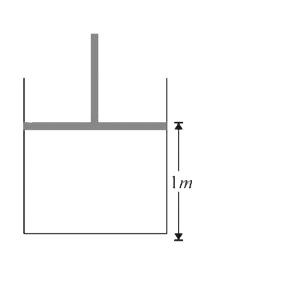
Find the new height (in m) of the piston above the base of the cylinder.View SolutionA fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
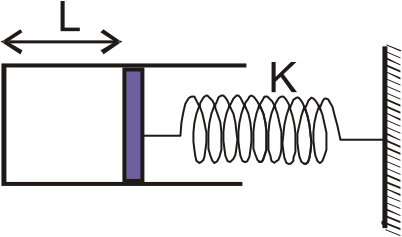 View Solution
View SolutionAir is contained in a piston-cylinder arrangement as shown in Fig. with a cross-sectional area of 4cm2 and an initial volume of 20cm3. The air is initially at a pressure of 1 atm and temperature of 20∘C. The piston is connected to a spring whose spring constant is k=104N/m, and the spring is initially underformed. How much heat must be added to the air inside cylinder to increase the pressure to 3 atm (for air, CV=718J/kg.∘C, molecular of air 28.97)?
 View Solution
View SolutionConsider a vertical tube open at both ends. The tube consistss of two parts, each of different cross sections and each part having a piston which can move smoothly in respective tubes. The two piston which can move smoothly in respective tube wire. The piston are joined together by an inextensible wire. The combined mass of the two piston is 5kgand area of cross section of the upper piston is 10cm2 greater than that of the lower piston. Amount of gas enclosed by the pistons is 1mol. When the gas is heated slowly, pistons move by 50cm. Find the rise in the temperature of the gas in the form X/RK, where R is universal gas constant. Use g=10m/s2 and outside pressure =105N/m2).
 View Solution
View SolutionConsider a vertical tube open at both ends. The tube consistss of two parts, each of different cross sections and each part having a piston which can move smoothly in respective tubes. The two piston which can move smoothly in respective tube wire. The piston are joined together by an inextensible wire. The combined mass of the two piston is 5kgand area of cross section of the upper piston is 10cm2 greater than that of the lower piston. Amount of gas enclosed by the pistons is 1mol. When the gas is heated slowly, pistons move by 50cm. Find the rise in the temperature of the gas in the form X/RK, where R is universal gas constant. Use g=10m/s2 and outside pressure =105N/m2).
 View Solution
View Solution

