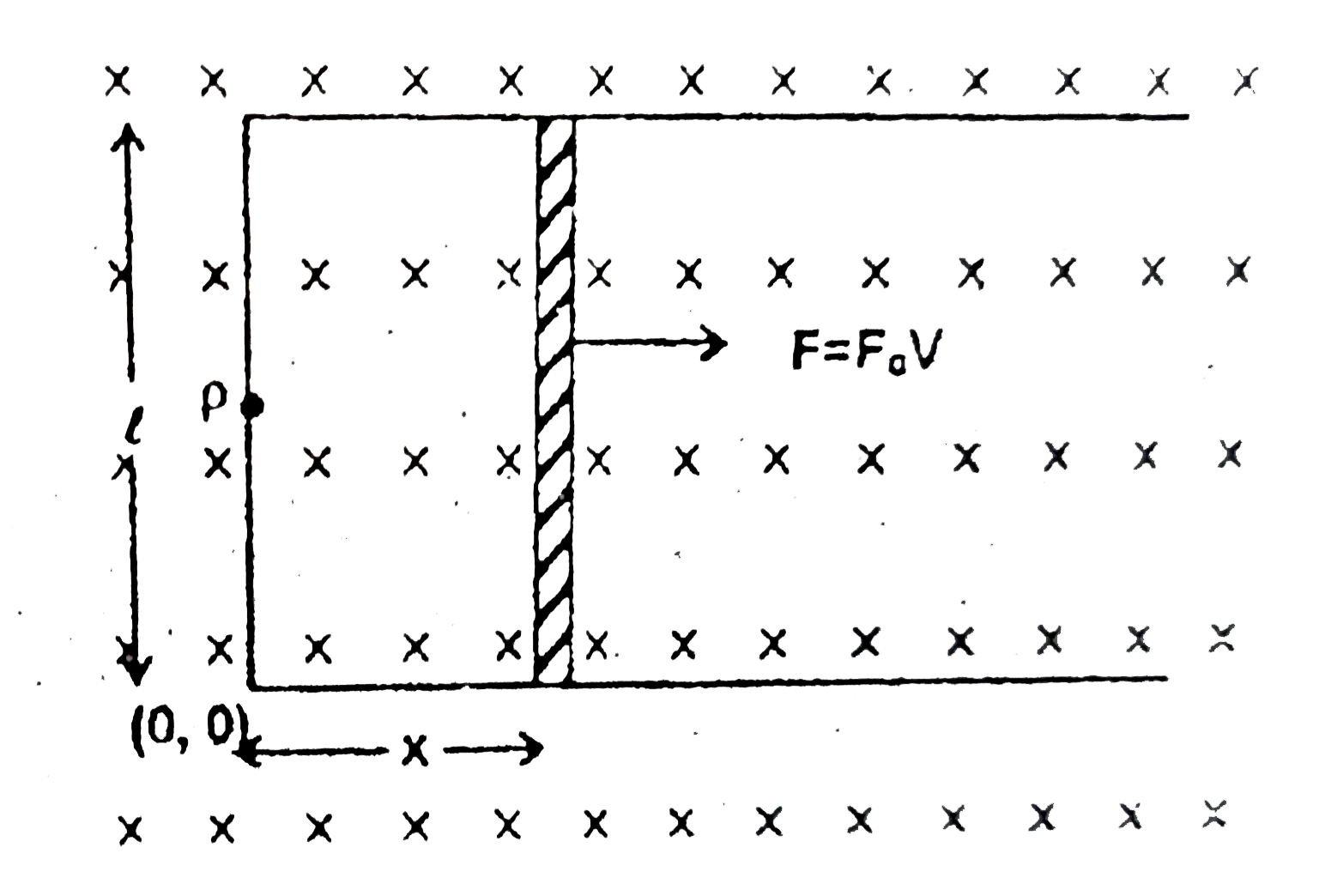
Two infinite parallel wire, having the cross sectional area 'a' and resistivity 'k' are connected at a junction point 'p' (as shown in the figure). A slide wire of negligible resistance and having mass 'm' and length 'l' can slide between the parallel wires, without any frictional resistance. If the system of wires is introduced to a magnetic field of intensity 'B' (into the plane of paper) and the slide wire is pulled with a force which varies with the velocity of the slide wire as F=F0v, then find the velocity of the slide wire as a function of the distance travelled.
(The slide wire is initially at origin and has a velocity v0)
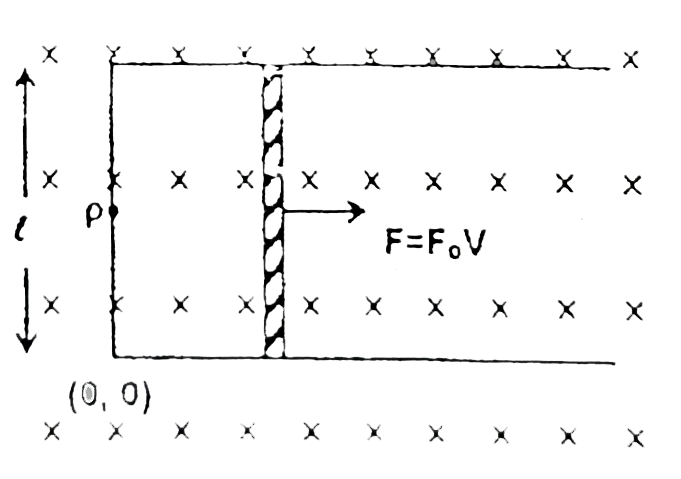
At any given instance of time the slide wire is at distance x from origin, then the resistance of the circuit is R=k(2x+l)a
If the velocity of slide wire is v, then the emf generated is Blv so we have
BlV−ka(2x+l)I=0
Or, I=Blak(v2x+l)
This current exerts magnetic force in the wire given by F'
So, F'=IlB=Blak(v2x+l)lB=B2l2ak(v2x+l)
Since, F−F'=mdvdt
So F0v−B2l2ak(v2x+l)=mvdvdx
⇒F0m−B2l2akm(12x+l)=dvdx
⇒∫x0[F0m−B2l2akm(12x+l)]dx=∫VV0dv
F0mx−B2l2a2km{ln(2x+ll)}+v0=v
Similar Questions
The resistance of wire ABC is double of resistance of wire ADC. The magnetic field at O is

View SolutionIn the given circuit diagram , a connecting wire of negligible resistance is joining the points B and D, the current in the connecting wire is
View SolutionA thin wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction , as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper , the wire takes the shape of a circle . The tension in the wire is
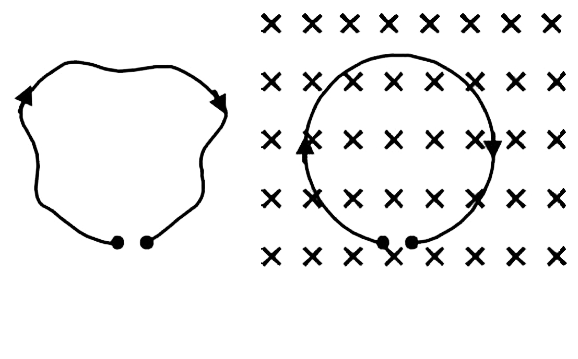
View SolutionA thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is :
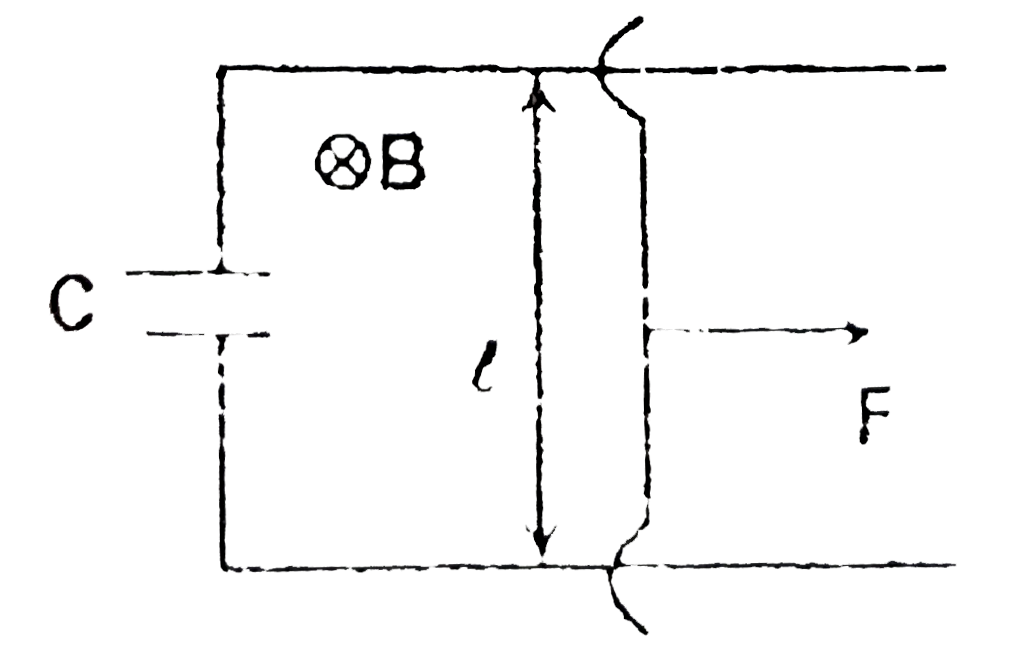
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
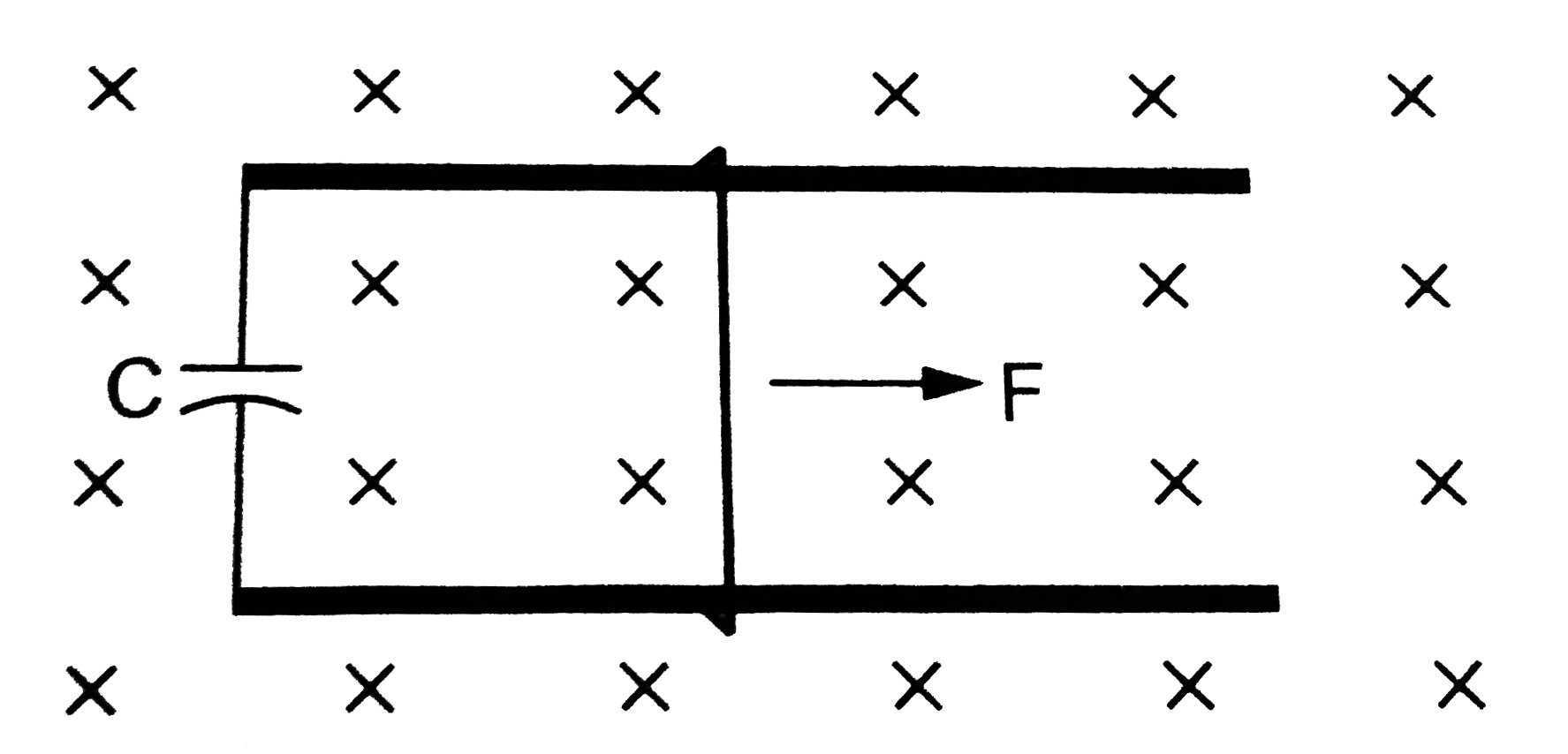
View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
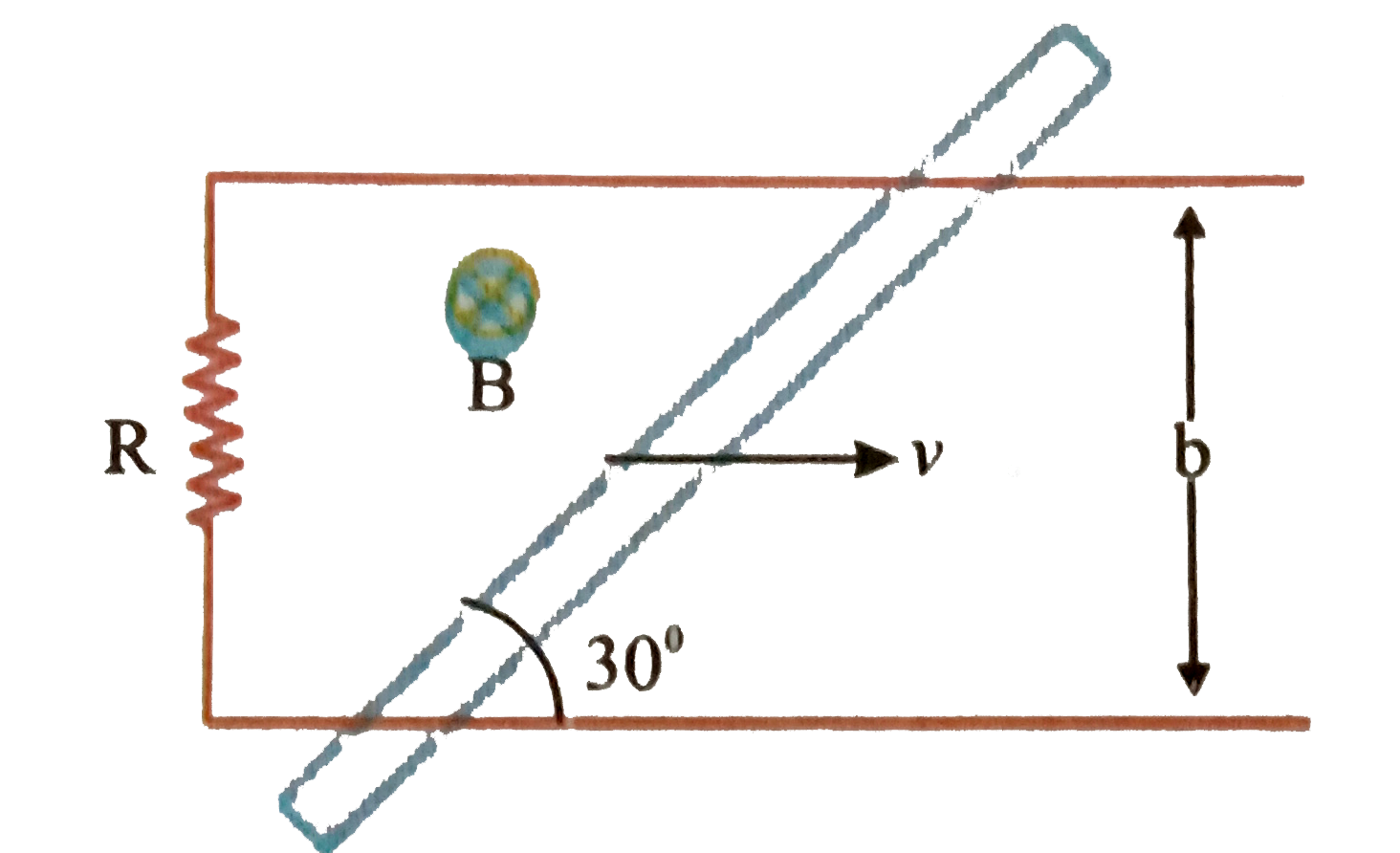
View SolutionA wire is sliding as shown in Figure. The angle between the acceleration and the velocity of the wire is
View SolutionIn the circuit shown below, the internal resistance of the cell is negligible. The distance of the slider from the left-hand end of the slide wire is l. The graph shows the variation with l of the current I in the cell.
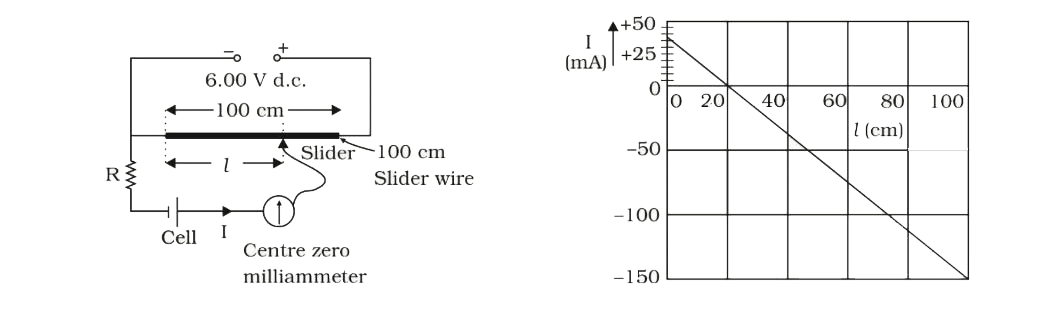
Value of the resistance R is:
View SolutionIn the circuit shown in figure, all wires have equal resistance r. Find the equivalent resistance between A and B
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. The whole system lies in amagnetic field B and a constant force F is applied to the rod . Then

View Solution
