A straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
To solve the problem, we need to find the minimum magnetic field B required to slide a straight wire of length l on two parallel rails with a coefficient of friction μ while carrying a current I.
1. Identify Forces Acting on the Wire:
- The wire experiences a magnetic force due to the current flowing through it in the presence of a magnetic field. This force can be expressed as:
Fmagnetic=I⋅l⋅B⋅sin(θ)
- Here, θ is the angle between the direction of the current and the magnetic field.
2. Frictional Force:
- The wire also experiences a frictional force opposing its motion, which is given by:
Ffriction=μ⋅Fnormal
- The normal force Fnormal acting on the wire is equal to its weight, which can be expressed as:
Fnormal=m⋅g
- Therefore, the frictional force becomes:
Ffriction=μ⋅m⋅g
3. Setting Up the Equation:
- For the wire to slide, the magnetic force must be equal to the frictional force:
I⋅l⋅B⋅sin(θ)=μ⋅m⋅g
4. Solving for Magnetic Field B:
- Rearranging the equation to solve for B:
B=μ⋅m⋅gI⋅l⋅sin(θ)
5. Finding Minimum Magnetic Field:
- To find the minimum magnetic field, we need to maximize sin(θ). The maximum value of sin(θ) is 1, which occurs when θ=90∘.
- Substituting sin(90∘)=1 into the equation gives:
Bmin=μ⋅m⋅gI⋅l
Final Answer:
The minimum magnetic field required to slide the wire on the rails is:
Bmin=μ⋅m⋅gI⋅l
- The wire experiences a magnetic force due to the current flowing through it in the presence of a magnetic field. This force can be expressed as:
Fmagnetic=I⋅l⋅B⋅sin(θ)
- Here, θ is the angle between the direction of the current and the magnetic field.
- The wire also experiences a frictional force opposing its motion, which is given by:
Ffriction=μ⋅Fnormal
- The normal force Fnormal acting on the wire is equal to its weight, which can be expressed as:
Fnormal=m⋅g
- Therefore, the frictional force becomes:
Ffriction=μ⋅m⋅g
- For the wire to slide, the magnetic force must be equal to the frictional force:
I⋅l⋅B⋅sin(θ)=μ⋅m⋅g
- Rearranging the equation to solve for B:
B=μ⋅m⋅gI⋅l⋅sin(θ)
- To find the minimum magnetic field, we need to maximize sin(θ). The maximum value of sin(θ) is 1, which occurs when θ=90∘.
- Substituting sin(90∘)=1 into the equation gives:
Bmin=μ⋅m⋅gI⋅l
The minimum magnetic field required to slide the wire on the rails is:
Bmin=μ⋅m⋅gI⋅l
Topper's Solved these Questions
Similar Questions
A long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
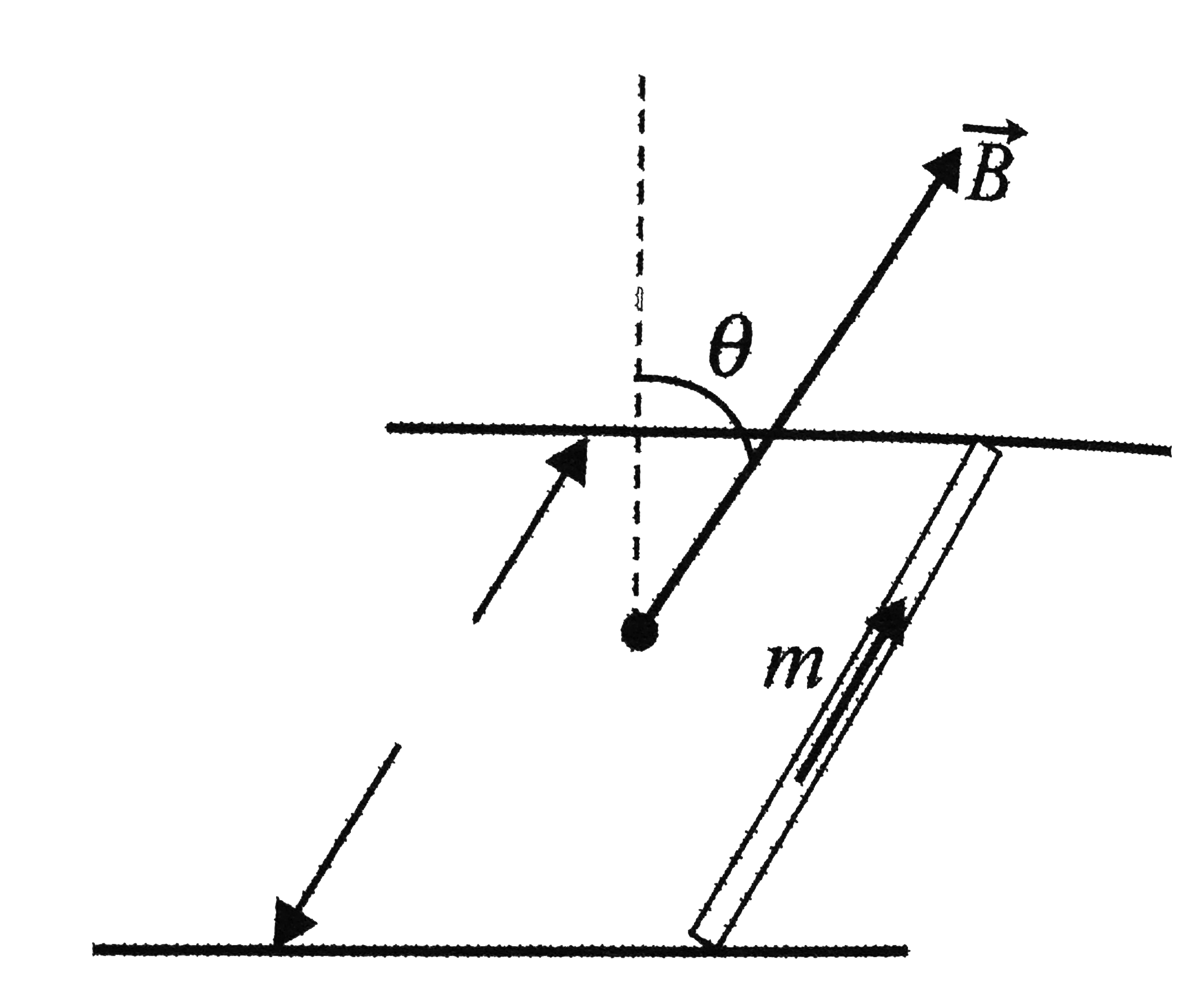
View Solution
Knowledge Check
A wire of length 1 m placed in x-z plane carries current of 1 amp. The coefficient of friction between wire and the surface is 0.2 and mass of the wire is 2. The magnetic field of strengh 2 T exists along position y direction . Then choose the correct statment .
AAcceleration of wire is 0.5m/s2BWire will not move at allCAccceleration of wire is m/s2DAcceleration of wire is 2m/s2A straight wire of length 0.5 m carrying a current of 1.6 ampere is placed in a uniform magnetic field of induction 2 T. If the magnetic field is perendicular to the length of the wire, then force on the wire is
A2.4 NB1.2 NC1.6 ND3.2 NThe intensity of uniform magnetic field between poles of a magnetic is H. If a straight wire carrying current is placed in between the poles. The direction of force on the wire is-
 Aperpendicular to both current and magnetic fieldBin the direction of currentCsame as magnetic fieldDin all directions
Aperpendicular to both current and magnetic fieldBin the direction of currentCsame as magnetic fieldDin all directions
A wire of length l metre carries a current I ampere along the Y-axis. A magnetic field, →B=B0(ˆi+ˆj+ˆk) tesla exists in space. Find the magnitude of the force on the wire.
View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

View SolutionFigure shows a wire of resistance R sliding on two parallel, conducting fixed thick rails placed at a separation l. A magnetic fild B exist in a direction perpendicular to the plane of the rails. The wire is moving with a constant velocity v. Find current through the wire
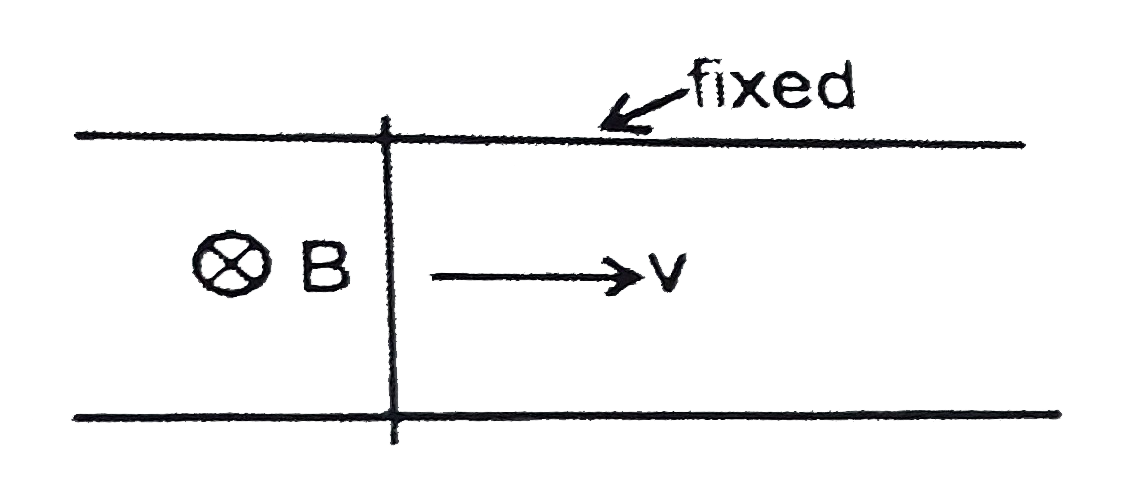
View SolutionTwo infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
View SolutionTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
View Solution
