Two identical rods of length (L), area of cross-sectional (A) and thermal conductivity k are joined end to end. If temperature difference of free ends is ΔT, the heat Q0 flows along rods per second. Find the total heat flowing per second along the rods if the two rods are placed parallel and temperature difference of free ends is ΔT. There is no heat loss from curved surface.
Q=4Q0
Q=2Q0
Q=Q0/4
Q=Q0/2
To solve the problem, we will analyze the heat flow through two identical rods when they are arranged in parallel.
1. Understanding Thermal Resistance:
Each rod has a thermal resistance R. The thermal resistance R for a rod can be calculated using the formula:
R=LkA
where L is the length of the rod, k is the thermal conductivity, and A is the cross-sectional area.
2. Heat Flow in Series:
When the two rods are connected end-to-end (in series), the total thermal resistance Rnet is the sum of the resistances:
Rnet=R1+R2=R+R=2R
The heat flow Q0 through the rods when they are in series is given by:
Q0=ΔTRnet=ΔT2R
3. Heat Flow in Parallel:
When the two rods are placed in parallel, the total thermal resistance Rnet can be calculated using the formula for parallel resistances:
1Rnet=1R1+1R2=1R+1R=2R
Therefore, the equivalent resistance is:
Rnet=R2
4. Calculating Total Heat Flow:
The total heat flow Q through the rods when they are in parallel is:
Q=ΔTRnet=ΔTR2=2ΔTR
5. Relating Q to Q0:
From the expression for Q0:
Q0=ΔT2R
We can express Q in terms of Q0:
Q=4×Q0
Final Answer:
Thus, the total heat flowing per second along the rods when placed in parallel is:
Q=4Q0
Each rod has a thermal resistance R. The thermal resistance R for a rod can be calculated using the formula:
R=LkA
where L is the length of the rod, k is the thermal conductivity, and A is the cross-sectional area.
When the two rods are connected end-to-end (in series), the total thermal resistance Rnet is the sum of the resistances:
Rnet=R1+R2=R+R=2R
The heat flow Q0 through the rods when they are in series is given by:
Q0=ΔTRnet=ΔT2R
When the two rods are placed in parallel, the total thermal resistance Rnet can be calculated using the formula for parallel resistances:
1Rnet=1R1+1R2=1R+1R=2R
Therefore, the equivalent resistance is:
Rnet=R2
The total heat flow Q through the rods when they are in parallel is:
Q=ΔTRnet=ΔTR2=2ΔTR
From the expression for Q0:
Q0=ΔT2R
We can express Q in terms of Q0:
Q=4×Q0
Thus, the total heat flowing per second along the rods when placed in parallel is:
Q=4Q0
Similar Questions
Three rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.
 View Solution
View SolutionThe ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
View Solution
Knowledge Check
- Question 1 - Select One
Two chunks of metal with heat capacities C1 and C2, are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t=0 the temperature difference betwene the two chunks of metal equals (ΔT)0. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time.
AT0exp(−KA(C1+C2)tC1C2)BT0exp(−KA(C1+C2)C1C2)CT0exp(KA(C1+C2)tC1C2)DT0exp(KA(C1+C2)t2C1C2)
The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
View SolutionFigure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.
 View Solution
View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
 View Solution
View SolutionTwo rods of same length and areas of cross section A1 and A2 have their ends at same temperature. If K1 and K2 are their thermal conductivities, C1 and C2 their specific heats and ρ1 and ρ2 are their densities, then the condition that rate of flow of heat is same in both the rods is
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.
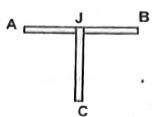
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.View SolutionTwo rods of same length and same material having area of cross section A and 4A respectively are joined as shown in the figure. If TA and TB are temperatures of free ends in steady state. The temperature of junction point C is (Assume no heat loss wil take place through lateral surface)
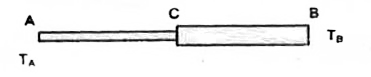 View Solution
View Solution

