A truck has to move to a dimetrically opposite point on a circular track which surrounds a field. The speed of the truck along the track is $2 v_{0}$ . While that in the field is $v_{0}$ . The driver plans to move along an arc of a circle and then along a straight line as shown.

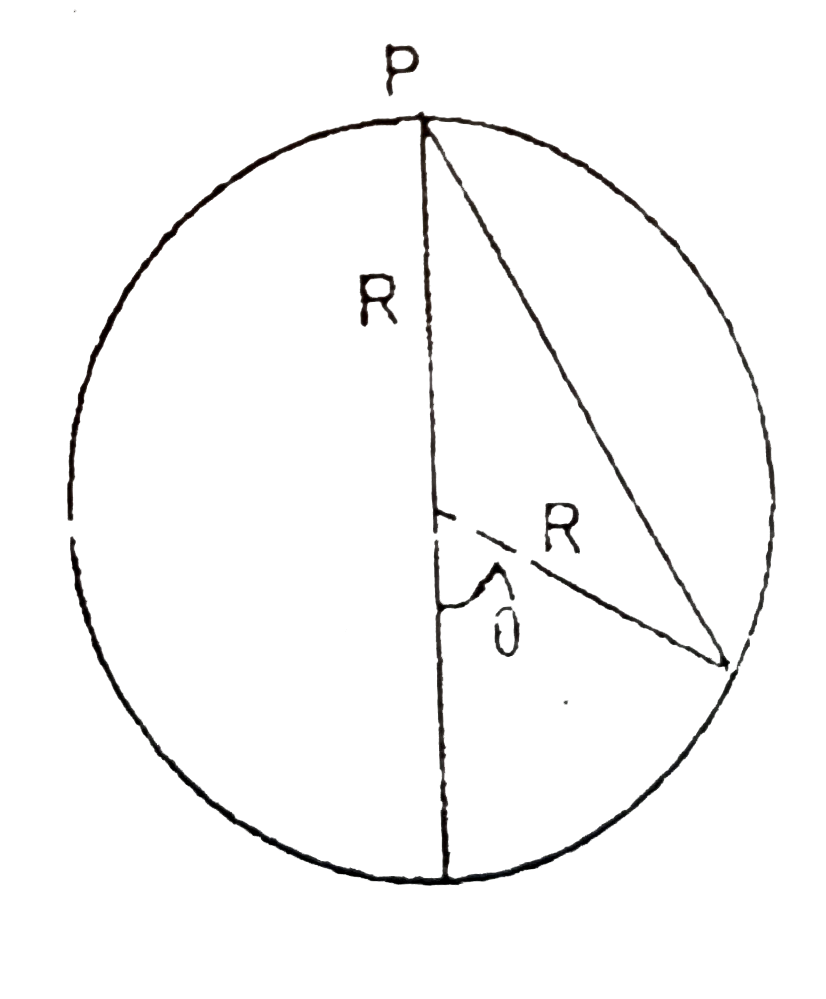
To reach $P$ in shortest time, $Q$ must be equal to $60^{\circ}$

The minimum time required to rach $P$ is $\frac{R}{v_{0}} [\frac{π}{6} + \sqrt{3}]$

The distance travelled to reach $P$ in shortest time is $R [\frac{π}{3} + \sqrt{3}]$ .

The angle $θ$ will not depend on the value of $v_{0}$ .

Video Solution

Text Solution

Verified by Experts

$T = \frac{R θ}{2 v_{0}} + \frac{2 R cos (θ / 2)}{v_{0}}$
$\frac{d T}{d θ} = 0 \Rightarrow \frac{R}{2 v_{0}} - \frac{R sin (θ / 2)}{v_{0}} = 0$
$\Rightarrow sin (θ / 2) = 1 / 2 \Rightarrow θ = 60^{\circ} \Rightarrow T = \frac{R}{v_{0}} [\frac{π}{6} + \sqrt{3}]$
Distance $= R \times \frac{π}{3} + 2 R \times \frac{\sqrt{3}}{2}$

Updated on:21/07/2023

For traffic moving at 60 km/hour along a circular track of radius 0.1 km, the correct angle of banking is
A ${{(60)}^{2} / 0.1}$ km
B ${tan}^{- 1} [\frac{{(50 / 3)}^{2}}{100 \times 9.8}]$
C ${tan}^{- 1} [\frac{100 \times 9.8}{{(50 / 3)}^{2}}]$
D ${tan}^{- 1} \sqrt{(60 \times 0.1 \times 9.8)}$