Consider a source of sound S, and an observer P. The source emits sound of frequency N0. The frequency observed by P is found to be N1 if P approaches S at a speed v and S is stationary; N2 if S approaches P at a speed v and P is stationary and N3 if each of P and S has speed v/2 towards one another
N1=N2=N3
N1<N2
N3<N0
N3 lies between N1 and N2
To solve the problem step by step, we will use the Doppler effect equations for sound, which describe how the frequency of sound changes for an observer moving relative to a source of sound.
Step 1: Understanding the Doppler Effect
The Doppler effect describes how the frequency of sound changes when the source or observer is moving. The formula for the observed frequency N when the source is stationary and the observer is moving towards the source is given by:
N=N0(v+vov)
Where:
- N0 is the emitted frequency of the source,
- v is the speed of sound,
- vo is the speed of the observer (positive if moving towards the source).
Step 2: Case 1 - Observer Approaching the Source
In this case, the observer P approaches the stationary source S with speed v. Here, vo=v and the speed of the source is 0. Therefore, we can write:
N1=N0(v+vv)=N0(2vv)=2N0
Step 3: Case 2 - Source Approaching the Observer
Now, the source S approaches the stationary observer P with speed v. In this case, the formula becomes:
N2=N0(vv−vs)
Where vs=v. Thus, we have:
N2=N0(vv−v)=N0(v0)
This indicates that N2 approaches infinity as the source approaches the observer at the speed of sound.
Step 4: Case 3 - Both Approaching Each Other
In this scenario, both the source S and observer P are moving towards each other with speed v/2. The observed frequency is given by:
N3=N0(v+v/2v−v/2)=N0(3v/2v/2)=N0⋅3
Step 5: Comparing Frequencies
Now we have:
- N1=2N0
- N2 approaches infinity
- N3=3N0
From this, we can conclude:
- N1<N3<N2
Conclusion
The correct options based on the observations are:
- N1<N3<N2
The Doppler effect describes how the frequency of sound changes when the source or observer is moving. The formula for the observed frequency N when the source is stationary and the observer is moving towards the source is given by:
- N0 is the emitted frequency of the source,
- v is the speed of sound,
- vo is the speed of the observer (positive if moving towards the source).
In this case, the observer P approaches the stationary source S with speed v. Here, vo=v and the speed of the source is 0. Therefore, we can write:
Now, the source S approaches the stationary observer P with speed v. In this case, the formula becomes:
In this scenario, both the source S and observer P are moving towards each other with speed v/2. The observed frequency is given by:
Now we have:
- N1=2N0
- N2 approaches infinity
- N3=3N0
- N1<N3<N2
The correct options based on the observations are:
- N1<N3<N2
Similar Questions
Consider a souce of sound S, and an observer/detector D. The source emits a sound wave of frequency f0. The frequency observed by D is found to be (i) f1, if D approaches S and S is stationary
(ii) f2, if S approaches S and S is stationary
(iii) f3,if both S and D and D is stationary Speed
In all three cases, relative velocity of S wrt D is the same. For this situation which is incorrect?View Solutiona bus is moving towards and stationary observer with speed 20 m/s blows a horn of frequency 200 Hz. the frequency of sound heard by the observer is approximately ( take speed of sound 320 m/s)
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more that the actual frequency. If the speed of sound is v, that of the source is
View Solution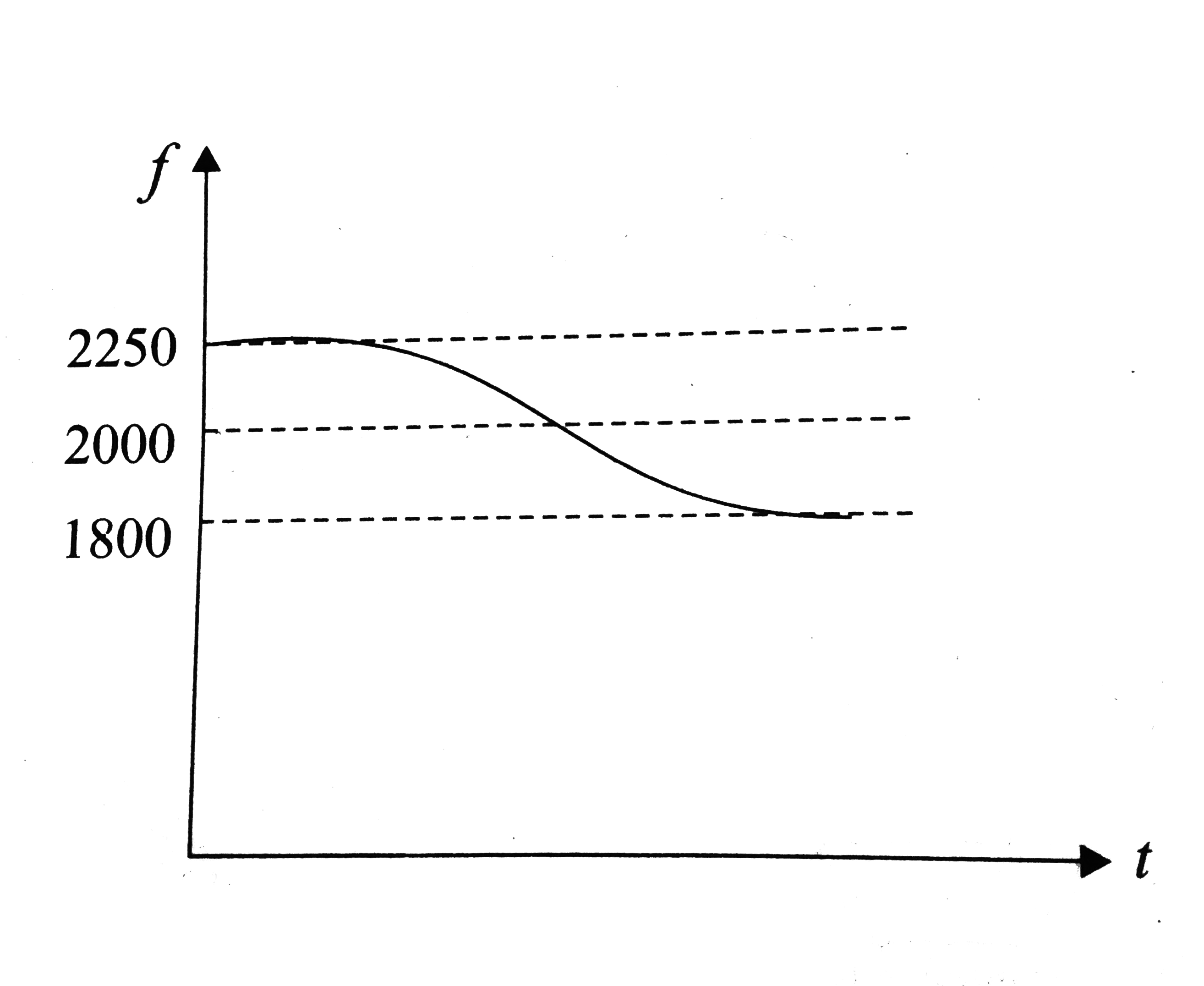
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300msView Solutionwhen a source of sound of frequency f crosses stationary observer with a speed vs(<< speed of sound v) , the apparent change in frequency Δf is given by
View SolutionA source of sound and an observer are approaching each other with the same speed, which is equal to (110) times the speed of sound. The apparent relative change in frequency of source is
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View Solutionwhen a source is going away from a stationary observer with the velocity equal to that of sound in air , then the frequency heard by observer is n times the original frequency . The value of n is
View SolutionWhen a source moves away from a stationary observer, the frequency is 67 times the original frequency. Given: speed of sound =330ms . The speed of the source is
View SolutionA source is moving towards an observer with a speed of 20 m / s and having frequency of 240 Hz . The observer is now moving towards the source with a speed of 20 m / s . Apparent frequency heard by observer, if velocity of sound is 340 m / s , is
View Solution

