A solid transparent sphere made of glass (R.I.=μ>1) has a small, opaque dot at its centre. When observed from outside, apparent position of dot will be
closer to eye than its actual position
farther from eye than its actual position
same as its actual position
independent of refractive index of the sphere
To solve the problem of determining the apparent position of a small opaque dot at the center of a solid transparent sphere made of glass (with a refractive index greater than 1), we can follow these steps:
1. Understand the Setup:
- We have a solid transparent sphere made of glass with a refractive index μ (where μ>1).
- There is a small opaque dot at the center of the sphere.
- We need to find the apparent position of this dot when observed from outside the sphere.
2. Identify the Relevant Formula:
- We will use the lens maker's formula, which relates the object distance U, the image distance V, and the refractive indices of the two media involved:
μ2V−μ1U=μ2−μ1R
where:
- μ2 is the refractive index of the glass sphere (which is μ),
- μ1 is the refractive index of air (approximately 1),
- R is the radius of curvature of the sphere.
3. Assign Values:
- For the dot at the center of the sphere, the object distance U is taken as negative since it is on the same side as the incoming light (inside the sphere). Thus, U=−R.
- The radius of curvature R is positive for a convex surface.
4. Substitute Values into the Formula:
- Substitute μ2=μ, μ1=1, and U=−R into the lens maker's formula:
μV−1−R=μ−1R
5. Simplify the Equation:
- Rearranging gives:
μV+1R=μ−1R
- This can be rewritten as:
μV=μ−1−1R=μ−2R
6. Solve for V:
- Cross-multiplying gives:
μR=V(μ−2)
- Thus, we find:
V=μRμ−2
7. Interpret the Result:
- Since μ>1, μ−2 will be negative, indicating that V is negative. This means the image is formed on the same side as the object (the left side in our diagram).
- The negative sign indicates that the apparent position of the dot is at a distance of −R from the center, which means it appears to be at its actual position.
Conclusion:
The apparent position of the dot, when observed from outside the sphere, is the same as its actual position.
- We have a solid transparent sphere made of glass with a refractive index μ (where μ>1).
- There is a small opaque dot at the center of the sphere.
- We need to find the apparent position of this dot when observed from outside the sphere.
- We will use the lens maker's formula, which relates the object distance U, the image distance V, and the refractive indices of the two media involved:
μ2V−μ1U=μ2−μ1R
where:
- μ2 is the refractive index of the glass sphere (which is μ),
- μ1 is the refractive index of air (approximately 1),
- R is the radius of curvature of the sphere.
- For the dot at the center of the sphere, the object distance U is taken as negative since it is on the same side as the incoming light (inside the sphere). Thus, U=−R.
- The radius of curvature R is positive for a convex surface.
- Substitute μ2=μ, μ1=1, and U=−R into the lens maker's formula:
μV−1−R=μ−1R
- Rearranging gives:
μV+1R=μ−1R
- This can be rewritten as:
μV=μ−1−1R=μ−2R
- Cross-multiplying gives:
μR=V(μ−2)
- Thus, we find:
V=μRμ−2
- Since μ>1, μ−2 will be negative, indicating that V is negative. This means the image is formed on the same side as the object (the left side in our diagram).
- The negative sign indicates that the apparent position of the dot is at a distance of −R from the center, which means it appears to be at its actual position.
The apparent position of the dot, when observed from outside the sphere, is the same as its actual position.
Similar Questions
A glass sphere (μ=1.5) of radius 20 cm has a small air bubble 4 cm below its centre. The sphere is viewed from outside and along a vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
View SolutionDoes the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?
View SolutionA sphere (μ=43) of radius 1m has a small cavity of diameter 1cm at its centre. An observer who is looking at it from tight, sees the magnification of diameter of the cavity as
View SolutionA small air bubble in a sphere of glass with radius 4 cm appears to be 1 cm from the surface when observed along a diameter. Find the true positino of the air bubble.
View SolutionA hollow sphere of glass of R.I .n has small mark M on its interior surface which is observed by an observer O from a point outside the sphere, .C is centre of the sphere. The inner cavity (air) is concentric with the external surface and thickness of the glass is every where equal to the radius of the inner surface. Find the distance by which the mark will appear nearer than it really is in terms of n and R assuming paraxial rays.
_E01_156_Q01.png)
View SolutionIn a spherical paper weight (R = 10 cm) made of glass of refractive index μ=32, an object is embedded at a distance 5 cm from its centre. What is the apparent position of the object when seen from the opposite side (see figure)?
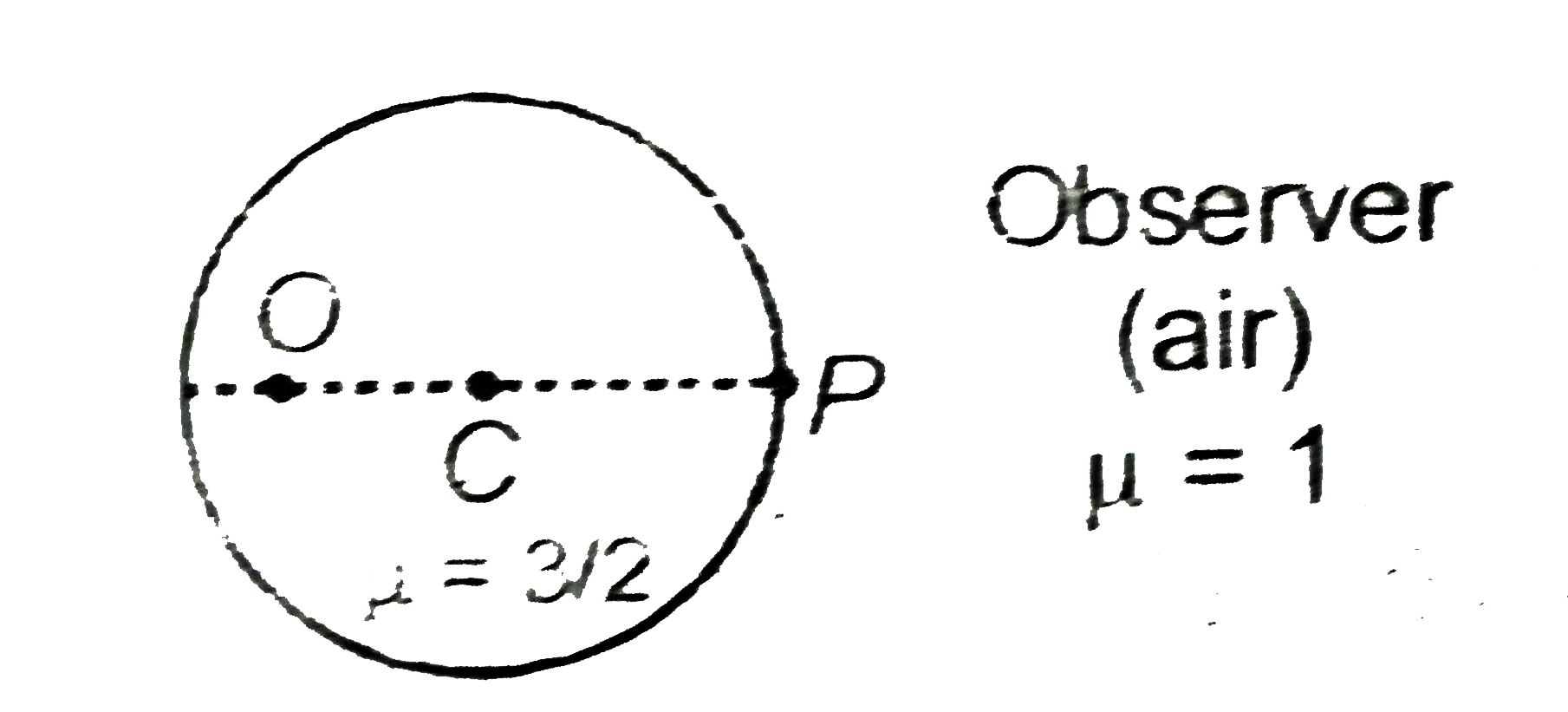
View SolutionA glass sphere of radius 5 cm has a small bubble at a distance 2 cm from its centre.The bubble is viewed along a Diameter of the sphere from the side on which it lies.How far from the surface will it appear.Refractive index of glass is 1.5
2.5 cm behind the surface
View SolutionA transparent glass sphere of radius 10 cm and refractive index μ=1.5 has its one half silvered so that it acts like a concave mirror. Find the position of final image for an object O at (a) 30 cm to the left of the front surface of the ball.

View SolutionA hollow sphere of glass of inner and outer radii R and 2R respectively has a small mark on its inner surface. This mark is observed from a point outside the sphere such that the centre of the sphere lies in between. Prove that the mark will appear nearer than it really it, by a distance (μ−1)(R)/(3μ−1)
View SolutionA sphere made of transparent material of refractive index (μ=32 )and of radius 50 cm has a small air bubble 10 cm below the surface. The apparent depth of the bubble if viewed from outside normally is
View Solution
