Shown in the diagram is a system of two bodies, a block of mas m and a disc of mass M, held in equilibrium. If the string 3 is burnt, find the acceleration of the disc. Neglect the masses of the pulleys P and Q. (The coefficient of friction between the block and horizontal surface is μ)

Referring to the free-body diagram we write the equation of motion.
For the block m :
T1−μN=ma1……(1)
and N−mg=0…(2)
For pulley P :
mpg+T2−2T1=mpap
Since the pulley is light,
∴mp≈0
⇒T2=2T1.....(3)
For disc M.
Mg−2T2=Ma2......(4)
From the geometry of the figure the positions of the parts m, P and M are related as x1+2y1=l1 and (y2−y1)+y2=l2, where l1 and l2 are the lengths of the strings 1 and 2, respectively. Eliminating y1 from these two equations, we obtain,
x1+4y2=l1+2l2 ,
Differntiating both sides twice w.r.t. time, we obtain d2x1dt2+4d1y2dt2=0
⇒a1=4a2.....(5)
From Eqs. (1) and (2), we get
T1−μmg=ma1.......(6)
From Eqs. (3) and (4), we get
Mg−4T1=Ma2.....(7)
Eliminating T1 from Eqs. (6) and (7) and putting a1=4a2, we obtain
a2=M−4μmM+16mg.

Topper's Solved these Questions
Similar Questions
Determine the acceleration of the 5kg block A . Neglect the mass of the pulley and cords . The block B has a mass of 10kg, The coefficient of kinetic friction between block B and the surface is μk=0.1 (take g=10m/s2)

View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
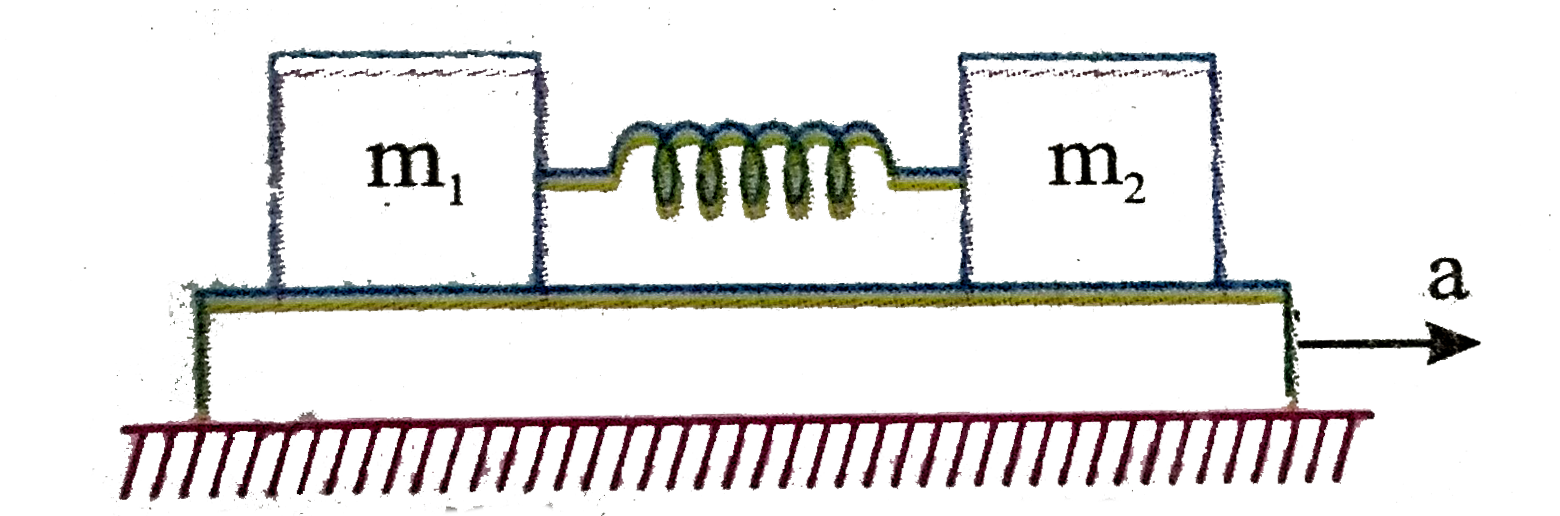
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
View SolutionIn the figure shown a ring of mass M and a block of mass m are in equilibrium. The string is light and pulley P does not offer any friction and coefficient of friction between pole and M is μ. The frictional force offered by the pole to M is

View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.

View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionTwo block of masses M and m are connected to each other by a massless string and spring of force constant k as shown in the figure. The spring passes over a frictionless pulley connected rigidly to the egde of a stationary block A. The coefficient of friction between block M and plane horizontal surface of A is μ. The block M slides over the horizontal top surface of A and block m slides vertically downward with the same speed. The mass M is equal to

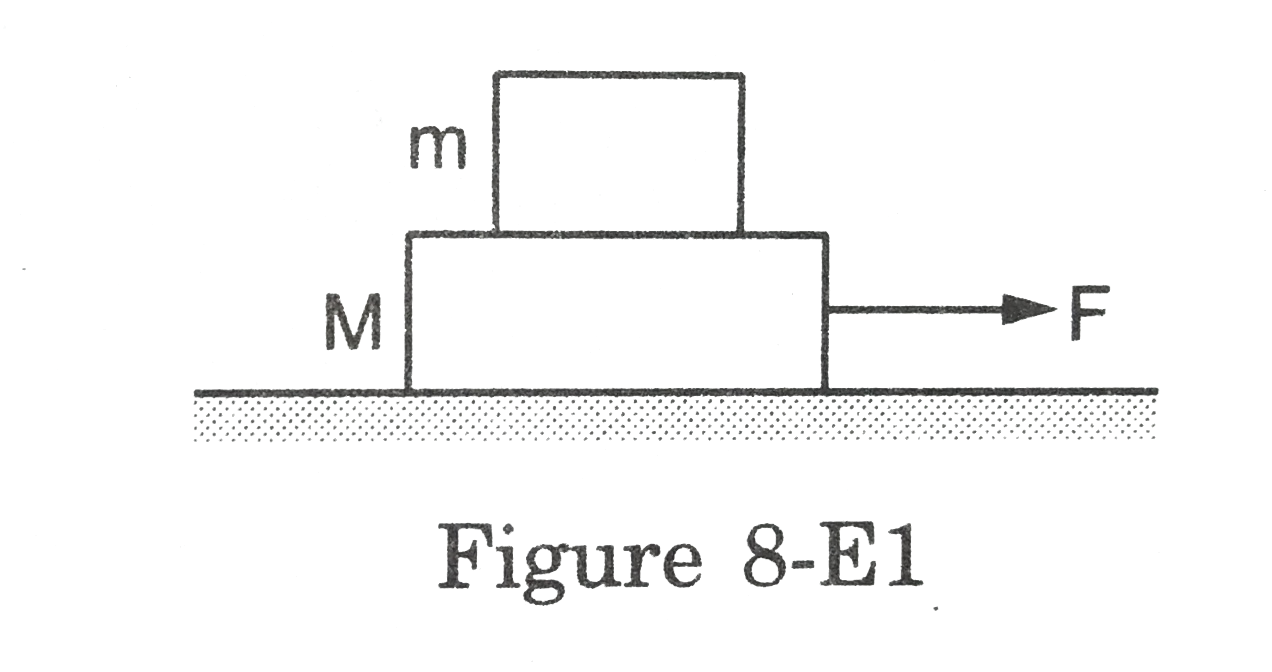
View SolutionA block of mass m is kept over another block of mass M nd the system rests on a horizontal force F acting on the lower block produces an accelertion F2(m+M) in the system the two blocks always move together. A. Find the coefficient of kinetic frictioin between the bigger block and th horizontal surface. b. find the frictional force acting on the smaller block. c. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
View Solution
