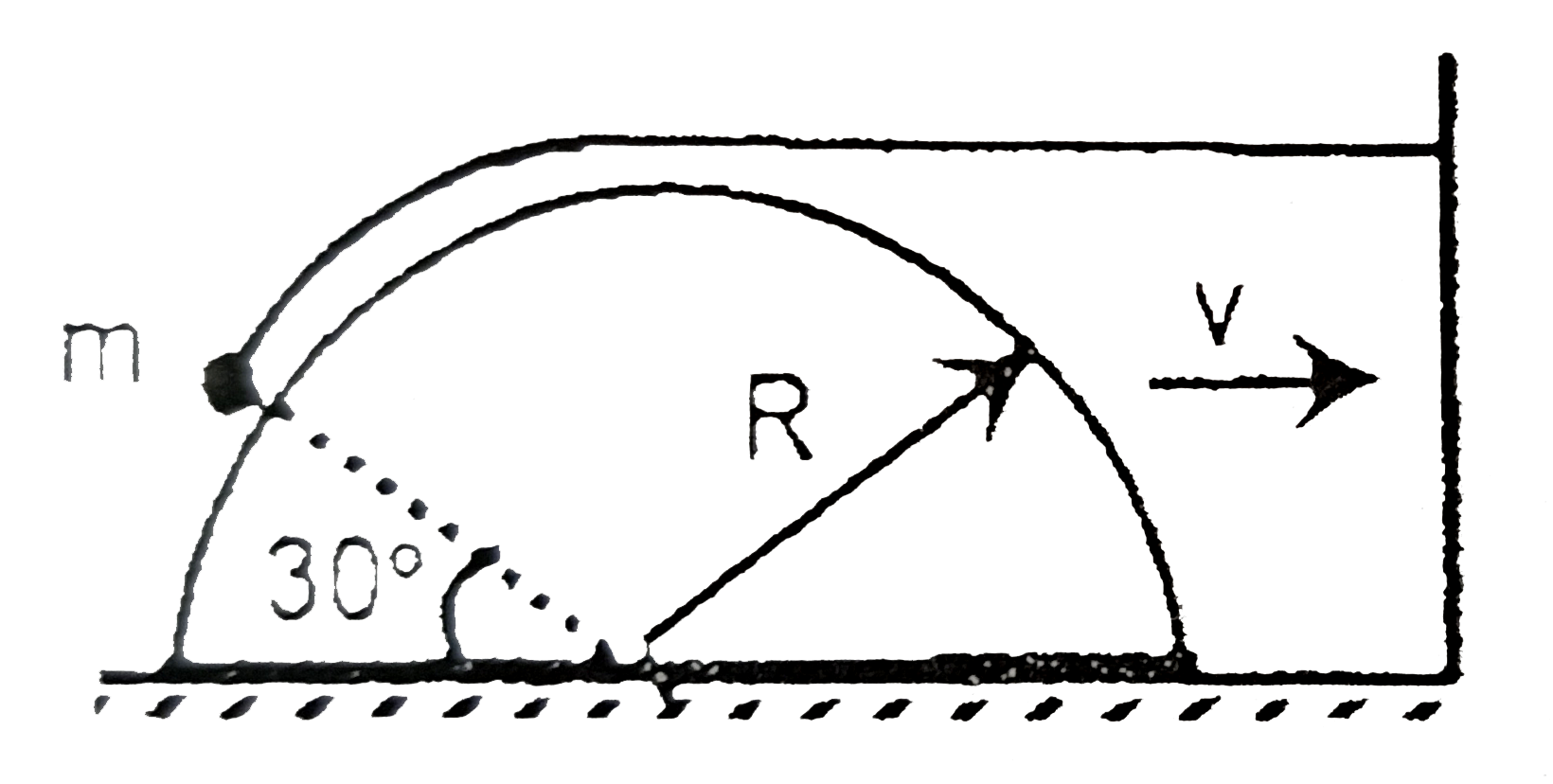
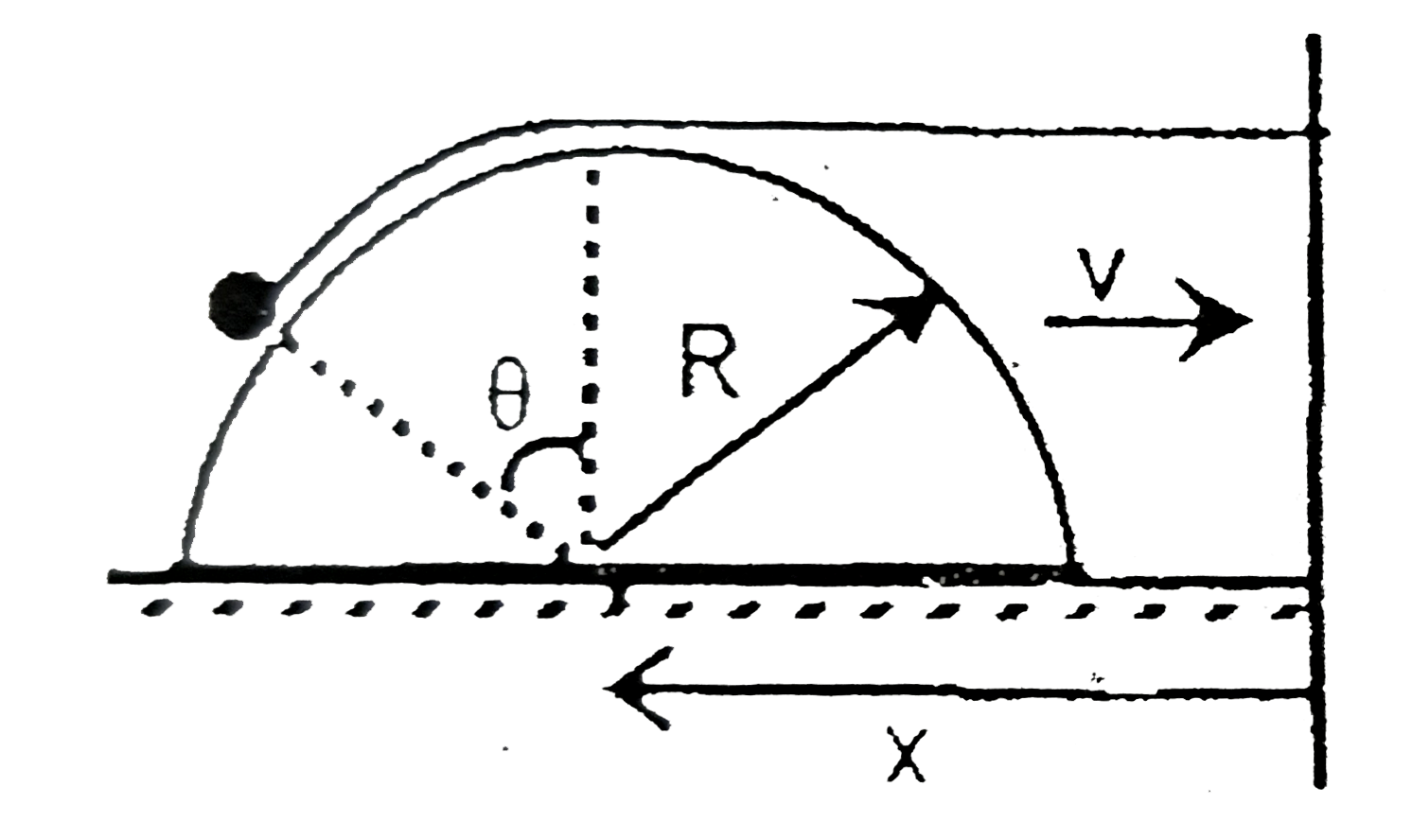
A point objects of mass m is slipping down on a smooth hemispherical body of mass M and radius R. The point object is tied to a wall with an ideal string as shown. At a certain instant, speed of the hemisphere is v and its acceleration is a. Then speed vp and acceleration ap of a particle has value (Assume all the surfaces in contact are frictionless)
vP=vsin60∘
vP=v
aP=a
aP= ⎷[(v2R)+(a√32)]2+(a2)2
x+Rθ= constant
dxdt+Rdθdt=0
∴ω=dθdt=vR
α=dω/dt=a/R
At θ=60∘,
∴vP=v and aP=
⎷(a√32+v2R)+(a2)2
Topper's Solved these Questions
Similar Questions
A point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
 View Solution
View SolutionA particle of mass 'm' is moving along a circle of radius 'r'. At some instant, its speed is 'v' and it is gaining speed at a uniform rate'a', then, at the given instant, acceleration of the particle is :
View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.
 View Solution
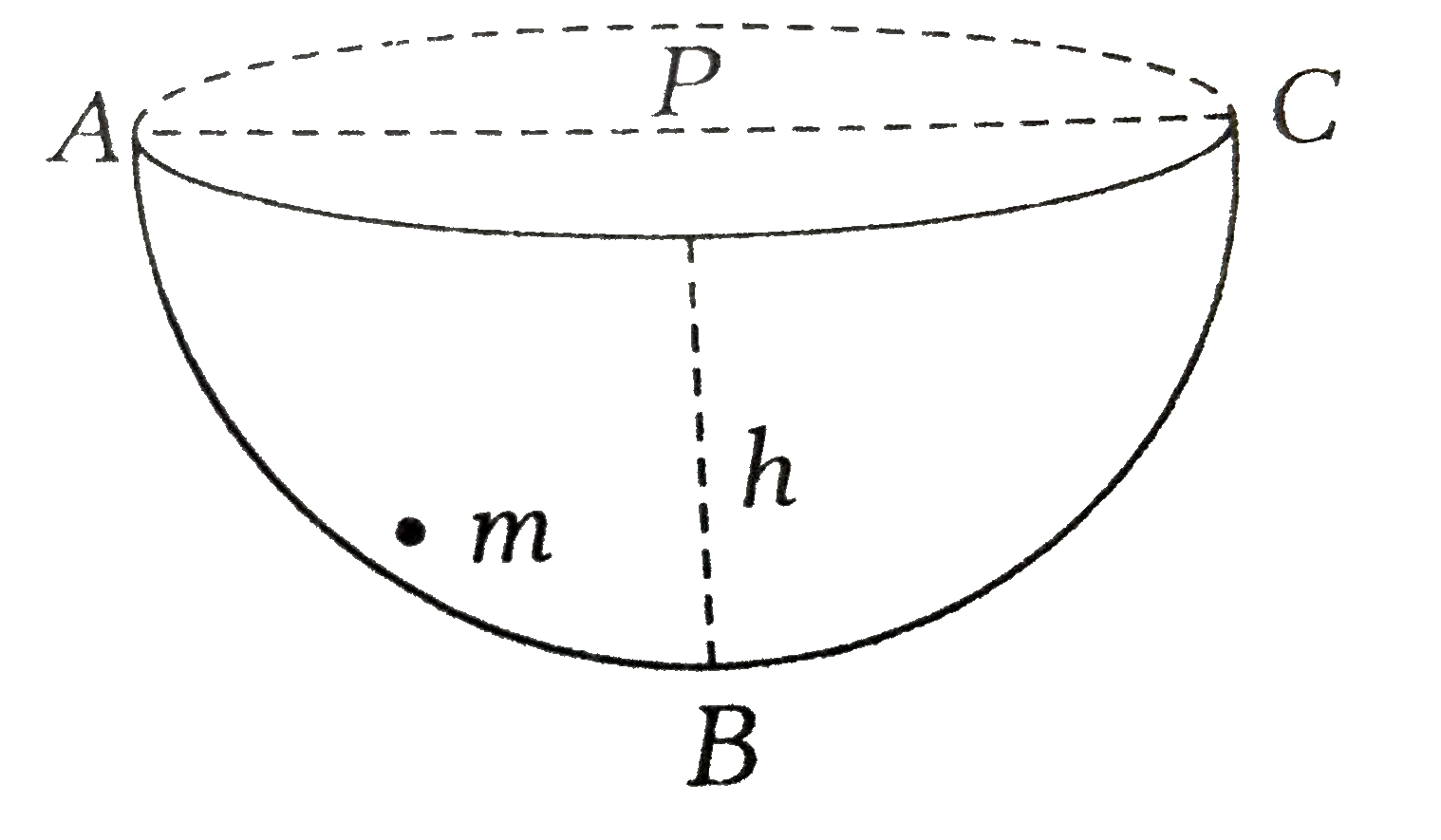
View SolutionA particle of mass m makes SHM in a smooth hemispherical bowl ABC and it moves from A to C and back to A via ABC,so that PB=h. Find the speed of the ball when it just crosses the point B.
 View Solution
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .View Solution
.View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .View Solution
.View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View SolutionA Particle of mass 'M' moves in a uniform circular path of radius 'r' with a constant speed 'v' then its centripetal acceleration is .
View SolutionA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 View Solution
View Solution

