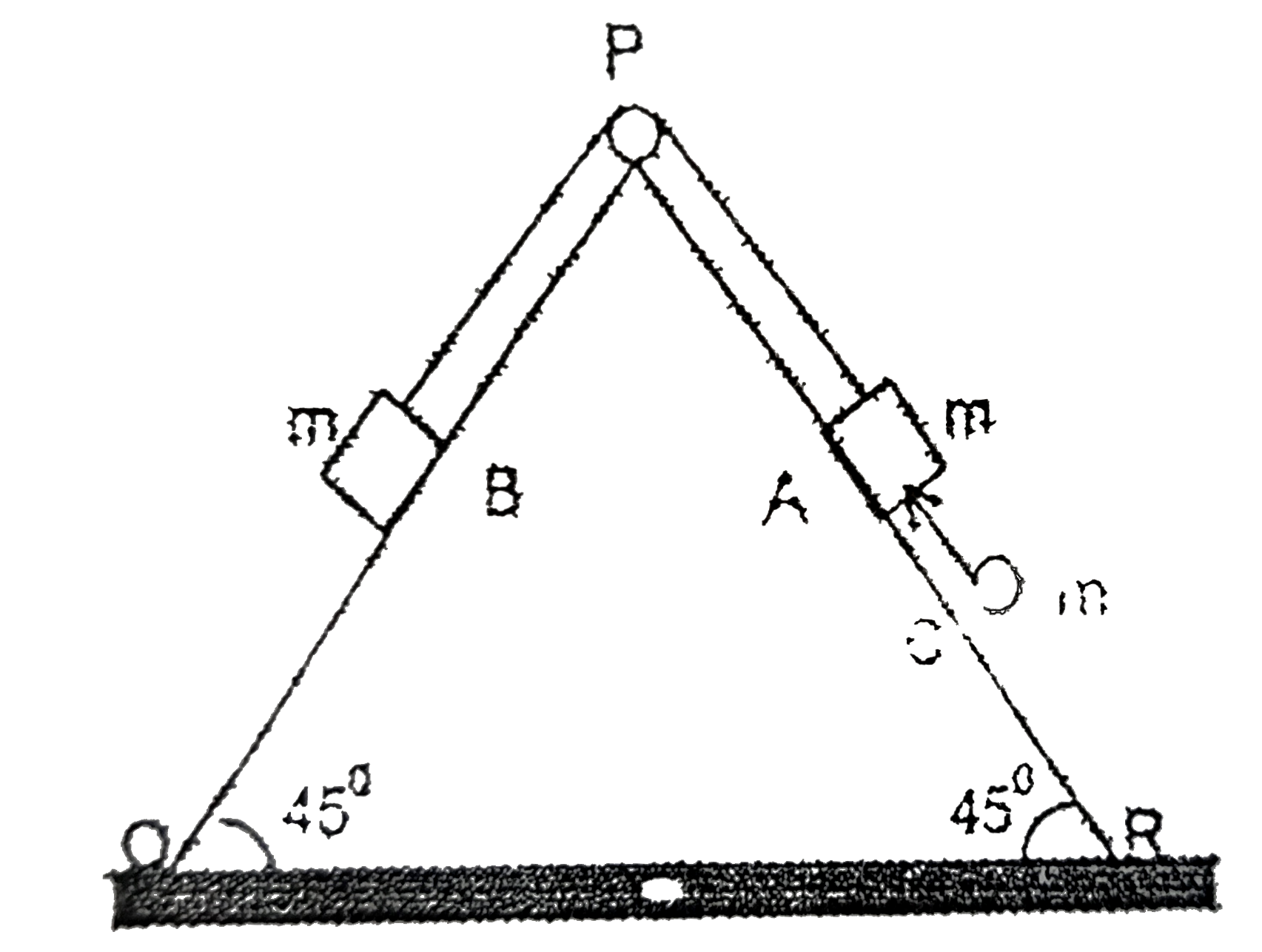
PQR is a wedge fixed to the floor. Two blocks A & B of equal mass m=1kg is placed on either side of wedge connected through a string passing over the pulley P. Initially PB=PA. Another block C of mass m=1kg moving with a velocity 10m/s collides inelasically with A. All the surfaces are smooth and pulley & string are massless.
(a) What should be the minimum length of the string AB so that block A does not hit the pulley ?
(b) What is the loss in meechanical energy from the instant C hits A to the instant when B starts moving upward ? (g=10m/s2)
(a) Conservation of momentum,
mcvc=(mA+mC)×v1, v1= common velocity of (A+C) mass.
∴V1=mcvcmA+mC=1×102=5m/s.
String slacks and B starts moving downward under acc=gsin45∘.
∴(A+C) moves under retardation of gsin45∘ and come to rest after time
5=10×1√2t⇒t=0.707sec.
Distance moved in this time
S1=v212gsin45∘=5×5×√22×10=54√2=1.76m.
Now, string will again become taut and (A+C) will experience a jerk.
Velocity of B at this time =5m/s
∴ Conservation of momentum
for B:1×5−J=1×v2, J=impulse generated
for (A+C):J=2×v2, v2= common velocity of (A+C) after string has become taut
∴v2=53m/s
Now (A+C) will start moving upward with v2 velocity under retardation
a=(m(A+C)−mBmA+C+mB)gsin45∘=(2−13)×10×1√2=103√2m/s2
∴(A+C) will come to rest after moving distance
S2=(5/3)×(5/3)2×(10/3√2)=56√2m=0.59m
∴ Net length risen by (A+C)=S1+S2=2.35m.
∴ Length of the string must be at least l=2×2.35=4.7m
(b) Energy loss in collision =12mCv2c−12(mA+mC)v21
=12×1×100−12×2×25=25J
Loss in impulsive jerk
=12mBv21−12(ma+mA+mc)v22=12×1×25−12×3×259
=252[1−13]=253J
∴ Net loss =25+253=4×253=1003=33.33J
Topper's Solved these Questions
Similar Questions
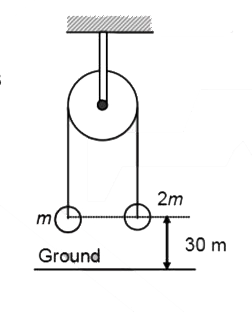
Two masses m and 2m are connected by a massless string, which passes over a pulley as shown in figure. The masses are held initially with equal lengths of the strings on either side of the pulley. Find the velocity of masses at the instant the lighter mass moves up a distance of 15m. ( g=10m/s2 )
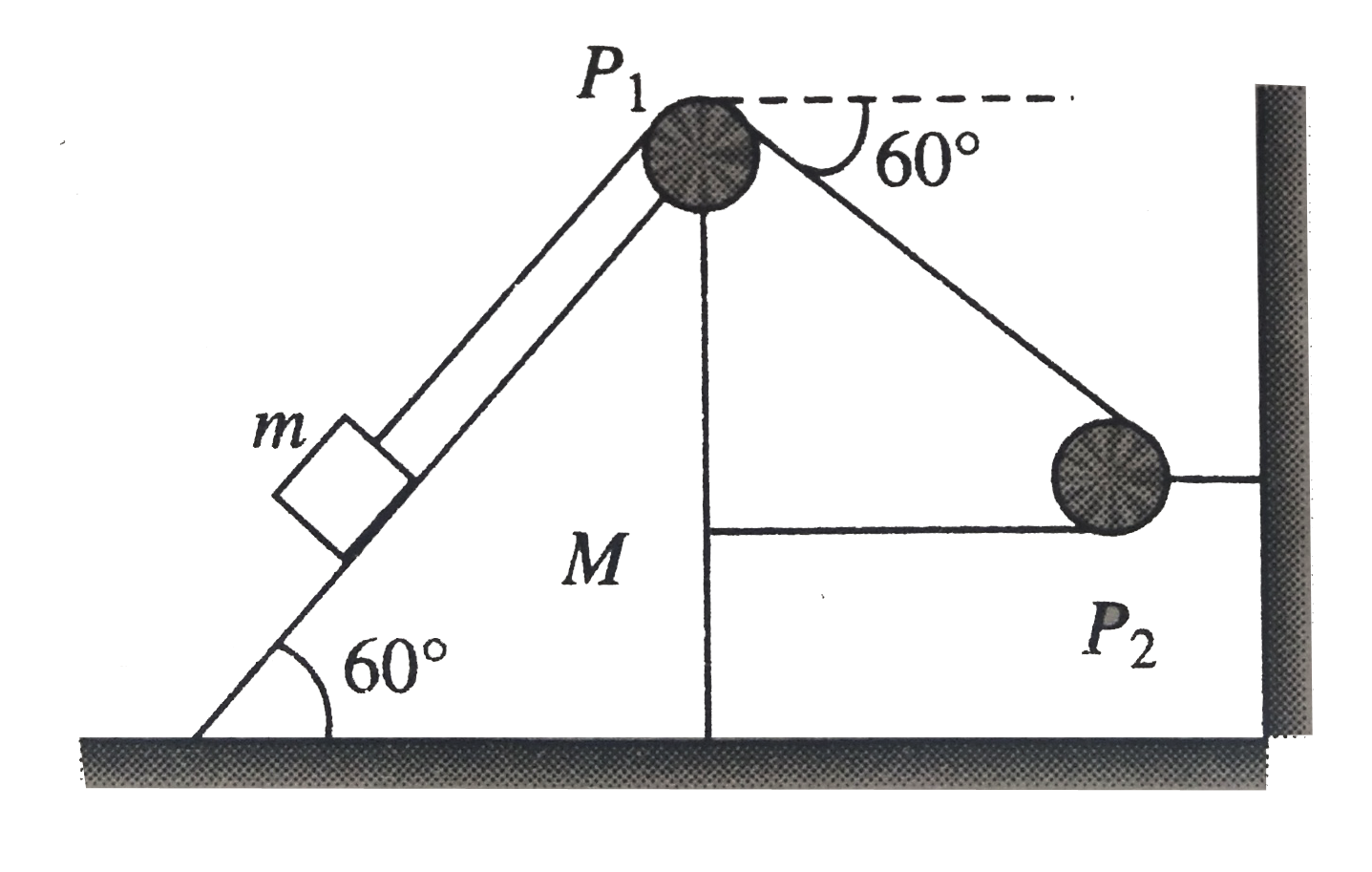
View SolutionIn the arrangement shown in fig. the block of mass m=2kg lies on the wedge of mass M=8kg. The initial acceleration of the wedge, if the surfaces are smooth, is
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionFigure shows an arrangement of pulleys and two blocks. All surfaces are frictionless . All pulleys and strings are massless. All string are smooth and massless.
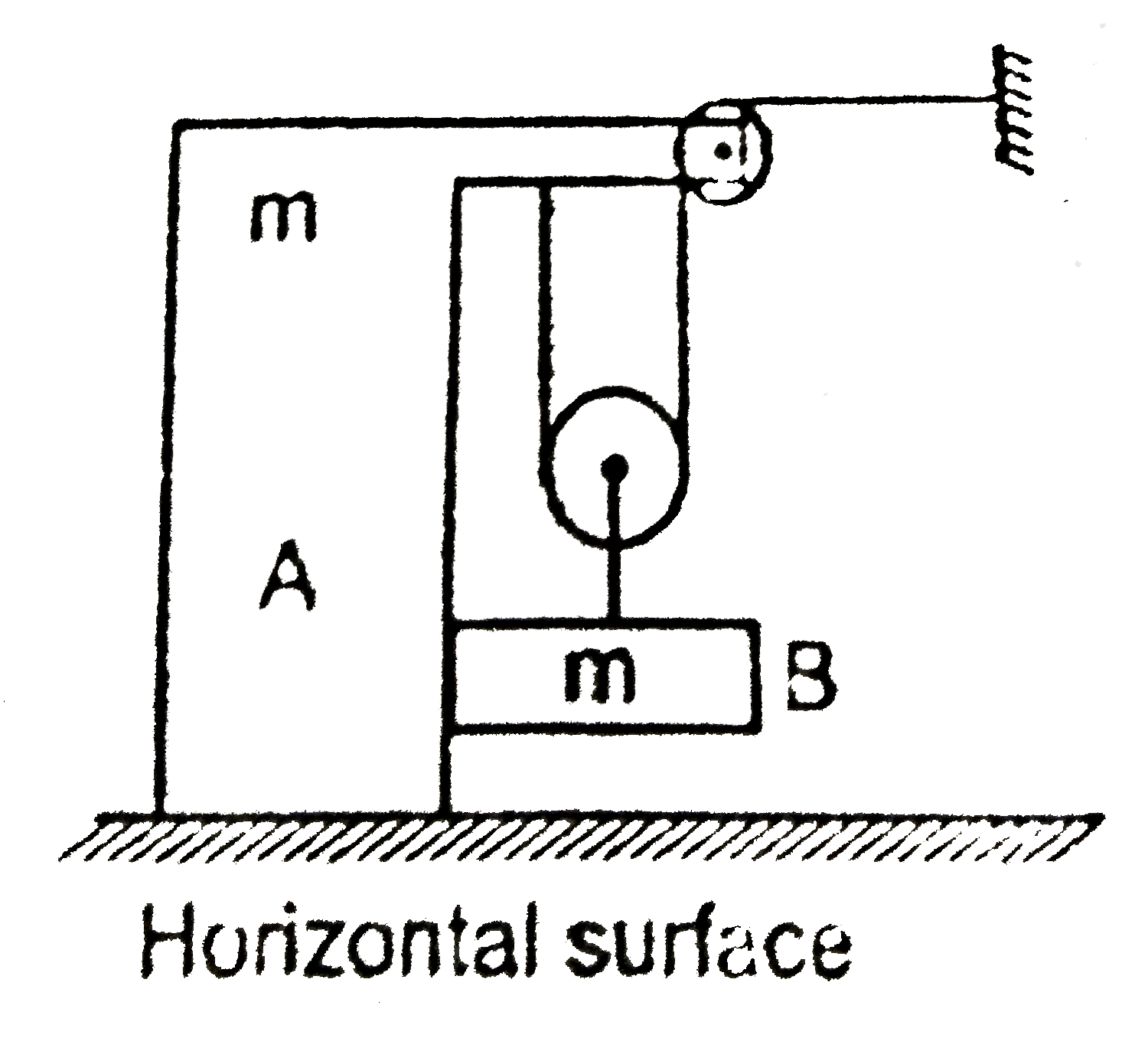
The acceleration of block A is :
View SolutionIn the arrangement shown in fig. the block of mass m=2kg lies on the wedge of mass M=8kg. The initial acceleration of the wedge, if the surfaces are smooth, is

View SolutionFigure shows an arrangement of pulleys and two blocks. All surfaces are frictionless . All pulleys and strings are massless. All string are smooth and massless.

The acceleration of block A is :
View Solution
