A particle of mass m is released from height ‘h’ on smooth quarter circular fixed wedge. The horizontal surface AB following the circular path at bottom of wedge is rough with coefficient of friction μ between surface and m. Find the distance from A where the mass will stop.
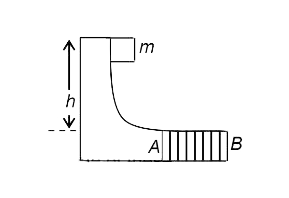
2hμ
hμ
hμg
none of these
By work energy theorem,
mgh−μmgs=0
⇒s=hμ
Topper's Solved these Questions
Similar Questions
A particle of mass m is released from height h on smooth quarter circular fixed wedge. The horizontal surface AB following the circular path at bottom of wedge is rough with coefficient of friction μ between surface and m. Find the distance from bottom of wedge where the mass will stop.

View SolutionA body of mass m is released from a height h on a smooth inclined plane that is shown in the figure. The following can be true about the velocity of the block knowing that the wedge is fixed.
 .
.
View SolutionA body of mass m is released from a height h on a smooth inclined plane that is shown in the figure. The following can be true about the velocity of the block knowing that the wedge is fixed.
 .
.
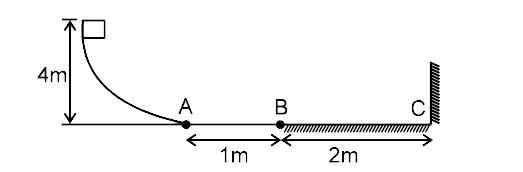
View SolutionA block of mass m = 0.1 kg is released from a height of 4m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction μ = 01. If the impact of block with the vertical wall at C be elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take g=10m/s2)

View SolutionA block of mass m = 0.1 kg is released from a height of 4 m on a curved smooth surface. On the horizontal surface, path AB is smooth and path BC offers coefficient of friction μ=0.1. If the impact of block with the vertical wall at C be perfectely elastic, the total distance covered by the block on the horizontal surface before coming to rest will be (take g=10ms–2) -
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

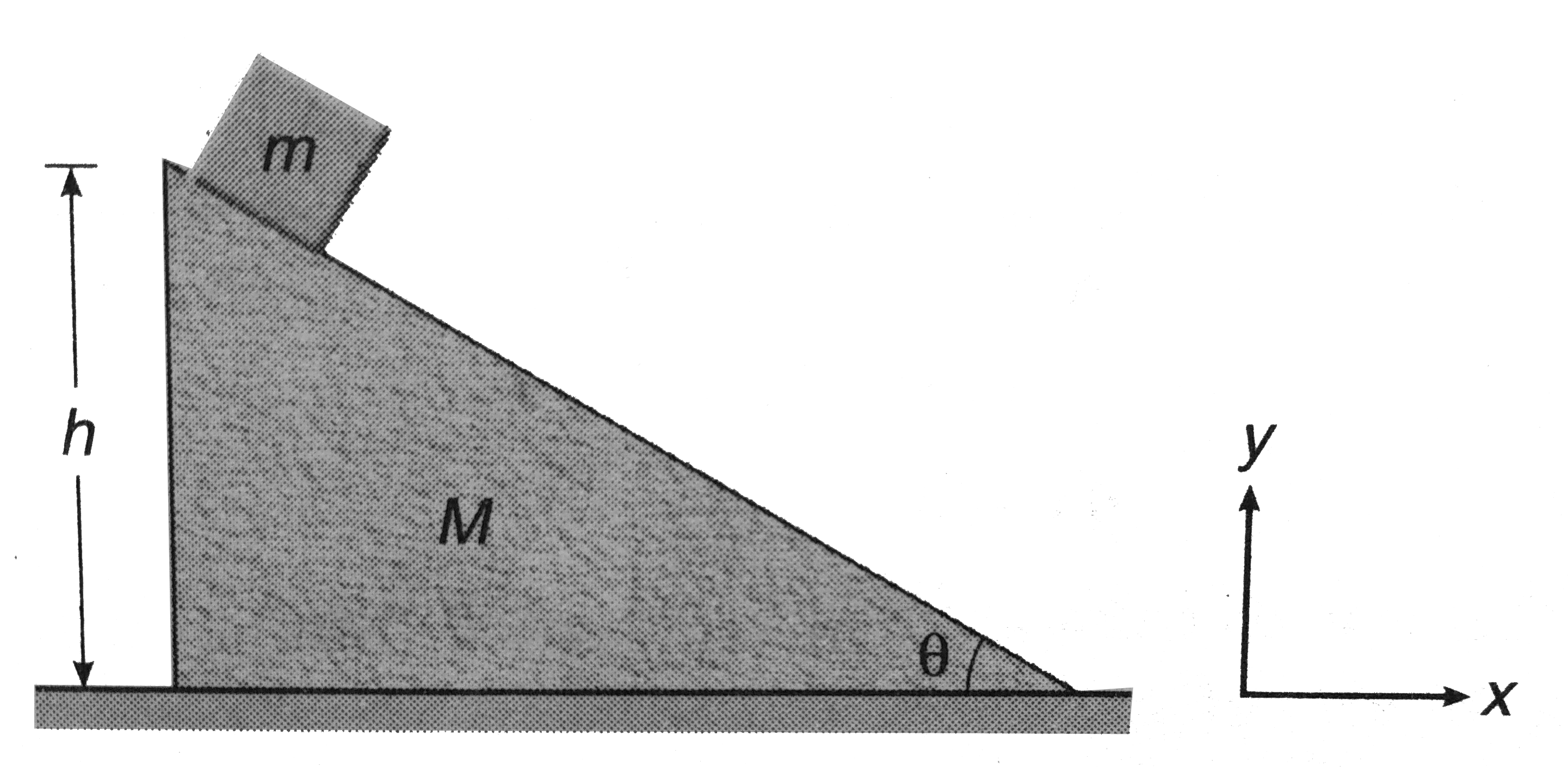
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View Solution
