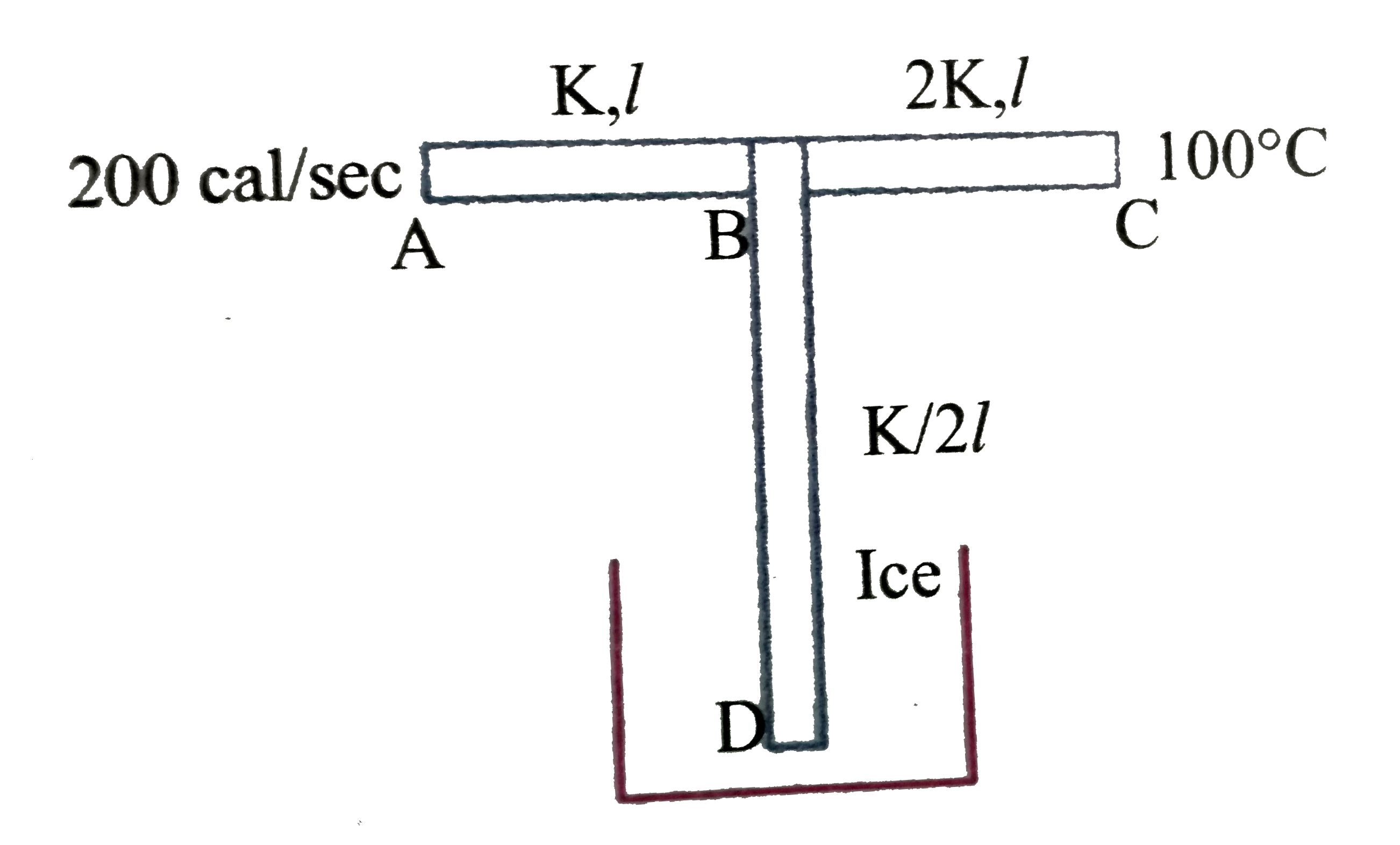
Three rods AB,BC and BD of same length l and cross-sectionsl area A are arranged as shown . The end D is immersed in ice whose mass is 440gm Heat is being supplied at constant rate of 200cal/sec from the end Time in which whole ice will melt (Latent heat of fusion of ice is 80cal/gm
 .
.
403min
700sec
20/3min
indefinitely long time
If θ be temperature of B, then
2kA(θ−100)l+(k/2)A(θ−0)l=200
Substituting value θ=880∘C
∴Φ1=mL
kA(880−0)2l×t=440×80
t=80×1×2×440100×10×10−4×880=800sec=(40/3)min
Topper's Solved these Questions
Similar Questions
Three rods AB,BC and BD of same length l and cross sectional area A are arranged as shown. The end D is immersed in ice whose mass is 440 gm. Heat is being supplied at constant rate of 200 cal /sec from the end A. Find out time (in sec) in which wholeice will melt. (latent heat of fusion of ice is 80 cal/gm)
Given k (thermal conductivity) =100 cal/m/sec/∘C,A=10cm2,l=1m
View Solution
Three rods AB, BC and BD of same length l and cross section A are arranged as shown. The end D is immersed in ice whose mass is 440 g and is at 0∘C. The end C is maintained at 100∘C. Heat is supplied at constant rate of 200 cal/s. Thermal conductivities of AB, BC and BD are K, 2K and K/2, respectively Time after which whole ice will melt is (K=100cal/m−s∘CA=10cm2,l=1cm)
View Solution
Three rods AB, BC and BD of same length l and cross section A are arranged as shown. The end D is immersed in ice whose mass is 440 g and is at 0∘C. The end C is maintained at 100∘C. Heat is supplied at constant rate of 200 cal/s. Thermal conductivities of AB, BC and BD are K, 2K and K/2, respectively Time after which whole ice will melt is (K=100cal/m−s∘CA=10cm2,l=1cm)
View SolutionA coil of water of resistance 50Ω is embedded in a block of ice and a potential difference of 210 V is applied across it. The amount of ice which melts in 1 second is [ latent heat of fusion of ice =80calg−1]
View SolutionTwo rods A and B of same area of cross-section are joined together end to end The free end of the rod A is kept in melting ice at 300 K and free end of B rod at 400 K. The rods are of the same length. The conductivity of A is 3 times that of B. Calculate the temperature of the junction of the rods.
View SolutionOne end of a brass rod of length 2.0 m and cross section 1cm2 is kept in steam at 100∘C and the other end in ice at 0∘C. The lateral surface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is 110W/m−K and specific latent heat of fusion of ice is 80cal/g.
View SolutionHeat is being supplied at a constant rate to the sphere of ice which is melting at the rate of 0.1 gm/s. It melts completely in 100 s. The rate of rise of temperature thereafter will be
View SolutionFive rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.
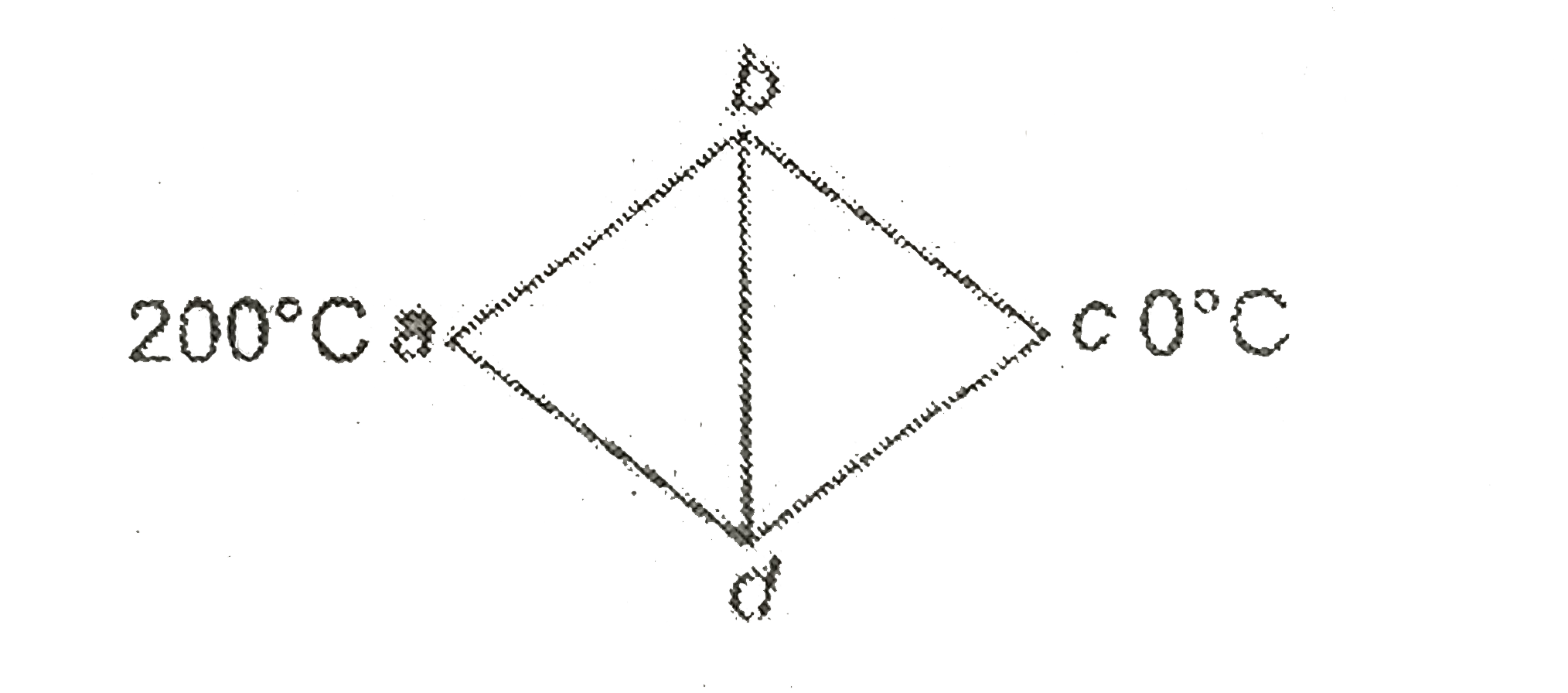
For what length x of rod dc there will be no heat flow through rod bd ?
View SolutionThree rods AB, BC and AC having thermal resistances of 10 units, 10 units and 20 units, respectively, are connected as shown in the figure. Ends A and C are maintained at constant temperatures of 100∘C and 0∘C, respectively. The rate at which the heat is crossing junction B is

View Solution2kg ice at −20∘C is mixed with 5kg water at 20∘C. Then final amount of water in the mixture will be: [specific heat of ice =0.5cal/gm∘C, Specific heat of water =1cal/gm∘C, Latent heat of fusion of ice =80cal/gm]
View Solution
