In the illustration 1 if the particle shifts from Points P to points C find the displacement of the particle.
To find the displacement of the particle as it shifts from point P to point C, we will follow these steps:
Step 1: Identify the coordinates of points P and C
- From the given information, we can determine the coordinates of the points:
- Point P is located at (2.5, 2) meters.
- Point C is located at (0, 4) meters.
Step 2: Write the position vectors for points P and C
- The position vector for point P (OP) can be expressed as:
→OP=2.5^i+2^j meters
- The position vector for point C (OC) can be expressed as:
→OC=0^i+4^j meters
Step 3: Calculate the displacement vector
- The displacement vector (→d) from point P to point C is given by:
→d=→OC−→OP
- Substituting the position vectors:
→d=(0^i+4^j)−(2.5^i+2^j)
- This simplifies to:
→d=(0−2.5)^i+(4−2)^j
→d=−2.5^i+2^j meters
Step 4: State the final displacement
- The displacement of the particle from point P to point C is:
→d=−2.5^i+2^j meters
Summary
The displacement of the particle as it shifts from point P to point C is −2.5^i+2^j meters.
---
- From the given information, we can determine the coordinates of the points:
- Point P is located at (2.5, 2) meters.
- Point C is located at (0, 4) meters.
- The position vector for point P (OP) can be expressed as:
→OP=2.5^i+2^j meters
- The position vector for point C (OC) can be expressed as:
→OC=0^i+4^j meters
- The displacement vector (→d) from point P to point C is given by:
→d=→OC−→OP
- Substituting the position vectors:
→d=(0^i+4^j)−(2.5^i+2^j)
- This simplifies to:
→d=(0−2.5)^i+(4−2)^j
→d=−2.5^i+2^j meters
- The displacement of the particle from point P to point C is:
→d=−2.5^i+2^j meters
The displacement of the particle as it shifts from point P to point C is −2.5^i+2^j meters.
Similar Questions
A particle travels from A to B path shown in figure, then the displacement of particle is :
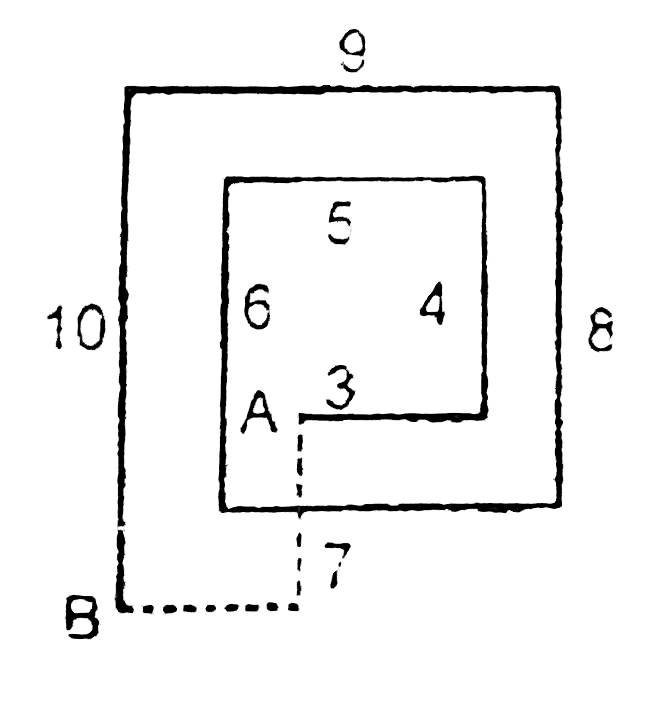 .View Solution
.View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.View Solutionvelocity time graph of a particle is shown in figure. Find displacement of the particle.
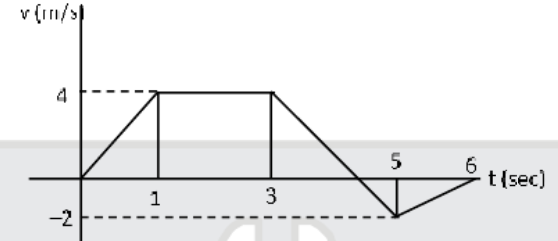 View Solution
View SolutionIf a particle moves from point P(2,3,5) to point Q(3,4,5). Its displacement vector be
View SolutionIn the diagram shown, a particle is moving from the point A to the point B. Length of each arrow is 1 m and the particle is moving at a constant speed of 1ms−1 . What is the displacement of the particle?
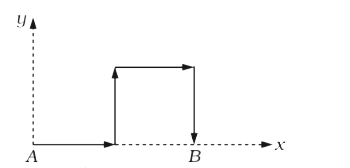 View Solution
View SolutionA particle starts from the origin, goes along the X-axis to the point (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionA particle is given a horizontal velocity u, from the point P on a smooth horizontal floor which has a vertical circular track at the end. ABC is a semicircular track of radius r in the vertical plane. If the path length PA is x=3r and the particle returns to point P, then the initial speed of the particle is
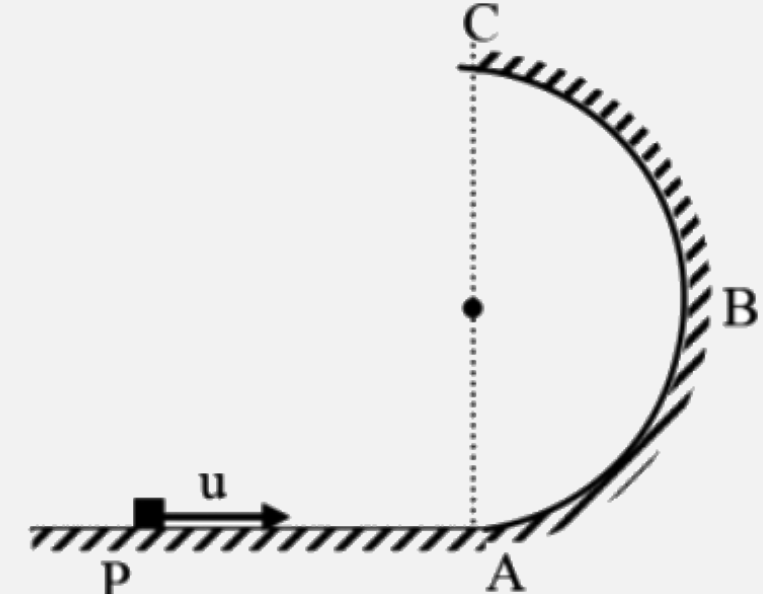 View Solution
View SolutionVelocity of a particle varies with time as v=atˆi+2ht2ˆj. If the particle starts from point (0,c), the trajectory of the particle is
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
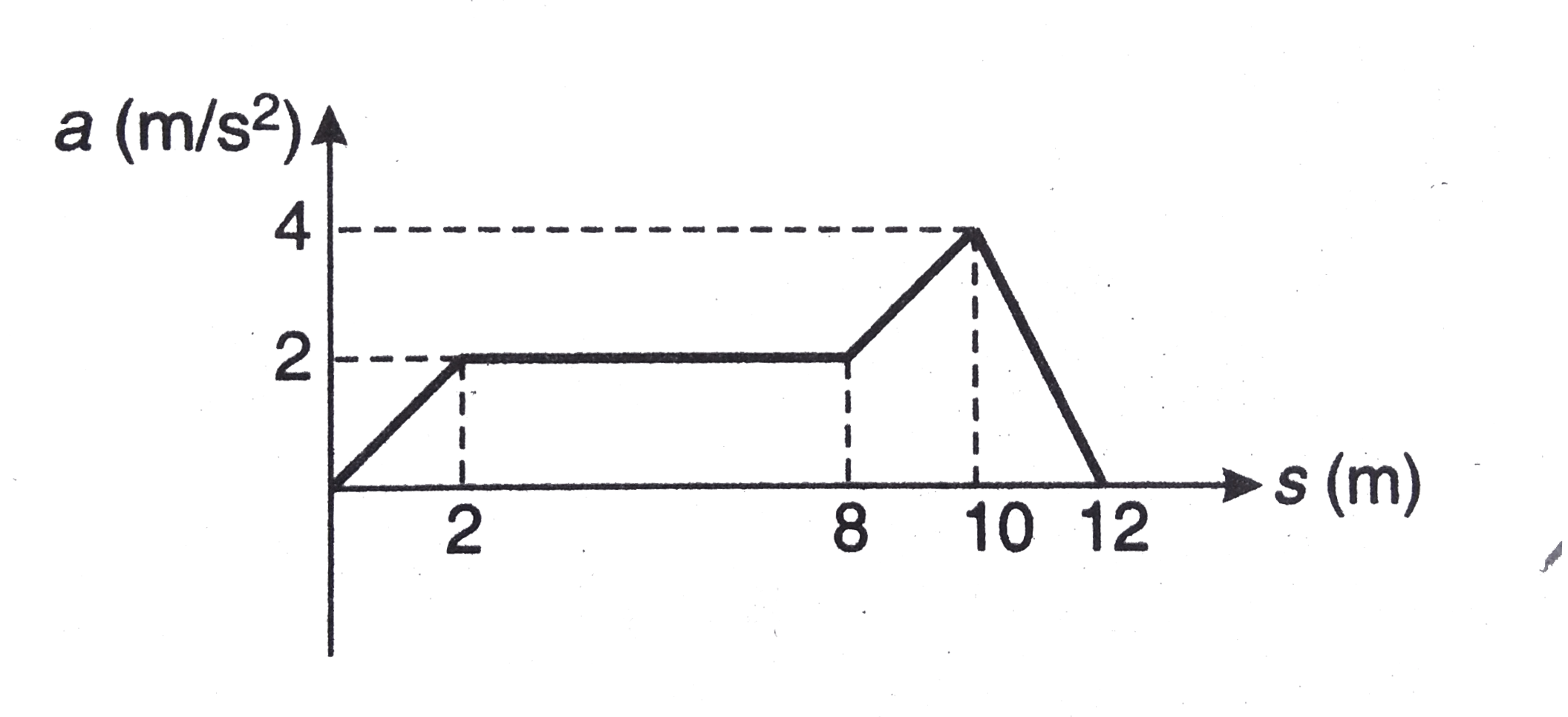 View Solution
View SolutionA particle is dropped from point P at time t = 0. At the same time another particle is thrown from point O as shown in the figure and it collides with the particle P. Acceleration due to gravity is along the negative y-axis. If the two particles collide 2 s after they start, find the initial velocity v0 of the particle which was projected from O. Point O is not necessarily on ground.
 View Solution
View Solution

