A particle starts from the origin, goes along the X-axis to the point (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
The correct Answer is:A, B, C, D
To solve the problem, we need to calculate both the distance and the displacement of the particle during its trip.
Step 1: Understand the motion of the particle
The particle starts at the origin (0, 0), moves to the point (20 m, 0), and then returns to the point (-20 m, 0).
Step 2: Calculate the displacement
Displacement is defined as the straight-line distance from the initial position to the final position, along with the direction.
- Initial position (O) = (0, 0)
- Final position (B) = (-20 m, 0)
To find the displacement:
Displacement = Final position - Initial position
Displacement = (-20 m) - (0 m) = -20 m
The negative sign indicates that the final position is 20 meters in the negative x-direction from the origin.
Step 3: Calculate the distance
Distance is the total length of the path traveled by the particle, regardless of direction.
1. Distance from the origin to point A (20 m, 0):
- Distance = 20 m (in the positive x-direction)
2. Distance from point A (20 m, 0) to point B (-20 m, 0):
- Distance = 20 m to return to the origin + 20 m to reach (-20 m, 0) = 40 m
Total distance traveled = Distance to A + Distance to B
Total distance = 20 m + 40 m = 60 m
Final Results
- Displacement = -20 m
- Distance = 60 m
The particle starts at the origin (0, 0), moves to the point (20 m, 0), and then returns to the point (-20 m, 0).
Displacement is defined as the straight-line distance from the initial position to the final position, along with the direction.
- Final position (B) = (-20 m, 0)
Displacement = Final position - Initial position
Displacement = (-20 m) - (0 m) = -20 m
Distance is the total length of the path traveled by the particle, regardless of direction.
- Distance = 20 m (in the positive x-direction)
- Distance = 20 m to return to the origin + 20 m to reach (-20 m, 0) = 40 m
Total distance = 20 m + 40 m = 60 m
- Displacement = -20 m
- Distance = 60 m
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
9 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
Similar Questions
A particle starts from the origin, goes along x-axis to the point (10 m, 0) and then returns along. The same line to the point (-10 m, 0). The distance and displacement of the particle during the trip are
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
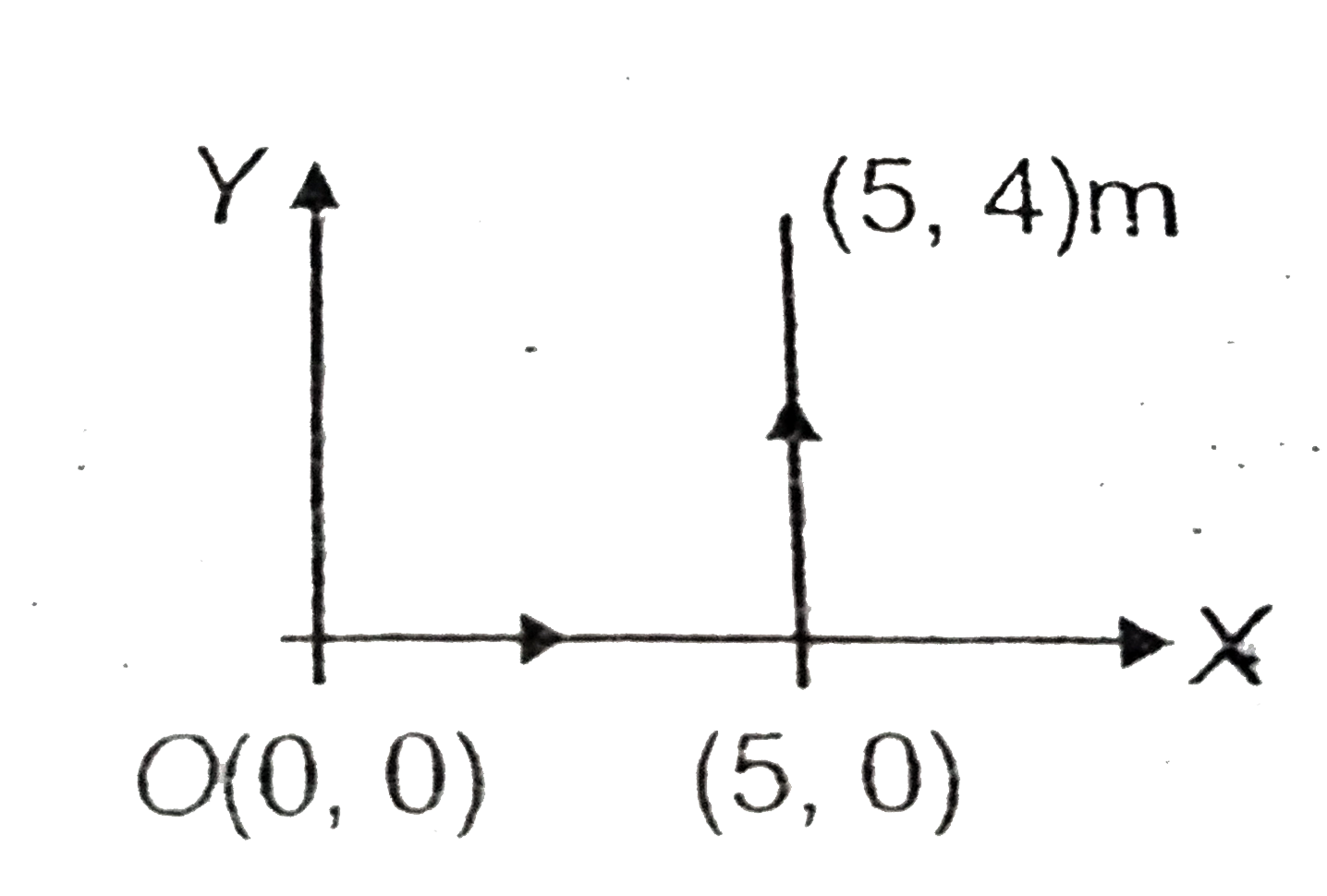
View SolutionA force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA particle starts from origin and moving along x−axis. Whose v−t graph is as shown . Choose the INCORRECT statement :
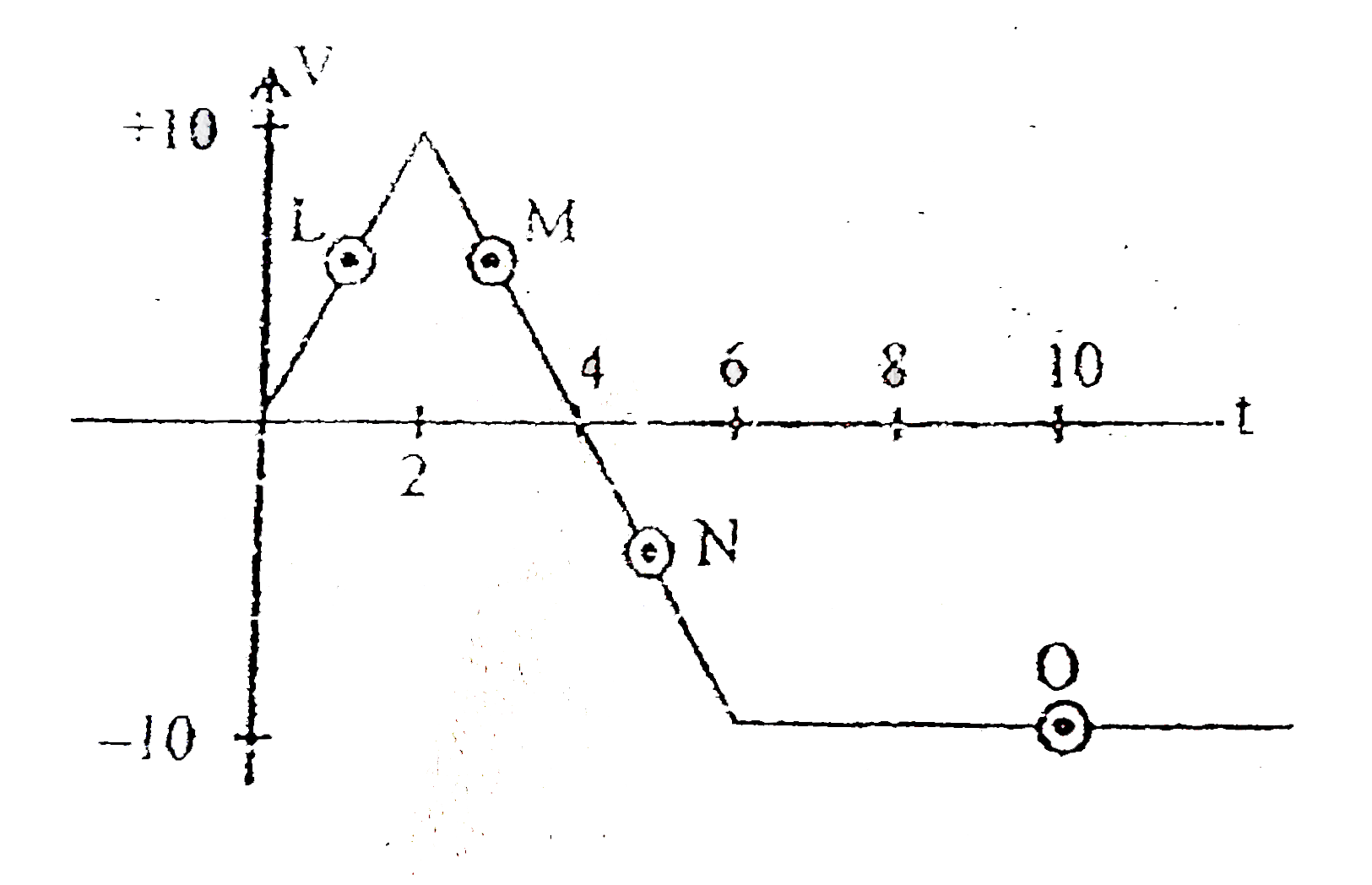 .
.
View SolutionTwo particles A and B start from the origin along x-axis. Velocity time graph of both particles are shown in the figure. During the given time interval, the maximum separation between the particles is
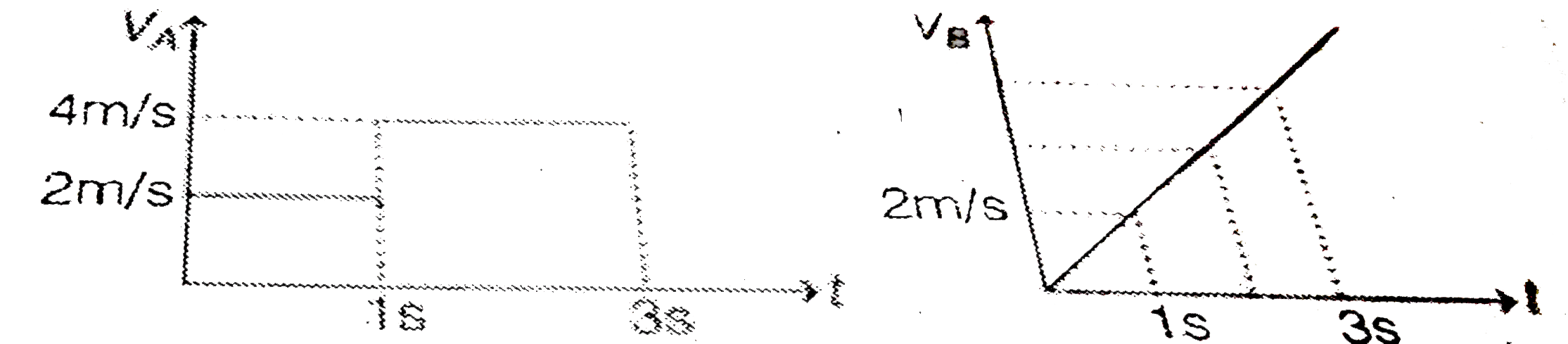
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View SolutionA particle moves on a straight line with velocity 2 m/s covers a distance of 5 m, returns back to initial position along same path with velocity 4 m/s. The distance and displacement covered by particle are respectively.
View SolutionThree particles start from the origin at the same time, one with a velocity v1 along the x-axis, second along the y-axis with a velocity v2 and third particle moves along the line x = y. The velocity of third particle, so that three may always lie on the same line is:
View SolutionA person moves 30 m along north direction, then moves 40 m along east direction and finally moves 20 m along south direction. Find distance & displacement
View SolutionFind the distance of the point (2,3) from the line 2x−3y+9=0 measured along a line x−y+1=0.
View Solution
