The potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with coordinates (3,3), only under the action of potential field force. Then its kinetic energy T at the instant when the particle is at a point with the coordinates (1,1) is
8α
24α
16α
Zero
The correct Answer is:8
To solve the problem, we need to calculate the kinetic energy of a particle moving under a potential energy field described by the equation U=α(x2+y2). The particle moves from the point (3, 3) to the point (1, 1). We will use the conservation of mechanical energy, which states that the total mechanical energy (kinetic energy + potential energy) remains constant in a conservative force field.
1. Identify Initial and Final Points:
- Initial point: (xi,yi)=(3,3)
- Final point: (xf,yf)=(1,1)
2. Calculate Initial Potential Energy:
- Using the potential energy formula U=α(x2+y2):
Ui=α(32+32)=α(9+9)=18α
3. Calculate Final Potential Energy:
- Calculate the potential energy at the final point:
Uf=α(12+12)=α(1+1)=2α
4. Calculate Change in Potential Energy:
- The change in potential energy ΔU is given by:
ΔU=Uf−Ui=2α−18α=−16α
5. Apply Conservation of Mechanical Energy:
- According to the conservation of energy:
ΔT+ΔU=0
- Rearranging gives:
ΔT=−ΔU
- Substituting the value of ΔU:
ΔT=−(−16α)=16α
6. Conclusion:
- The kinetic energy T at the instant when the particle is at point (1, 1) is:
T=16α
Final Answer:
The kinetic energy T at the instant when the particle is at the point (1, 1) is 16α.
---
- Initial point: (xi,yi)=(3,3)
- Final point: (xf,yf)=(1,1)
- Using the potential energy formula U=α(x2+y2):
Ui=α(32+32)=α(9+9)=18α
- Calculate the potential energy at the final point:
Uf=α(12+12)=α(1+1)=2α
- The change in potential energy ΔU is given by:
ΔU=Uf−Ui=2α−18α=−16α
- According to the conservation of energy:
ΔT+ΔU=0
- Rearranging gives:
ΔT=−ΔU
- Substituting the value of ΔU:
ΔT=−(−16α)=16α
- The kinetic energy T at the instant when the particle is at point (1, 1) is:
T=16α
The kinetic energy T at the instant when the particle is at the point (1, 1) is 16α.
Similar Questions
The potential energy of a particle is determined by the expression U=α(x2+y2), where α is a positive constant. The particle begins to move from a point with the co-ordinates (3, 3) only under the action of potential fields force. When it reaches the point
(1, 1) its kinetic energy is 4Kα. Find the value of K.
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View SolutionThe potential energy of a particle in a conservative field is U =a/r^3-b/r^2, where a and b are positive constants and r is the distance of particle from the centre of field. For equilibrium, the value of r is
View SolutionPotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) varsus position (x) graph is given, then
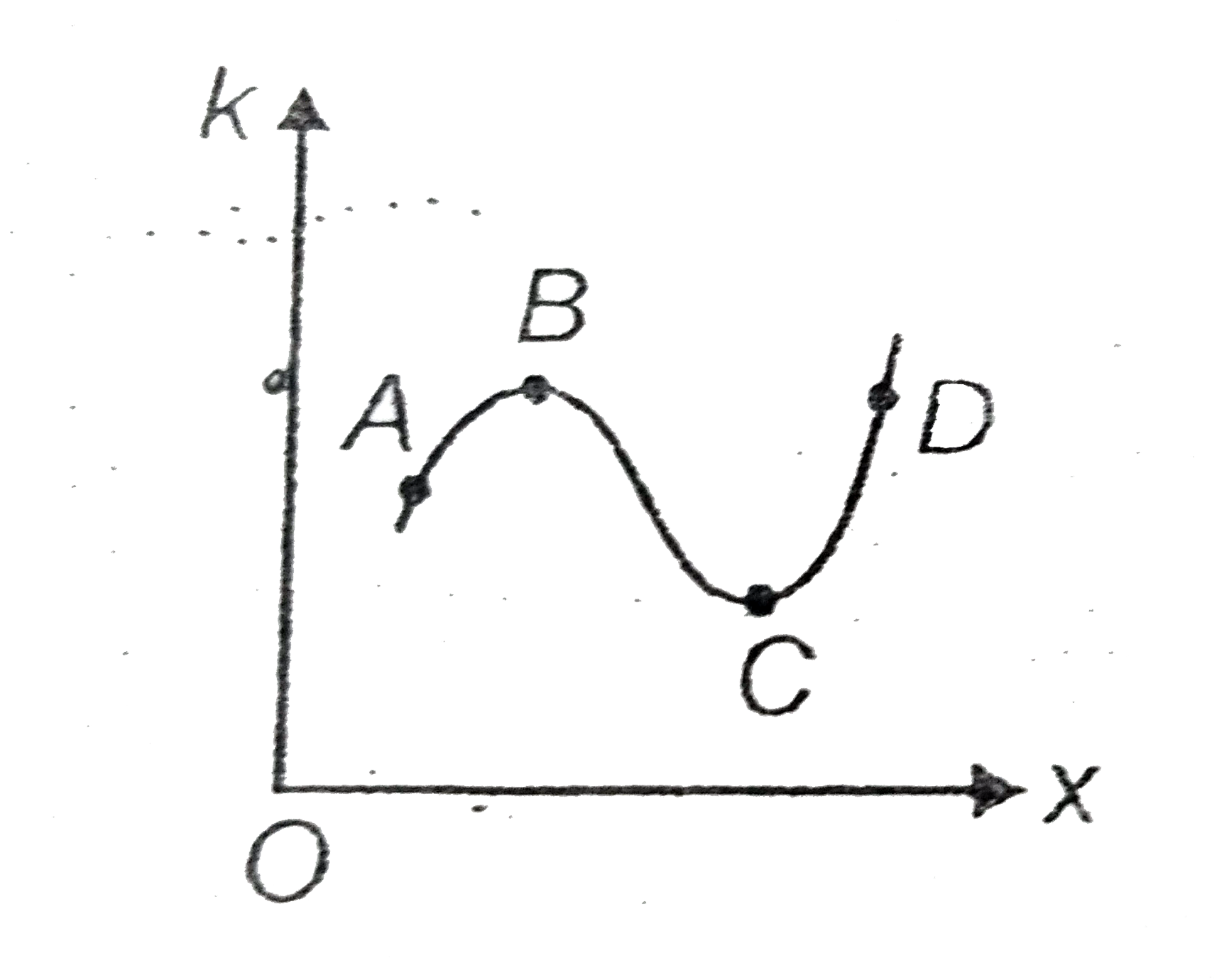
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionPotential energy of a particle is related to x coordinate by equation x2−2x . Particle will be in stable equilibrium at :
View SolutionFor a particle moving under the action of a variable force, kinetic energy (k) versus position (x) graph is given, then

View Solution
