A small spherical solid ball is dropped from a great height in a viscous liquid. Its journey in the liquid is best described in the diagram given below by the
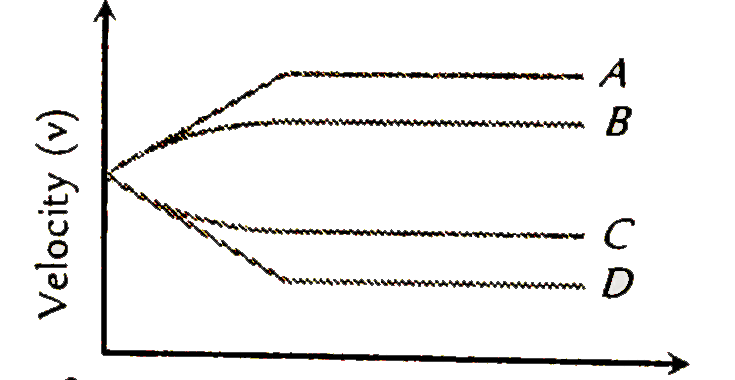
curve A
curve B
curve C
curve D
The correct Answer is:C
Step by step video & image solution for A small spherical solid ball is dropped from a great height in a viscous liquid. Its journey in the liquid is best described in the diagram given below by the by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A small spherical solid ball is dropped in a viscous liquid. It journey in the liquid is best described in the Fig. 15.5.1 by

View SolutionA small metallic spherical ball is dropped from a height h. If it collides with the ground inelastically and rebounds, then
View SolutionA particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
View SolutionA small tiny lead shot is gently dropped on the surface of a viscous liquid
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionA small lead ball is falling freely in a viscous liquid The velocity of the ball
View SolutionA spherical ball is dropped in a long column of a viscous liquid. The speed of the ball as a function of time may be best represented by the graph

View SolutionA small sphere falls from rest in a viscous liquid. Due to friction, heat is produced. Find the relation between the rate of production of heat and the radius of the sphere at terminal velocity.
View SolutionA spherical ball is dropped in a long column of viscous liquid. Which of the following graphs represent the variation of

(l) gravitational force with time
(ii) viscous force with time
(iii) net force acting on the ball with time
View SolutionA small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The ball will reach at the bottom of the vessel
View Solution
