A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.
![A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as rho(L)=rho(0)[4-(3h//h(0))].The density of the ball is (5//2)rho(0). The height of the vessel is h(0)=12//pi^(2) Consider r lt lt h(0) and g = 10 m//s^(2). The ball will reach at the bottom of the vessel](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_C04_E01_187_Q01.png)
The ball will reach at the bottom of the vessel
in 1s
in 2s
in 0.5s
the ball will not reach at the bottom of the vessel
The correct Answer is:A
Let the net force on this particle be zero at height h. Then weight
= upthrust (at h)
⇒43πr3g52ρ0−43πr2gρ0[4−3hh0]
⇒3hh0=4−52=32⇒h=h02………..i
Therefore, at h=h02, the equilibrium position, the particle has a speed in downward direction due to which it will move downward. Let at a further depth x from h02.

Fnet= upthrust − weight
=43πr3gρ0⎡⎢
⎢⎣4−3(h02−x)h0⎤⎥
⎥⎦−43πr3g52ρ0
=43πr3ρ0g[4−32+3xh0−52]=4πr3ρ0gh0x
∴F=4πr3ρ0gh0x
Since the net force on the and displacement of ball from its mean position are oppositely directed the particle executes SHM about its mean position i.e. h=h02
∴F=ma=−4πr3ρ0gh0x
=43πr352ρ0a=−4πr3ρ0gh0x
⇒a=−6g5h0x=−(12h0)x=−ω2x
where ω=√12h0=s√1212πr2=π
Hence, time taken by the particle to reach the bottom is
t=T2=122πω=πω=ππ=1s
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE13videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The motion of the ball in the vessel isView SolutionA small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

Where will the ball come in the equilibrium?View SolutionA uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as ρ=ρ0(1+hh0) where h is depth from free surface. Density of sphere σ will be :
 View Solution
View SolutionA small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as ρ=ρ02(α+βh). Mass of the ball is m. Select the most appropriate one option.
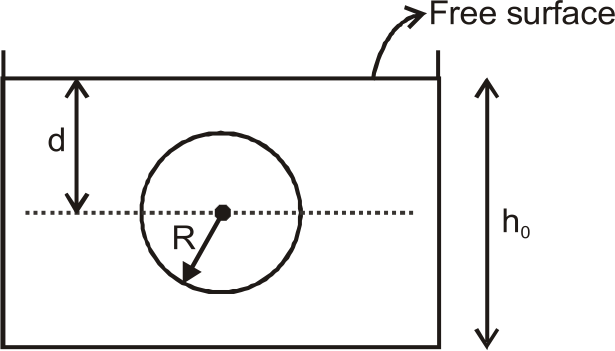
View SolutionA vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is
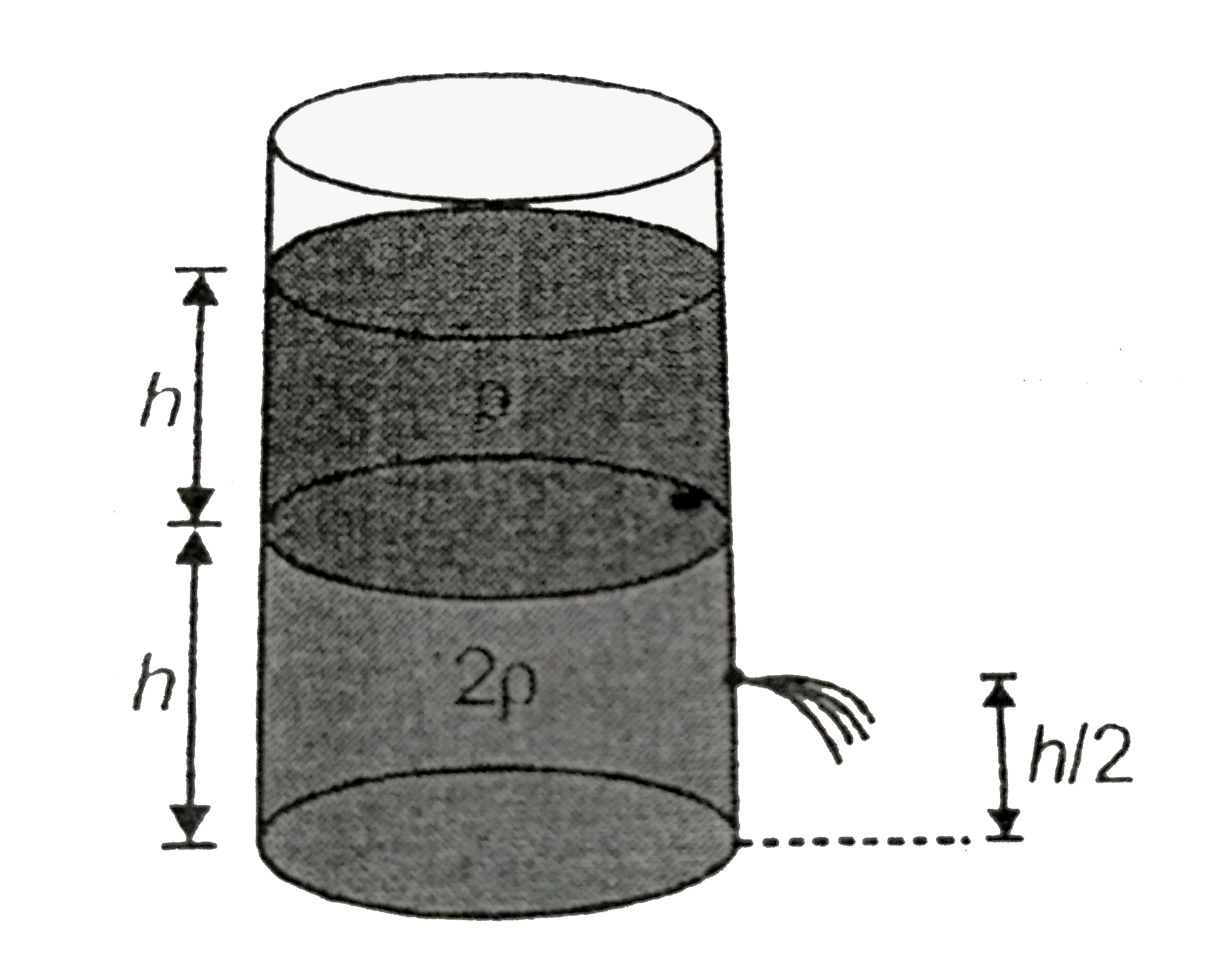 View Solution
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
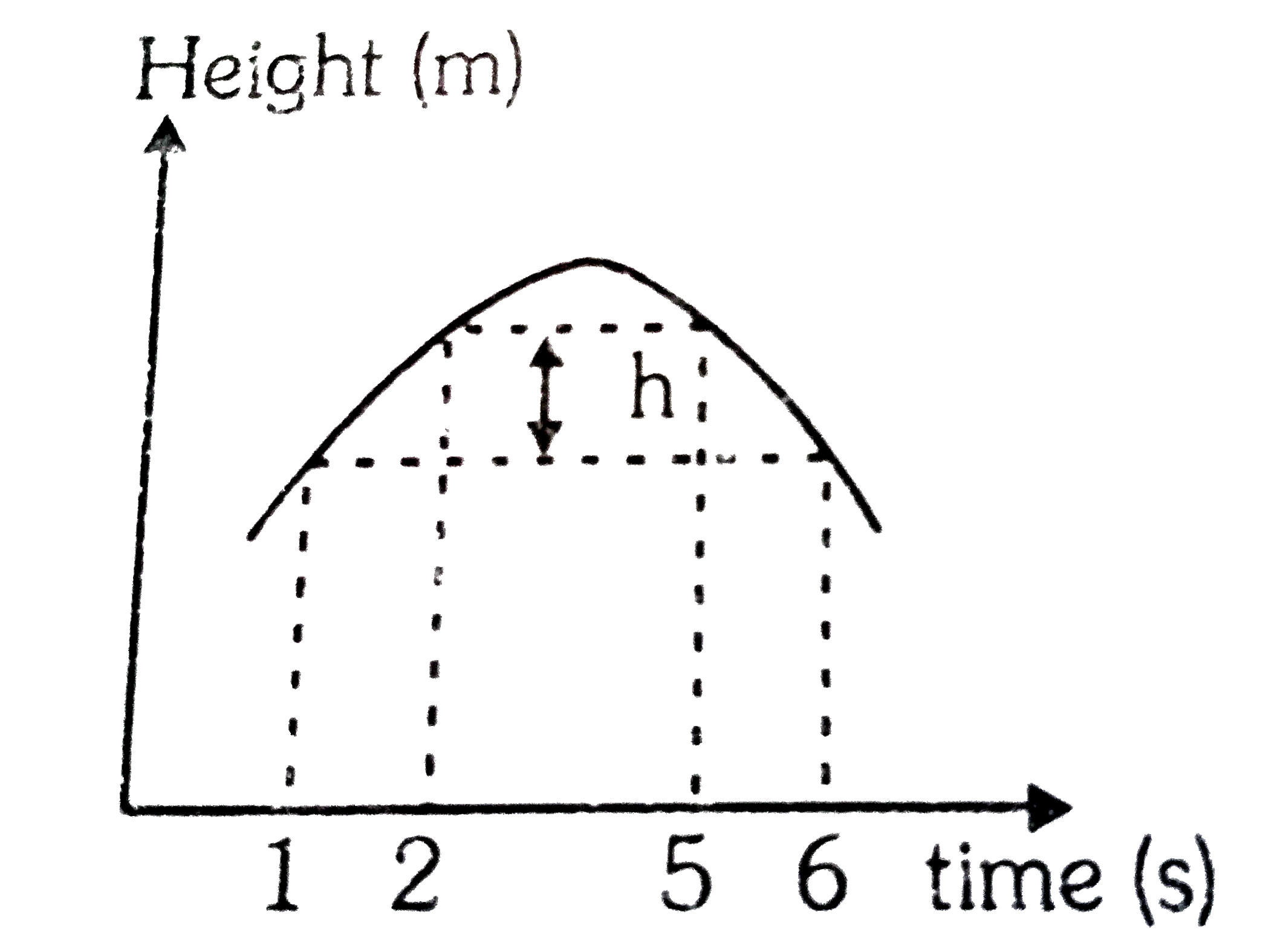 View Solution
View SolutionA sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ρ is the density of water]-
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )
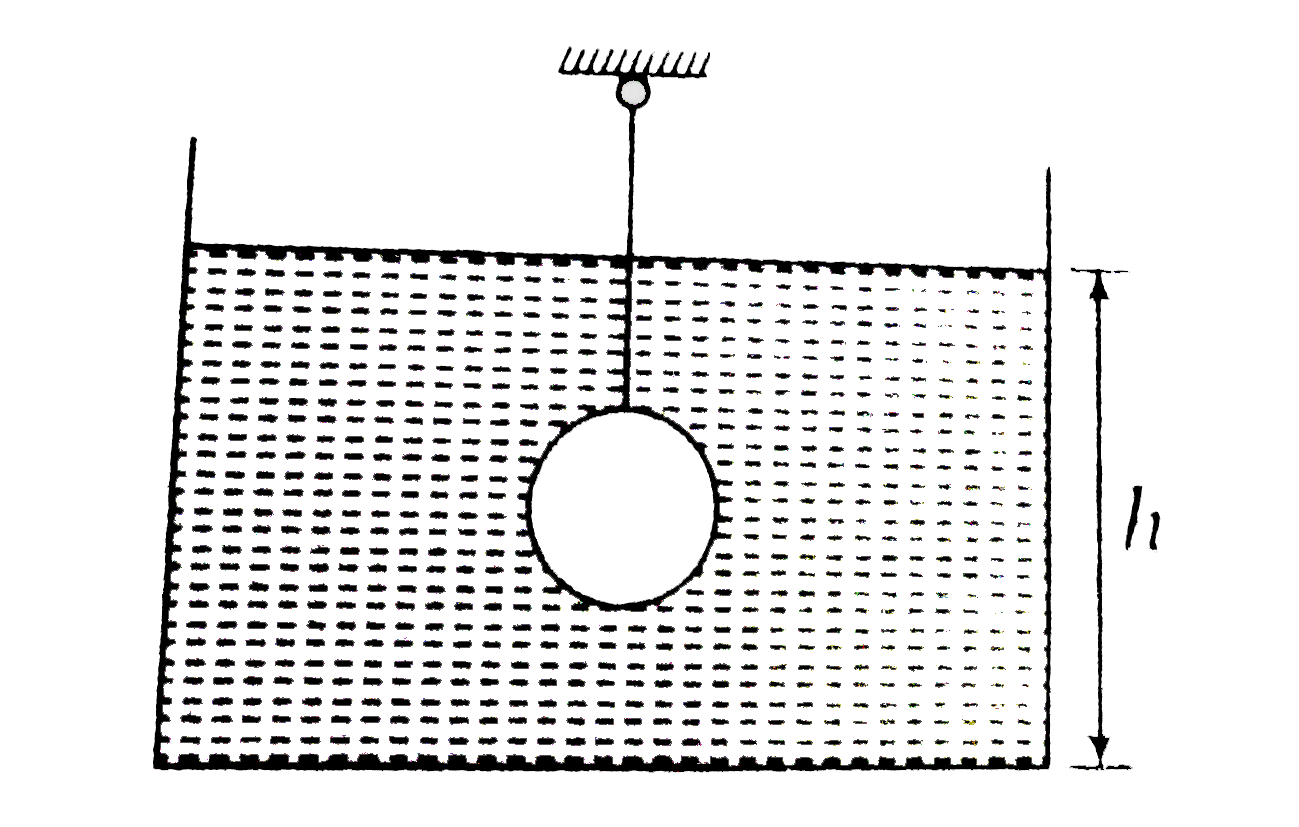 View Solution
View Solution

