A particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
The correct Answer is:u=√3GMR
To find the minimum velocity required for a particle of mass m to escape from the gravitational field of a solid sphere of mass M and radius R, we can follow these steps:
Step 1: Understand the gravitational potential inside the sphere
The gravitational potential V at a distance r from the center of a solid sphere of mass M and radius R is given by:
V(r)=−GMR+GM2R(3r−r2R)
At the center of the sphere (r=0):
V(0)=−3GM2R
Step 2: Set up the energy conservation equation
To escape the gravitational field, the particle must have enough kinetic energy to overcome the gravitational potential energy. The total mechanical energy at the center (initial) must equal the total mechanical energy at infinity (final). At infinity, the potential energy is zero, and we want the final kinetic energy to also be zero.
The conservation of energy can be expressed as:
Initial Kinetic Energy+Initial Potential Energy=Final Kinetic Energy+Final Potential Energy
This simplifies to:
12mv20+mV(0)=0
Step 3: Substitute the potential energy at the center
Substituting V(0):
12mv20−3GMm2R=0
Step 4: Solve for the minimum velocity v0
Rearranging the equation gives:
12mv20=3GMm2R
Dividing both sides by m (mass of the particle) and multiplying by 2:
v20=3GMR
Taking the square root:
v0=√3GMR
Conclusion
The minimum velocity required for the particle to escape from the gravitational field of the sphere is:
v0=√3GMR
The gravitational potential V at a distance r from the center of a solid sphere of mass M and radius R is given by:
V(r)=−GMR+GM2R(3r−r2R)
At the center of the sphere (r=0):
V(0)=−3GM2R
To escape the gravitational field, the particle must have enough kinetic energy to overcome the gravitational potential energy. The total mechanical energy at the center (initial) must equal the total mechanical energy at infinity (final). At infinity, the potential energy is zero, and we want the final kinetic energy to also be zero.
Initial Kinetic Energy+Initial Potential Energy=Final Kinetic Energy+Final Potential Energy
This simplifies to:
12mv20+mV(0)=0
Substituting V(0):
12mv20−3GMm2R=0
Rearranging the equation gives:
12mv20=3GMm2R
Dividing both sides by m (mass of the particle) and multiplying by 2:
v20=3GMR
Taking the square root:
v0=√3GMR
The minimum velocity required for the particle to escape from the gravitational field of the sphere is:
v0=√3GMR
Similar Questions
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
AGMRB−GMRC−4GMRD−2GMR - Question 2 - Select One
A particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
A−3GMRB−2GMRC−GMRD−4GMR
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the center.
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
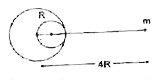 View Solution
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA particle of mass m was transferred from the centre of the base of a uniform hemisphere of mass M and radius R into infinity.
What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
View Solution

