The gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
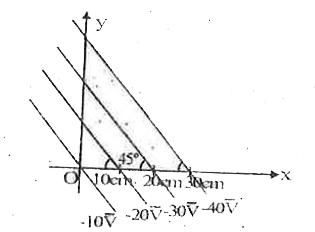
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
Speed of the particle (v) (y is in cm and v in cm/s) as function of its y-co-ordinate is
v=2√y
v=√2y
v=2y
v=2y+4y2+2y2
The correct Answer is:A
Step by step video & image solution for The gravitational field strength vecE and gravitational potential V are releated as vecE=-((deltaV)/(deltax)hati+(deltaV)/(deltay)hatj+(deltaV)/(deltaz)hatk) In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1vecV=1cm^(2)//s^(2) Speed of the particle (v) (y is in cm and v in cm/s) as function of its y-co-ordinate is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzhark)

In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
Speed of the particle (v) (y is in cm and v is in cm//s) as function of its y-co ordinate is
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
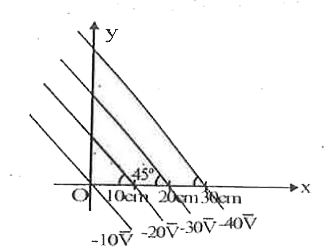
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
x-component of the velocity of the particle at the point (4cm,4cm) is
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
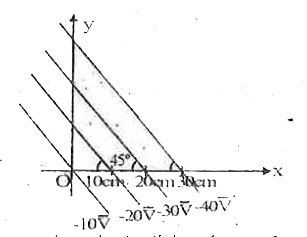
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
y-component of E a the point whose co-ordinates are (4cm,4cm) is
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
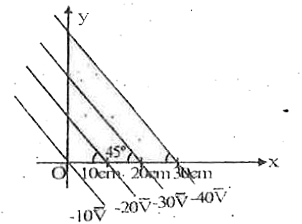
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
x-component of the velocity of the particle at the point (4cm,4cm) is
View SolutionA particle of mass 1 kg is released from rest at a point where gravitational potential is 5 J/kg. After some time, it passes through a point B with a speed of 1 m/s. What is the gravitational potential at B ?
View SolutionTwo particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi uniform magnetic field →B=−B0ˆk. If the particle passes through (0,y,0), then y is equal to
View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
A charge particle of mass 10 mg and charge 2.5μC is released from rest at x=2m. Find its velocity when it crosses origin.
View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.
View SolutionTwo point masses m and 2m are kept at points A and B as shown. E represents magnitude of gravitational field strength and V the gravitational potential. As we move from A to B

View Solution
