The gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
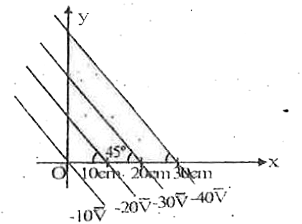
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
x-component of the velocity of the particle at the point (4cm,4cm) is
4cm/s
2cm/s
2√2cms
1cm/s
The correct Answer is:C
Step by step video & image solution for The gravitational field strength vecE and gravitational potential V are releated as vecE=-((deltaV)/(deltax)hati+(deltaV)/(deltay)hatj+(deltaV)/(deltaz)hatk) In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1vecV=1cm^(2)//s^(2) x-component of the velocity of the particle at the point (4cm,4cm) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
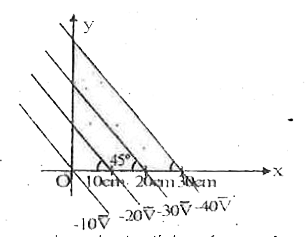
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
y-component of E a the point whose co-ordinates are (4cm,4cm) is
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzˆk)
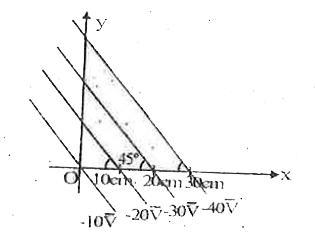
In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
Speed of the particle (v) (y is in cm and v in cm/s) as function of its y-co-ordinate is
View SolutionThe gravitational field strength →E and gravitational potential V are releated as
→E=−(δVδxˆi+δVδyˆj+δVδzhark)

In the figure, transversal lines represent equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential , 1→V=1cm2/s2
Speed of the particle (v) (y is in cm and v is in cm//s) as function of its y-co ordinate is
View SolutionA particle of mass 1 kg is released from rest at a point where gravitational potential is 5 J/kg. After some time, it passes through a point B with a speed of 1 m/s. What is the gravitational potential at B ?
View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
Draw the variation of electric field (E ) along the x-axis.
View SolutionWe know that electric field (E ) at any point in space can be calculated using the relation
→E=−δVδxˆi−δVδyˆj−δVδzˆk

if we know the variation of potential (V) at that point. Now let the electric potential in volt along the x-axis vary as V=2x2, where x is in meter. Its variation is as shown in figure
A charge particle of mass 10 mg and charge 2.5μC is released from rest at x=2m. Find its velocity when it crosses origin.
View SolutionInfinite number of bodies, each of mass 2kg, are situated on x-axis at distance 1m,2m,4m,8m......... respectively, from the origin. The resulting gravitational potential the to this system at the origing will be
View SolutionThe potential energy (in SI units) of a particle of mass 2kg in a conservative field is U=6x−8y. If the initial velocity of the particle is →u=−1.5ˆi+2ˆj, then find the total distance travelled by the particle in the first two seconds.
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionInfinite number of bodies, each of mass 2kg, are situated on x-axis at distance 1m,2m,4m,8m......... respectively, from the origin. The resulting gravitational potential due to this system at the origin will be
View Solution
