A ball of mass m = 1 kg rolling without slipping, strikes a smooth vertical wall and comes back. Before the impact the velocity of the ball is v1=10 cm/s and just after the impact v1=8 cm/s. Find the loss in energy of ball during the impact.
The correct Answer is:|ΔKE|=1.8×10−3J
To find the loss in energy of the ball during the impact with the wall, we will calculate the initial and final kinetic energies of the ball and then find the difference between them.
Step 1: Calculate Initial Kinetic Energy
The initial kinetic energy (KE_initial) of the ball can be calculated using the formula:
KE=12mv2
where:
- m=1kg (mass of the ball)
- v1=10cm/s=10×10−2m/s=0.1m/s (initial velocity)
Substituting the values:
KEinitial=12×1×(0.1)2=12×1×0.01=0.005J=5×10−3J
Step 2: Calculate Final Kinetic Energy
The final kinetic energy (KE_final) of the ball after it bounces back can be calculated similarly:
KEfinal=12mv′2
where:
- v′=8cm/s=8×10−2m/s=0.08m/s (final velocity)
Substituting the values:
KEfinal=12×1×(0.08)2=12×1×0.0064=0.0032J=3.2×10−3J
Step 3: Calculate Loss in Energy
The loss in energy during the impact can be calculated by finding the difference between the initial and final kinetic energies:
Loss in Energy=KEinitial−KEfinal
Substituting the values:
Loss in Energy=5×10−3J−3.2×10−3J=1.8×10−3J
Final Answer
The loss in energy of the ball during the impact is:
Loss in Energy=1.8×10−3J
---
The initial kinetic energy (KE_initial) of the ball can be calculated using the formula:
KE=12mv2
where:
- m=1kg (mass of the ball)
- v1=10cm/s=10×10−2m/s=0.1m/s (initial velocity)
KEinitial=12×1×(0.1)2=12×1×0.01=0.005J=5×10−3J
The final kinetic energy (KE_final) of the ball after it bounces back can be calculated similarly:
KEfinal=12mv′2
where:
- v′=8cm/s=8×10−2m/s=0.08m/s (final velocity)
KEfinal=12×1×(0.08)2=12×1×0.0064=0.0032J=3.2×10−3J
The loss in energy during the impact can be calculated by finding the difference between the initial and final kinetic energies:
Loss in Energy=KEinitial−KEfinal
Substituting the values:
Loss in Energy=5×10−3J−3.2×10−3J=1.8×10−3J
The loss in energy of the ball during the impact is:
Loss in Energy=1.8×10−3J
Similar Questions
Knowledge Check
A ball of mass m travelling horiozntally with velocity v strikes a massive vertical wall and rebounds back along its original direction with no change in speed. What is the magnitude of the impulse delivered by the wall to the ball?
A0B12mvCmvD2mv
A ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
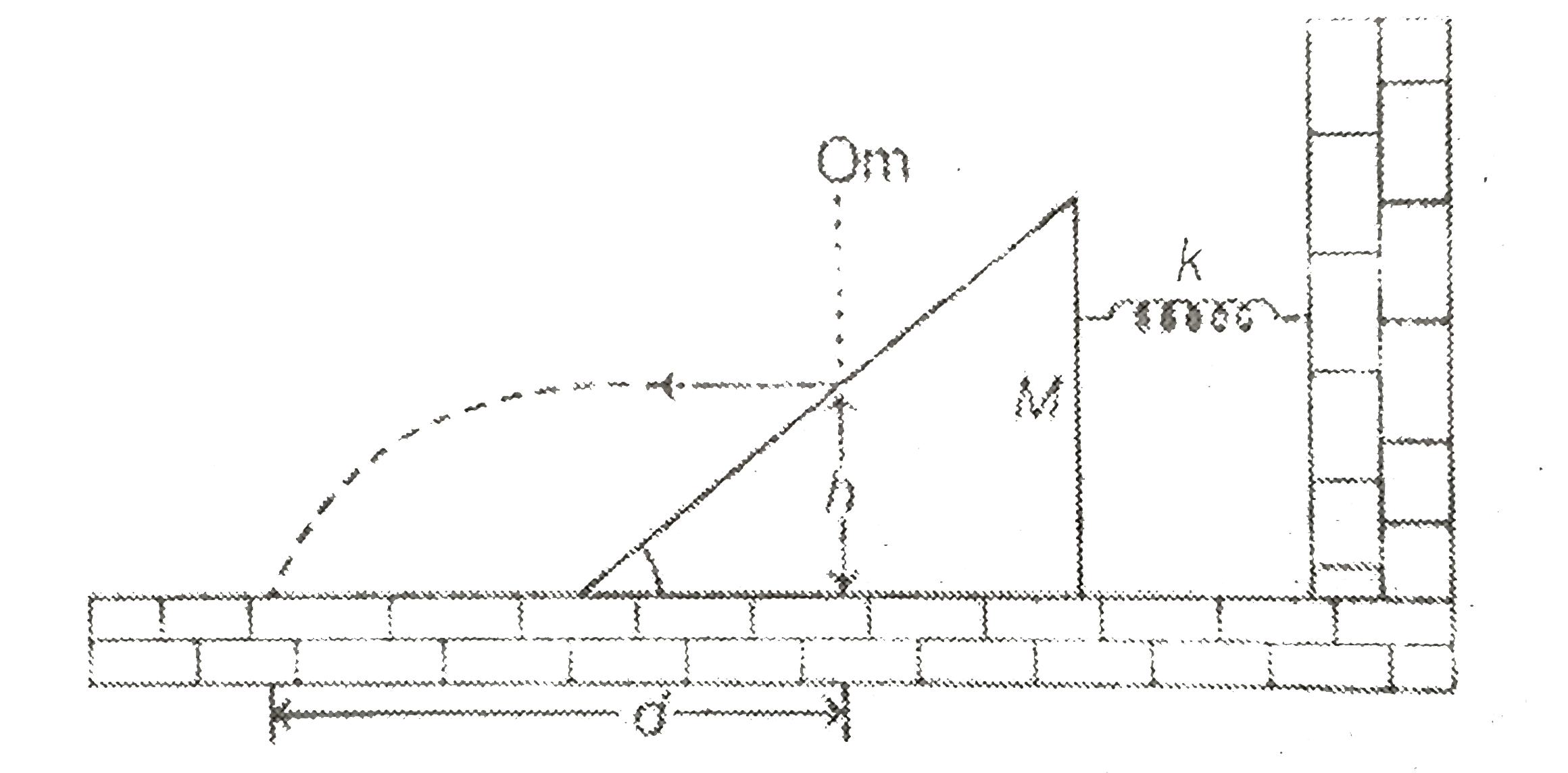
View SolutionA ball of mass m when dropped from certain height as shown in diagram, strikes a wedge kept on smooth horizontal surface and move horizontally just after impact. If the ball strikes the ground at a distance d from its initial line of fall, thenthe amplitude of oscillation of wedge after being hit by the ball will be
View SolutionA ball is thrown vertically upwards. It goes to a height 19.6 m and then comes back to the ground, Find the initial velocity of the ball .
Take g = 9.8 ms−2
View SolutionA ball of mass m collides with a stationary identical ball a speed v0. Find the impulse of the colliding balls (e=1/2).
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
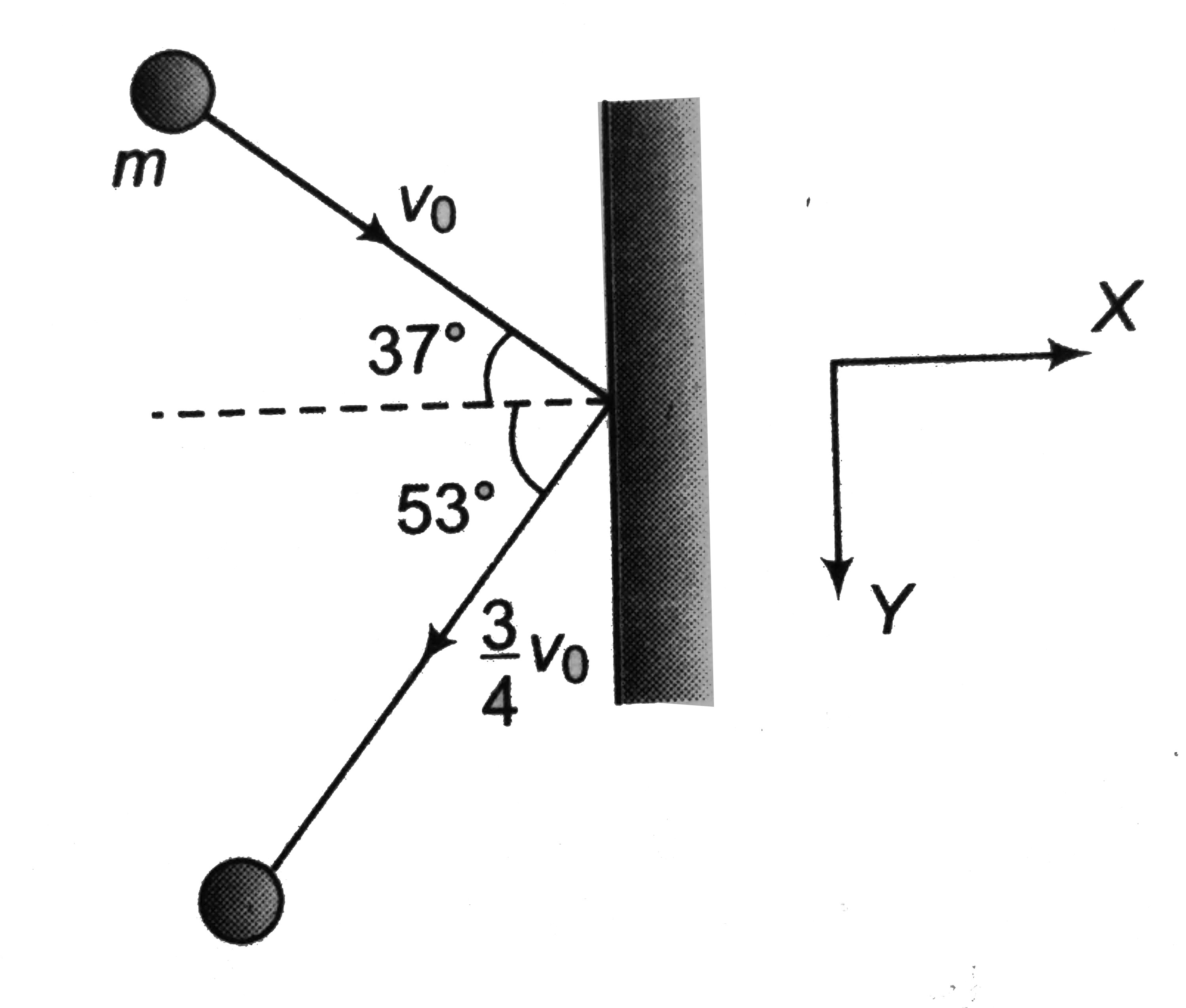
View SolutionA ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is
View Solution


 .
.