A coil of negligible resistance is connected inseries with 90Ω resistor acorss a 120 V -60 Hz line. A voltmeter reads 36 V across the resistance. Find voltage across the coil and inductance of the coil.
To solve the problem step-by-step, we will follow these calculations:
Step 1: Calculate the current (I) through the circuit
Given that the voltage across the resistor (V_R) is 36 V and the resistance (R) is 90 Ω, we can use Ohm's Law to find the current (I).
I=VRR=36V90Ω=0.4A
Step 2: Calculate the total impedance (Z) of the circuit
The total voltage (V) across the circuit is given as 120 V. We can find the total impedance (Z) using the formula:
Z=VI=120V0.4A=300Ω
Step 3: Calculate the inductive reactance (X_L)
Using the relationship between impedance (Z), resistance (R), and inductive reactance (X_L):
Z=√R2+X2L
We can rearrange this to find X_L:
XL=√Z2−R2=√3002−902
Calculating the squares:
XL=√90000−8100=√81900≈286.37Ω
Step 4: Calculate the inductance (L) of the coil
The inductive reactance (X_L) is related to the inductance (L) and the angular frequency (ω) by the formula:
XL=ωL
Where ω=2πf and f=60Hz:
ω=2π×60≈376.99rad/s
Now, substituting for X_L:
L=XLω=286.37376.99≈0.76H
Step 5: Calculate the voltage across the coil (V_L)
The voltage across the coil can be calculated using the formula:
VL=I⋅XL=0.4A×286.37Ω≈114.55V
Final Results
- Voltage across the coil (V_L) = 114.55 V
- Inductance of the coil (L) = 0.76 H
Given that the voltage across the resistor (V_R) is 36 V and the resistance (R) is 90 Ω, we can use Ohm's Law to find the current (I).
The total voltage (V) across the circuit is given as 120 V. We can find the total impedance (Z) using the formula:
Using the relationship between impedance (Z), resistance (R), and inductive reactance (X_L):
The inductive reactance (X_L) is related to the inductance (L) and the angular frequency (ω) by the formula:
The voltage across the coil can be calculated using the formula:
- Voltage across the coil (V_L) = 114.55 V
- Inductance of the coil (L) = 0.76 H
Similar Questions
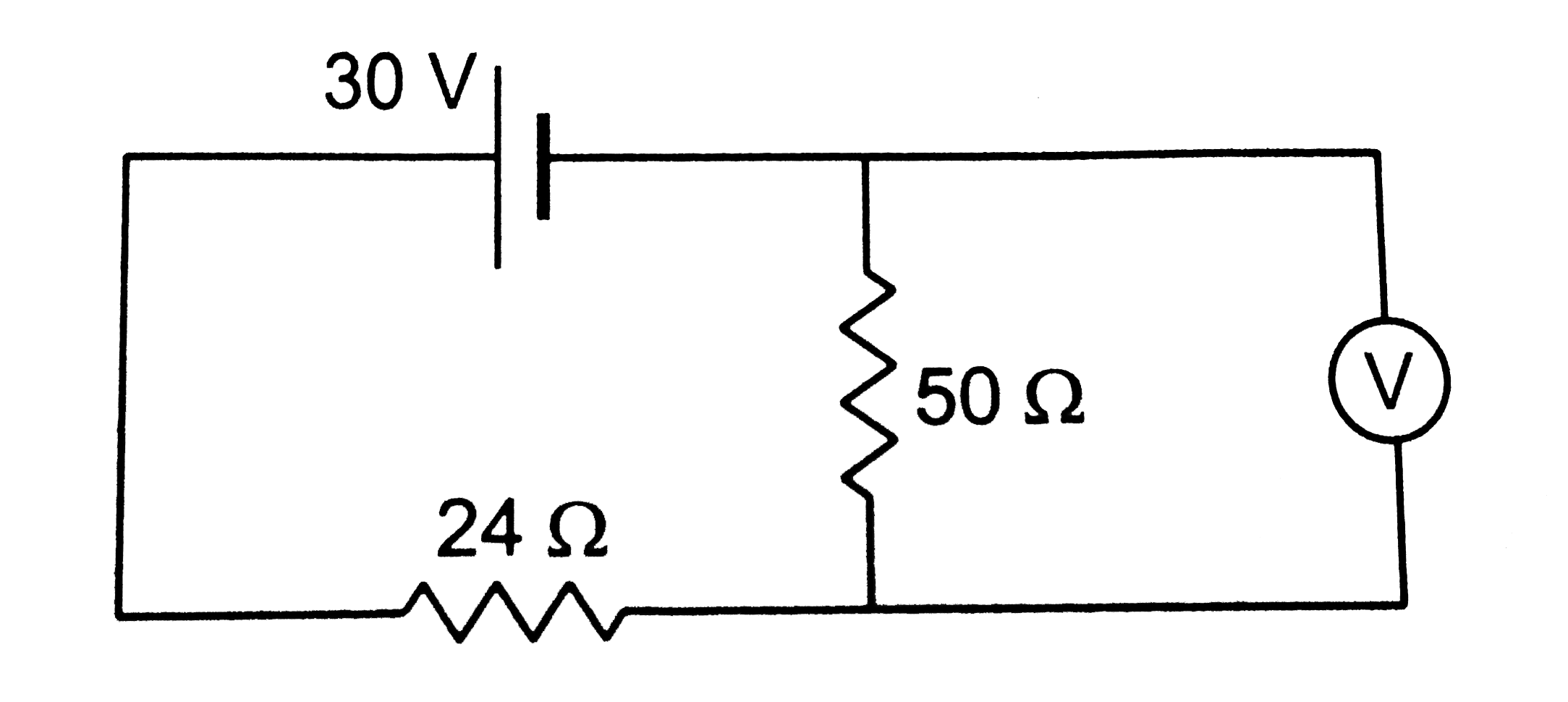
The voltmeter shown in figure reads 18V across the 50(Ω)resistor. Find the resistance of the voltmeter.
 View Solution
View SolutionAn alternating voltage is connected in series with a resistance R and inductance L if the potential drop across the resistance is 200V and across the inductance is 150V, then the applied voltage is
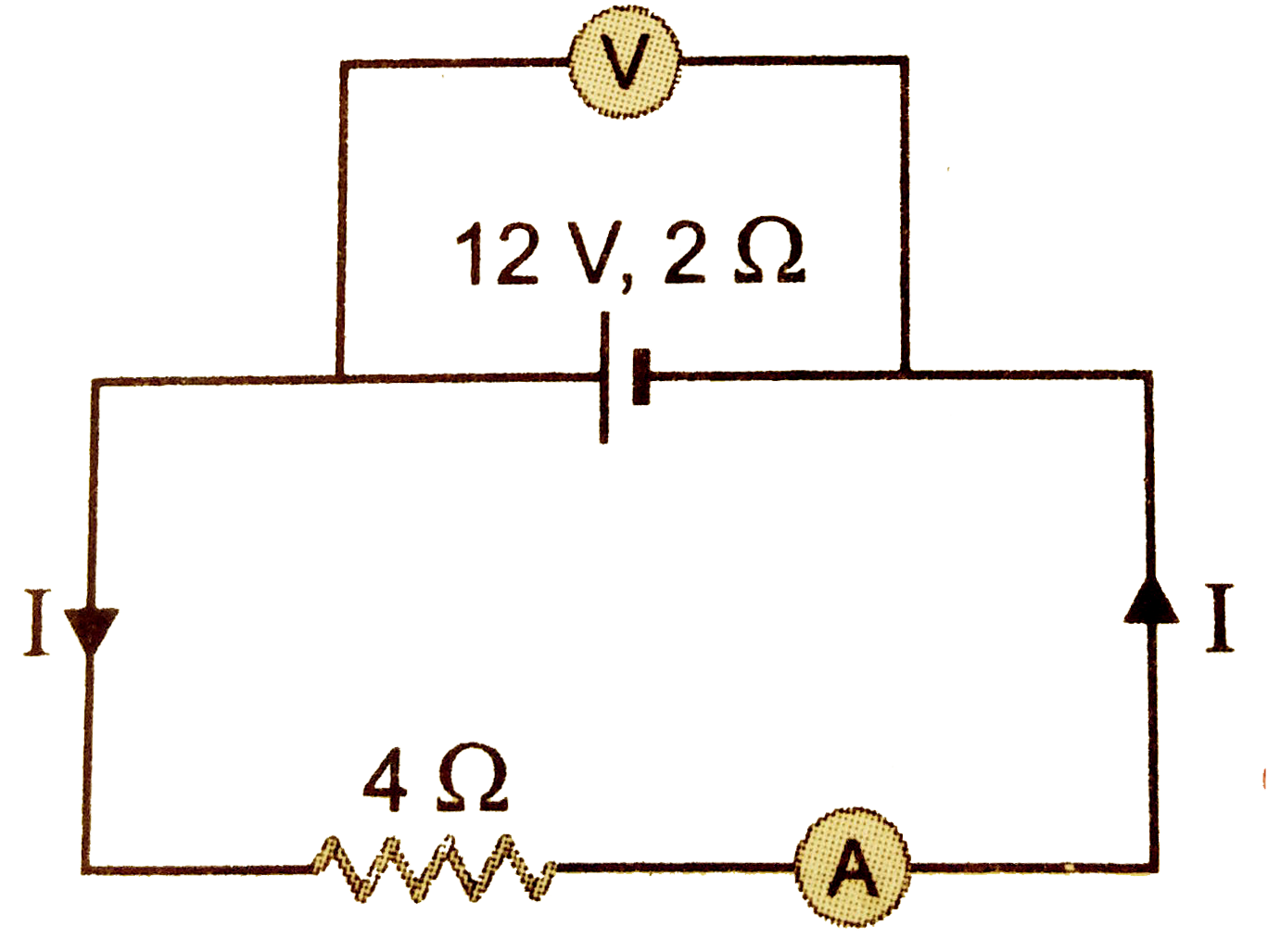
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
 View Solution
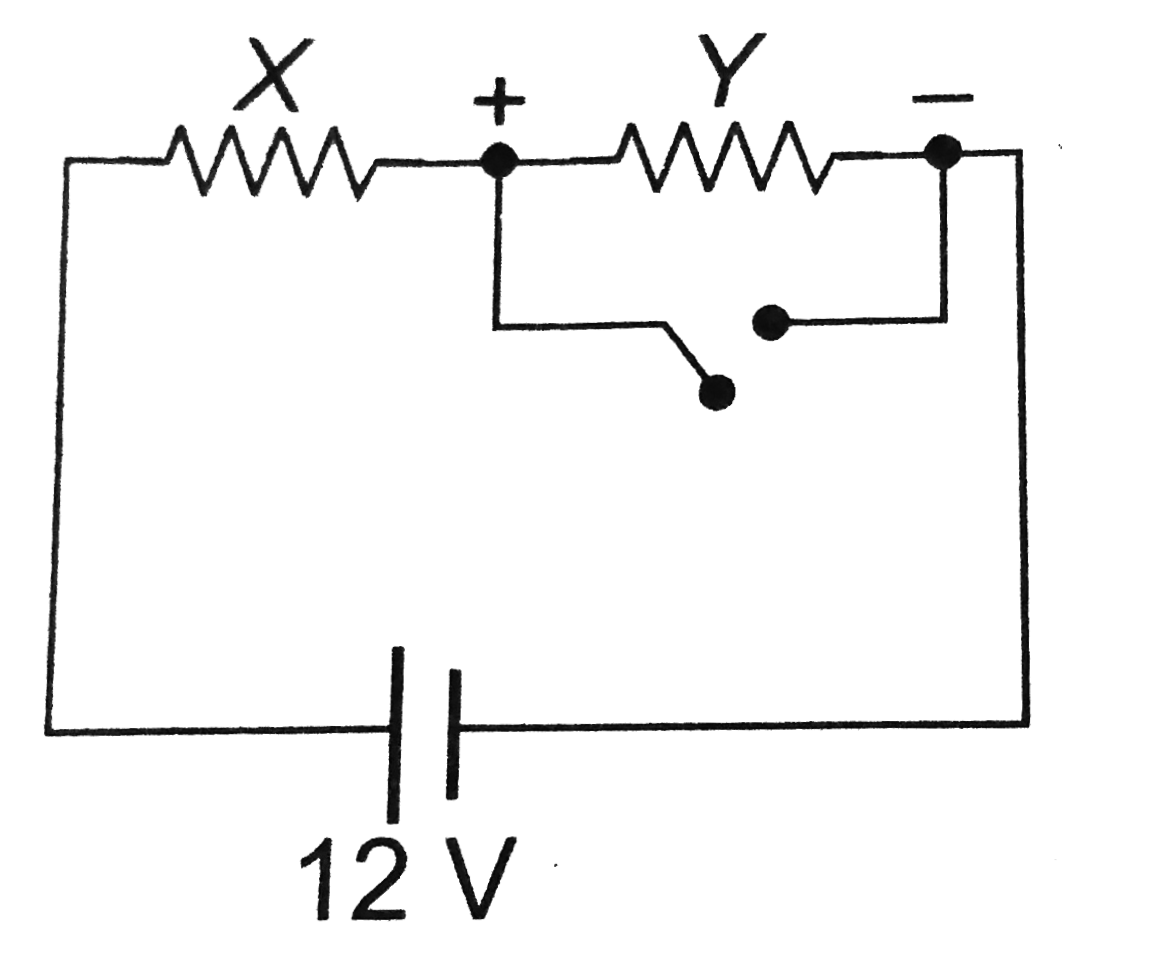
View SolutionWhen an ammter of negligible internal resistance is inserted in series with circuit it reads 1A When the voltmeter of very large resistance is connected across X it reads 1V. When the point A and B are shorted by a conducting wire, the voltmeter meausres 10V across the battery. The internal resistance of the battery is equal to
 View Solution
View SolutionA 10 V storage battery of negligible internal resistance is connected across a 50Ω resistor. How much heat energy is produced in the resistor in 1 hour
View SolutionA series circuit consisting of an inductance − free resistance R=0.16kΩ and coil with active resistance is connected to the mains with effective voltabe V=220V. Find the heat power generated in the coil if the effective voltage values across the resistance R and the coil are equal to V1=80V and V2=180V respectively.
View SolutionA 20volts AC is applied to a circuit consisting of a resistance and a coil with negligible resistance. If the voltage across the resistance is 12V, the voltage across the coil is
View SolutionA coil of resistance 40Ω is connected across a 4.0 V battery. 0.10 s after the battery is connected, the current in the coil is 63 mA. Find the inductance of the coil.
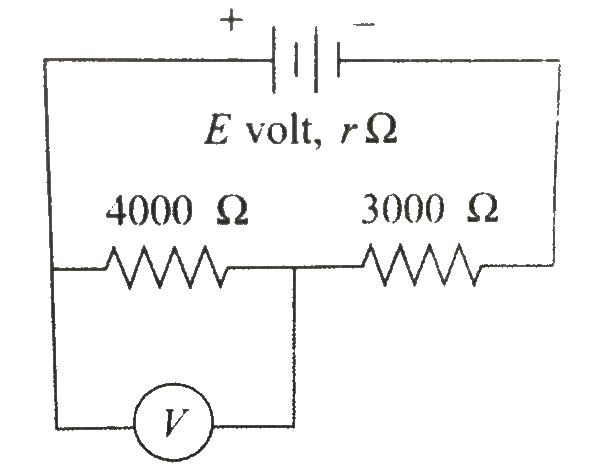
View SolutionIn Fig.6.59, when an ideal voltmetre is connected across 4000Ω resistance, it reads 30V. If the voltmeter is connected across 3000Ω resistance, it will read
 View Solution
View SolutionThe voltmeter shown in the figure reads 10V across 40 ω . The resistance of voltmeter is
View Solution

