The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
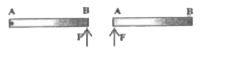
αA=αB
αA>αB
αA<αB
data insufficient to determine
The correct Answer is:C
Step by step video & image solution for The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation lambda = lambda_(0) x , where lambda_(0) is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is alpha_(A) and in the second case it is alpha_(B) then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
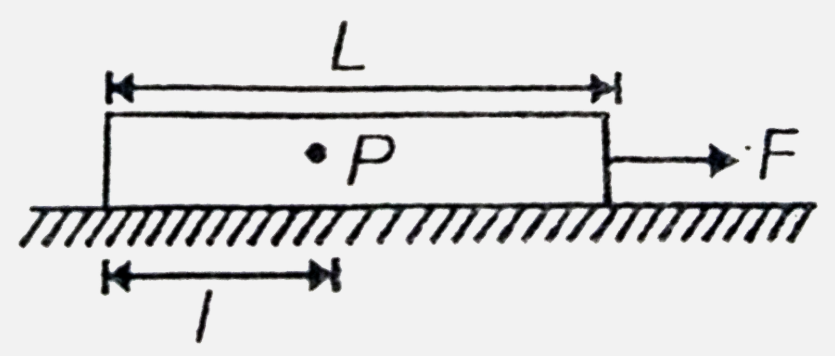
Figure shows a rope of variable mass whose linear mass density is given by , λ=Ax , where A is + ve constant and x is distance from left end . It bis placed on a smooth horizontal surface . A force F is acting on it as shown .
(i) Find total mass of the rope .
(ii) Find tension at point P.
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA rod hanging from ceiling has linear density given as λ=m0(1+x) kg/m, where m0 is constant and x is distance of a point from free end . if the length of the rod is 4m then velocity of wave at x=1m is
View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionYou are given a rod of length L. The linear mass density is λ such that λ=a+bx. Here a and b are constants and the mass of the rod increases as x decreases. Find the mass of the rod

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View Solution