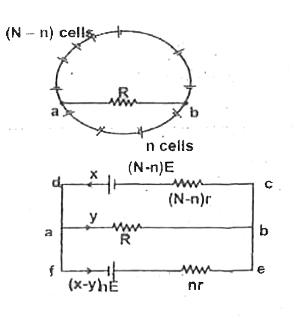
n' cells , each of emf 'e' and internal resistance 'r' are connected in a closed circuit so that the positive terminal of a cell is joined to the negative terminal of the next, as shown in figure. Any two points of the circuit are connected by an external resistance R. Find the current in R.
If n be the number of cells connected on one side of resistor R, then the number of cells connected on the other side of Ris (N - n). Current distribution in the equivalent circuit is shown in the adjoining circuit diagram
Here, n cells are shown as equivalent to a single cell of emf (N-n)E nE and internal resistance nr. Similarly, (N-n) cells are(N-n) shown equivalent to a single cell of emf (N-n)E and internal resistance (N-n)r. Applying Kirchoff.s second law to closed abcda X[N−n]r+yR=(N−n)E
X=(N−n)E−yR(N−n)r
X=(yN−n)Rr...(1)
Applying Kirchoff.s second law to closed mesh cdafebc
X(N−n)r+(x−y)nr=(N−n)E+nE
X[(N−n)r+nr]=NE+ynr
xNr=NE+ynr
xNE=ynr
x=NE+ynrnr
x=NE+ynrNr
x=Er+ynN
Combining Eqs (1) and (2), we get
vEr−(yN−n)Rr=Er+ynN
y[nN+Rn−nr]=0 ∴y=0
i.e. current through resistor R is zero. Alternate
Current in the ring I = E//rthereforeVa+nE−∈r=Vb Va−V−(b)=−nE+nr(E/r)=0 No current through the resistor R.
Similar Questions
n identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View Solutionn identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View Solution
Knowledge Check
- Question 1 - Select One
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
Two cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionFive cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
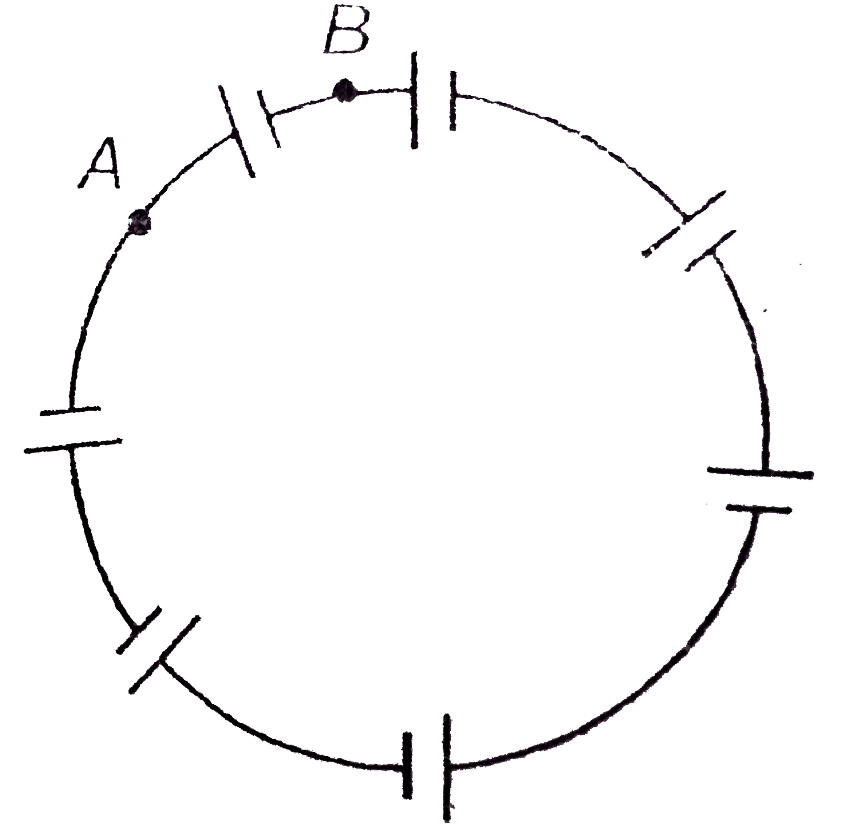 View Solution
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View SolutionA cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View Solution

