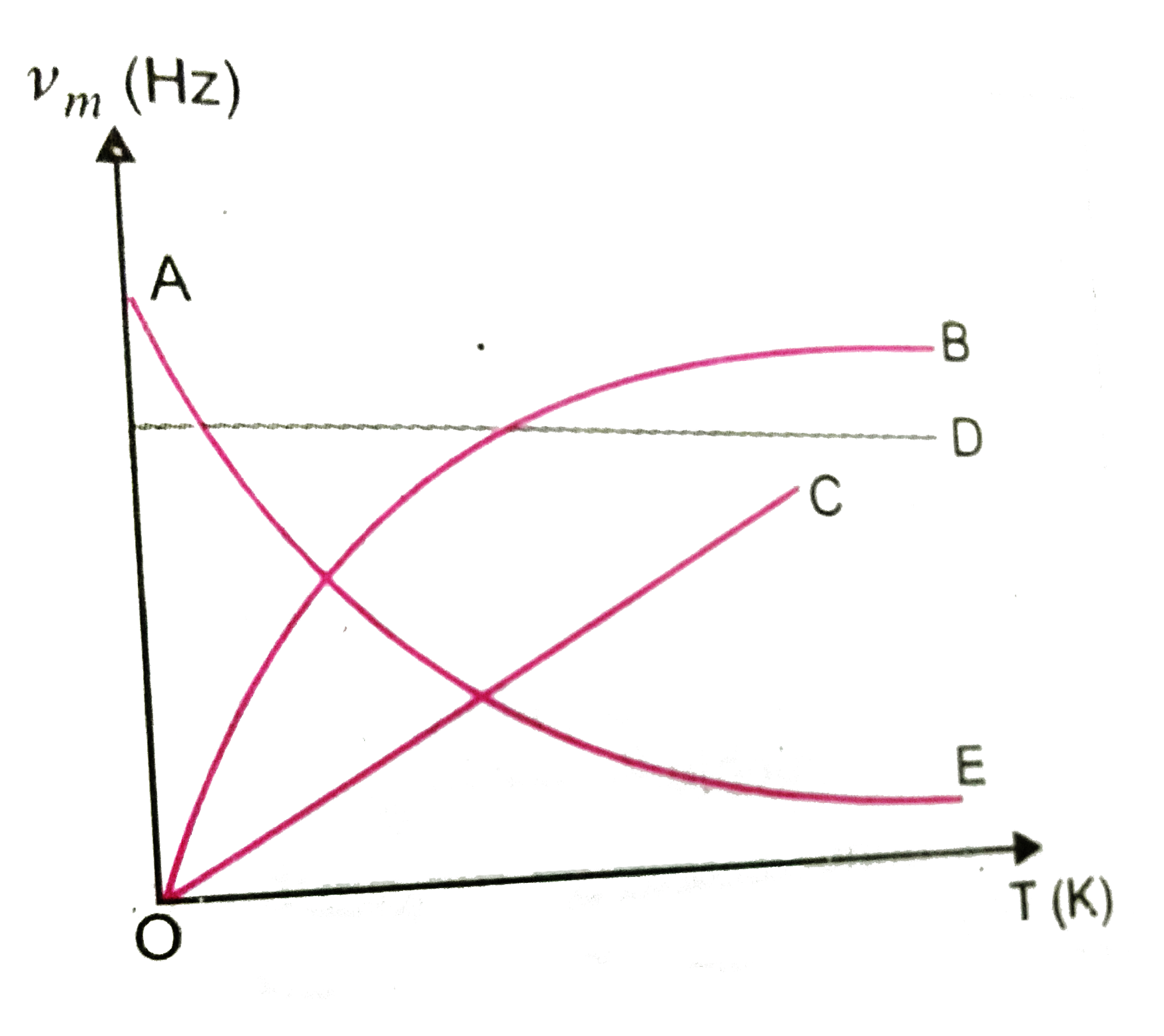
Which of the following is v-T graph for spectral distribution of radiance in a perfectly black body? (Where v is the frequency corresponding to maximum wavelength.)


The correct Answer is:C
To solve the question regarding the v-T graph for the spectral distribution of radiance in a perfectly black body, we can follow these steps:
1. Understand Wien's Displacement Law:
Wien's Displacement Law states that the product of the maximum wavelength (λm) of radiation emitted by a black body and its absolute temperature (T) is a constant (b). Mathematically, this is expressed as:
λm⋅T=b
2. Relate Wavelength to Frequency:
The relationship between wavelength (λ) and frequency (ν) is given by the equation:
λ=cν
where c is the speed of light. Therefore, we can express the maximum wavelength in terms of frequency:
λm=cνm
3. Substitute into Wien's Law:
Substituting the expression for λm into Wien's Law gives:
cνm⋅T=b
Rearranging this equation to solve for νm yields:
νm=cb⋅T
4. Identify the Relationship:
From the equation νm=cb⋅T, we can see that νm is directly proportional to T. This indicates that as the temperature increases, the frequency corresponding to the maximum wavelength also increases linearly.
5. Graph Interpretation:
Since νm is proportional to T, the graph of νm versus T will be a straight line with a positive slope. This means that if we were to plot the frequency (ν) on the y-axis and temperature (T) on the x-axis, we would expect a linear graph.
6. Select the Correct Option:
Based on the understanding that the graph must be linear with a positive slope, we can identify the correct option from the given choices. The option that represents a linear graph with a positive slope is the correct answer.
Conclusion:
The correct option for the v-T graph for the spectral distribution of radiance in a perfectly black body is the one that shows a linear relationship with a positive slope.
Wien's Displacement Law states that the product of the maximum wavelength (λm) of radiation emitted by a black body and its absolute temperature (T) is a constant (b). Mathematically, this is expressed as:
λm⋅T=b
The relationship between wavelength (λ) and frequency (ν) is given by the equation:
λ=cν
where c is the speed of light. Therefore, we can express the maximum wavelength in terms of frequency:
λm=cνm
Substituting the expression for λm into Wien's Law gives:
cνm⋅T=b
Rearranging this equation to solve for νm yields:
νm=cb⋅T
From the equation νm=cb⋅T, we can see that νm is directly proportional to T. This indicates that as the temperature increases, the frequency corresponding to the maximum wavelength also increases linearly.
Since νm is proportional to T, the graph of νm versus T will be a straight line with a positive slope. This means that if we were to plot the frequency (ν) on the y-axis and temperature (T) on the x-axis, we would expect a linear graph.
Based on the understanding that the graph must be linear with a positive slope, we can identify the correct option from the given choices. The option that represents a linear graph with a positive slope is the correct answer.
The correct option for the v-T graph for the spectral distribution of radiance in a perfectly black body is the one that shows a linear relationship with a positive slope.
Similar Questions
Knowledge Check
Which of the following I-V graph represents ohmic conductors?
A B
B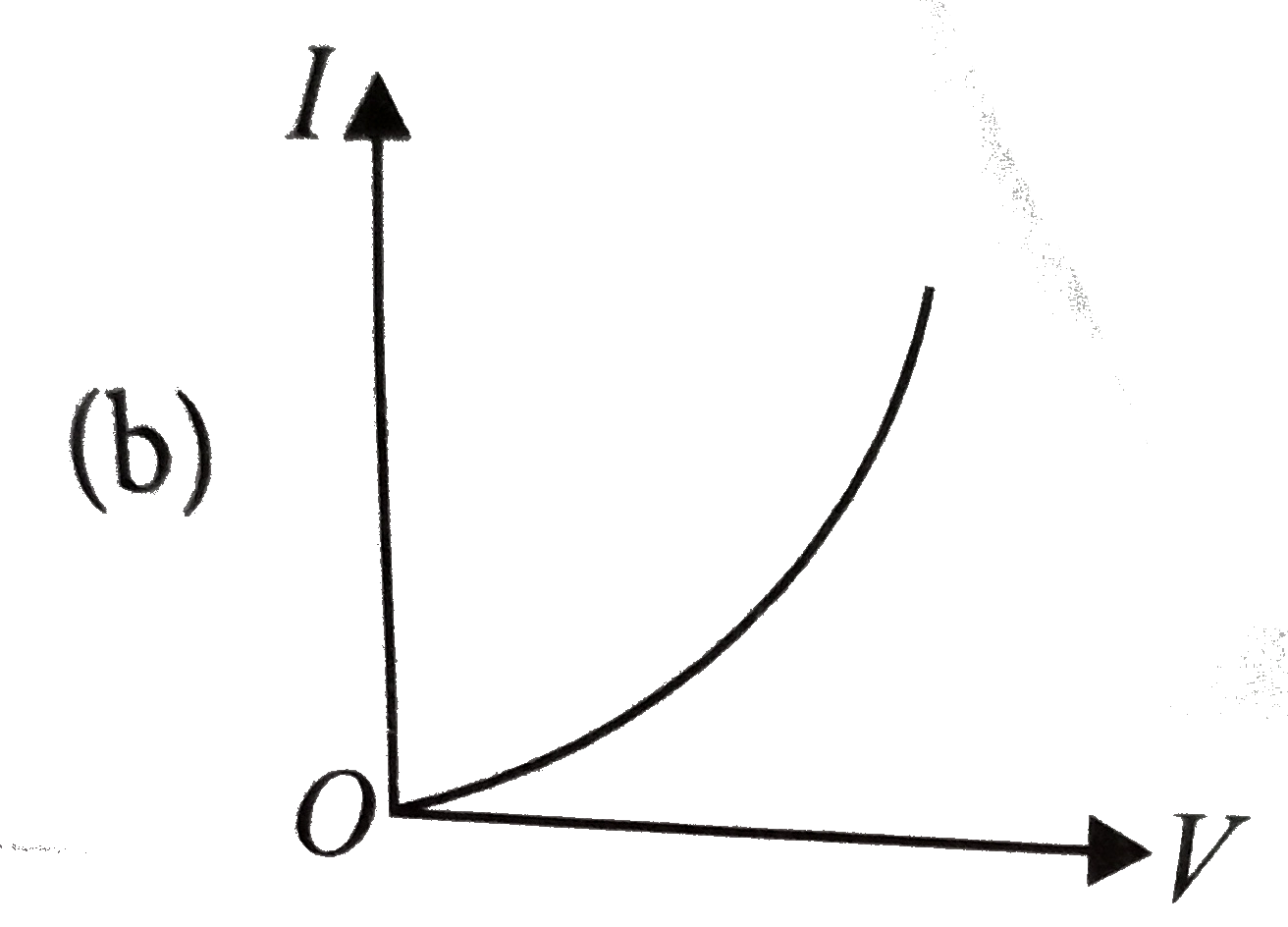 C
C D
D
Which of the following is correct for V-I graph of a good conductor?
A B
B C
C D
D
Which of the following is the vm = T graph for a perfectly black body ( vm =maximum frequency of radiation)
 AABBCCDD
AABBCCDD
Which of the following speed - time (v - t) graphs is physically not possible?
View SolutionWhich of the following graph ploltted between P and V is
INCORRECT ?
View SolutionName the law which helps us to explain the distribution of energy in the spectrum of a black body for
(i) short wavelength only (ii) long wavelength only.
View SolutionWhich of the following graph(s) represent retardation ? [v : velocity, t : time, x : position]
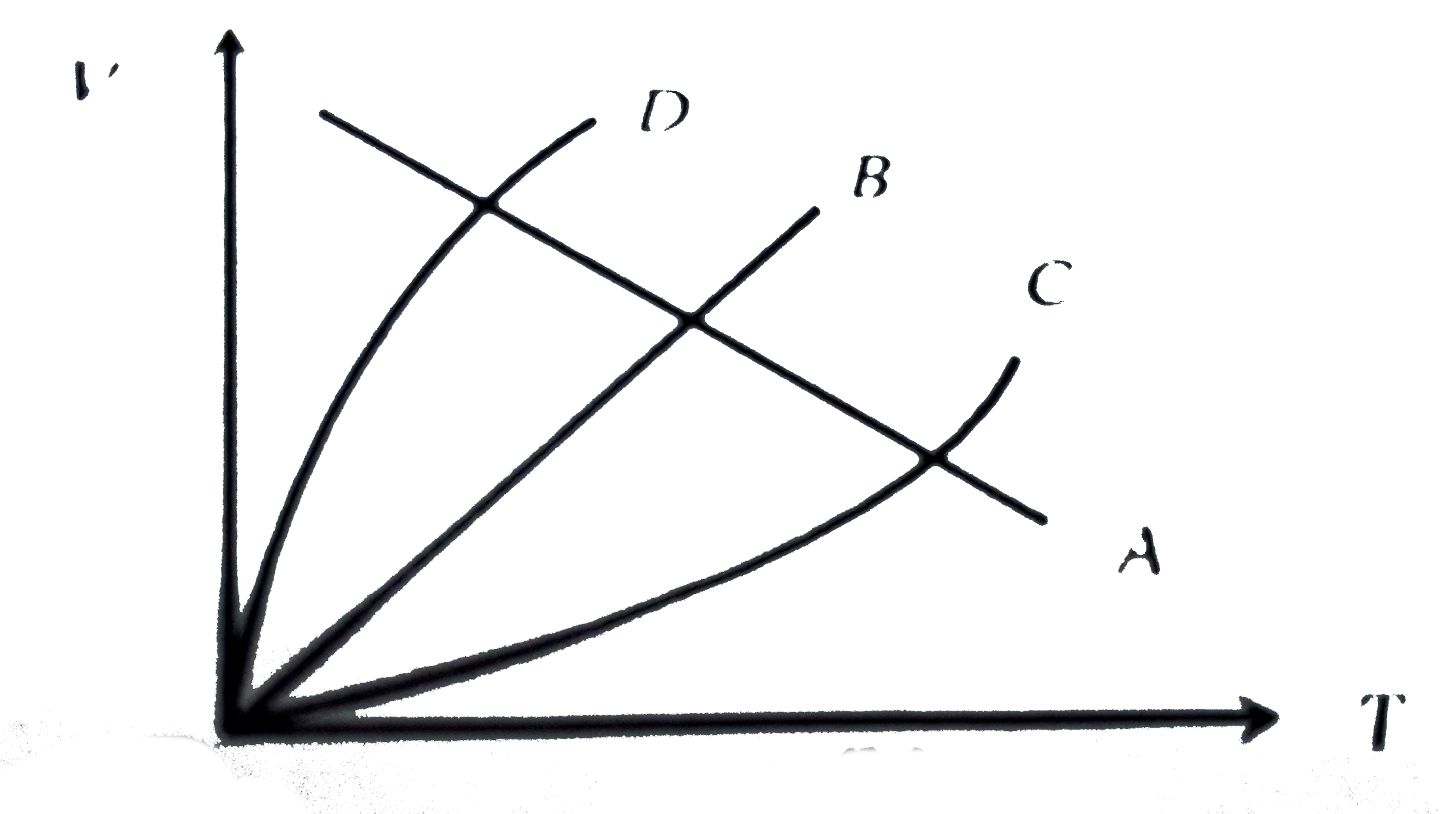
View Solutionwhich of the following volume temperature (V−T) graph represent carnot engine cycle ABCDA?
View Solution