An inductor coil is connected to an source through a 60Ω resistance in series. The source voltage, voltage across the coil and voltage across the resistance are found to be 33V, 27V and 12V respectively. The resistance of the coil is
A. 30Ω
B. 45Ω
C. 105Ω
D. 75Ω
30Ω
45Ω
105Ω
75Ω
The correct Answer is:B
To find the resistance of the inductor coil, we can follow these steps:
Step 1: Identify the given values
- Source voltage (V_s) = 33V
- Voltage across the coil (V_L) = 27V
- Voltage across the resistance (V_R) = 12V
- Resistance in series (R_s) = 60Ω
Step 2: Calculate the current in the circuit
Using Ohm's law, the current (I) can be calculated using the voltage across the resistance:
I=VRRs=12V60Ω=0.2A
Step 3: Apply the voltage equation for the circuit
According to Kirchhoff's voltage law, the total voltage in the circuit is equal to the sum of the voltages across the coil and the resistance:
Vs=VL+VR
Step 4: Substitute the known values into the equation
Substituting the known values into the equation:
33V=27V+12V
This confirms that the voltage values are consistent.
Step 5: Use the relationship between voltages to find the resistance of the coil
We know that:
VL=I⋅RL
Where RL is the resistance of the coil. Rearranging gives:
RL=VLI=27V0.2A=135Ω
Step 6: Calculate the total resistance in the circuit
The total resistance in the circuit is the sum of the series resistance and the coil resistance:
Rtotal=Rs+RL
Step 7: Rearranging to find the coil resistance
We can rearrange to find the resistance of the coil:
RL=Rtotal−Rs
Step 8: Calculate the total resistance
Using the total voltage and current:
Rtotal=VsI=33V0.2A=165Ω
Step 9: Substitute to find the coil resistance
Now substituting back to find RL:
RL=165Ω−60Ω=105Ω
Conclusion
The resistance of the coil is 105Ω.
- Source voltage (V_s) = 33V
- Voltage across the coil (V_L) = 27V
- Voltage across the resistance (V_R) = 12V
- Resistance in series (R_s) = 60Ω
Using Ohm's law, the current (I) can be calculated using the voltage across the resistance:
According to Kirchhoff's voltage law, the total voltage in the circuit is equal to the sum of the voltages across the coil and the resistance:
Substituting the known values into the equation:
We know that:
The total resistance in the circuit is the sum of the series resistance and the coil resistance:
We can rearrange to find the resistance of the coil:
Using the total voltage and current:
Now substituting back to find RL:
The resistance of the coil is 105Ω.
Similar Questions
If the voltage across 500Ω is 5 V. then R2 is
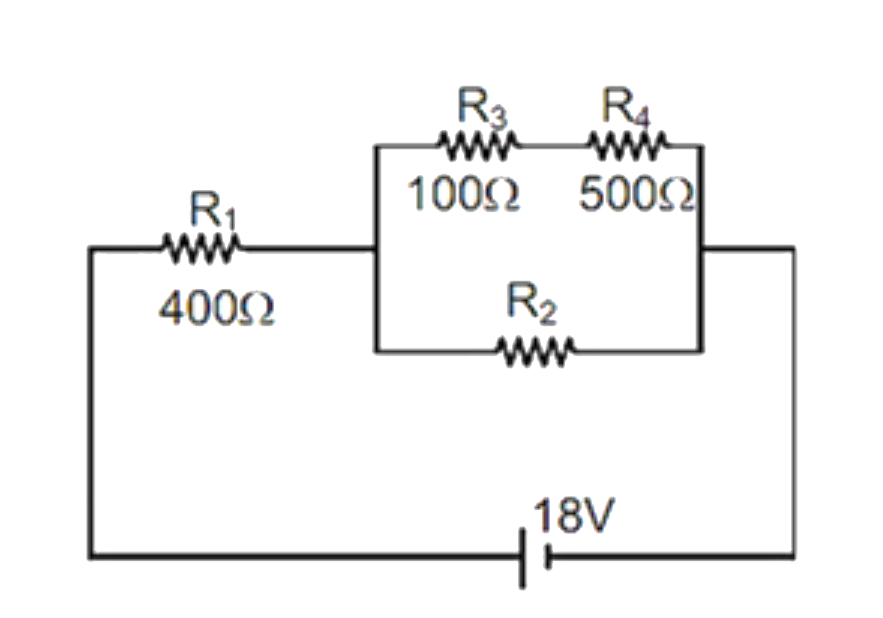 View Solution
View SolutionIn series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View SolutionA coil of negligible resistance is connected inseries with 90Ω resistor acorss a 120 V -60 Hz line. A voltmeter reads 36 V across the resistance. Find voltage across the coil and inductance of the coil.
View SolutionA 20volts AC is applied to a circuit consisting of a resistance and a coil with negligible resistance. If the voltage across the resistance is 12V, the voltage across the coil is
View SolutionIf a wire of resistance 20Ω is covered with ice and a voltage of 210V is applied across the wire , then the rate of melting of ice is
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?View SolutionAn alternating voltage is connected in series with a resistance R and inductance L if the potential drop across the resistance is 200V and across the inductance is 150V, then the applied voltage is
View SolutionA 1250 W heater operates at 115V. What is the resistance of the heating coil?
View SolutionA 1250 W heater operates at 115V. What is the resistance of the heating coil?
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
Calculate the value of the resistor R, for the proper working of the lamp.View Solution

