Shown in the figure is a circular loop of radius, r and resistance R. A variable magnetic field of induction is established inside the coil. If the key (K) is closed at t=0 , the electrical power developed at the instant is equal to
The correct Answer is:D
To solve the problem, we need to find the electrical power developed at the instant when the key K is closed at t=0. We will follow these steps:
Step 1: Determine the Magnetic Flux
The magnetic field B is given as:
B=e−t
The area A of the circular loop with radius r is:
A=πr2
Thus, the magnetic flux Φ through the loop is given by:
Φ=B⋅A=B⋅πr2=e−t⋅πr2
Step 2: Find the Induced EMF
According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) E is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for Φ:
E=−ddt(e−t⋅πr2)
Using the product rule, we differentiate:
E=−πr2⋅ddt(e−t)=−πr2⋅(−e−t)=πr2e−t
Step 3: Calculate the Power Developed
The electrical power P developed in the circuit is given by:
P=E2R
Substituting the expression for E:
P=(πr2e−t)2R=π2r4e−2tR
Step 4: Evaluate at t=0
Now we evaluate the power at t=0:
P(t=0)=π2r4e0R=π2r4R
Final Answer
Thus, the electrical power developed at the instant when the key is closed is:
P=π2r4R
---
The magnetic field B is given as:
B=e−t
The area A of the circular loop with radius r is:
A=πr2
Thus, the magnetic flux Φ through the loop is given by:
Φ=B⋅A=B⋅πr2=e−t⋅πr2
According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF) E is given by the negative rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for Φ:
E=−ddt(e−t⋅πr2)
Using the product rule, we differentiate:
E=−πr2⋅ddt(e−t)=−πr2⋅(−e−t)=πr2e−t
The electrical power P developed in the circuit is given by:
P=E2R
Substituting the expression for E:
P=(πr2e−t)2R=π2r4e−2tR
Now we evaluate the power at t=0:
P(t=0)=π2r4e0R=π2r4R
Thus, the electrical power developed at the instant when the key is closed is:
P=π2r4R
Similar Questions
In the circuit shown the key (K) is closed at t=0, the current through the key at the instant t=10−3ln,2 is

View SolutionA conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionA uniform circular loop of radius a and resistance R is pulled at a constant velocity v out of a region of a uniform plane of the loop and the velocity are both perpendicular to B. Then the electrical power in the circular loop at the instant when the arc (of the circular loop) outside the region of magnetic field subtends an angle π3 at the centre of the loop is
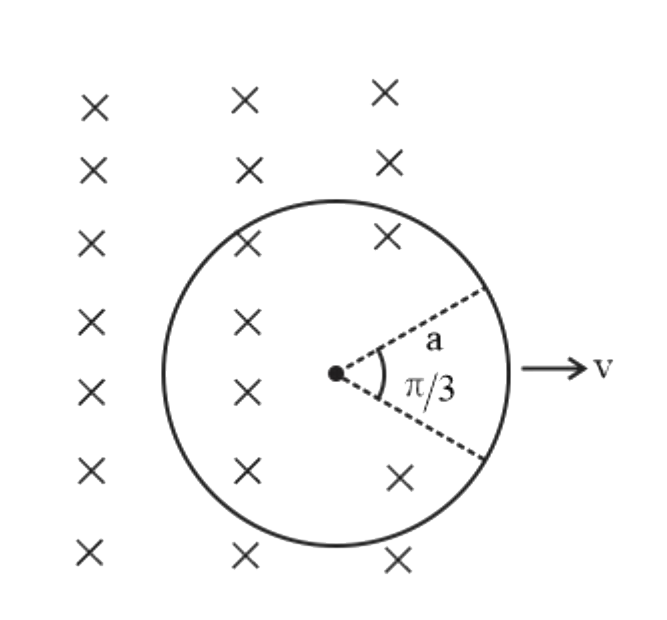
View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is

View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View Solution
